Classifying with k-Nearest Neighbors（k近邻）

终于要开始写自己的第一篇博客啦，真有点小激动（手足无措 =。=！）。因为最近正在琢磨机器学习，第一篇博客就从学的第一个算法开始：k-nearest neighbors algorithm即k近邻算法。

**************************************正文分界线***************************************

据wiki：在模式识别和机器学习领域，k近邻算法（k-nearest neighbors algorithm or k-NN for short）是应用于分类问题（classification ）和回归问题（regression）的一种无参数方法。分类时，k-NN输出为所属分类（class membership）；回归时，k-NN输出为属性值（property value）。

分类（classification），即识别出样本所属的类别。因为还没学到regression，所以只写classification（是只会好嘛，TAT）

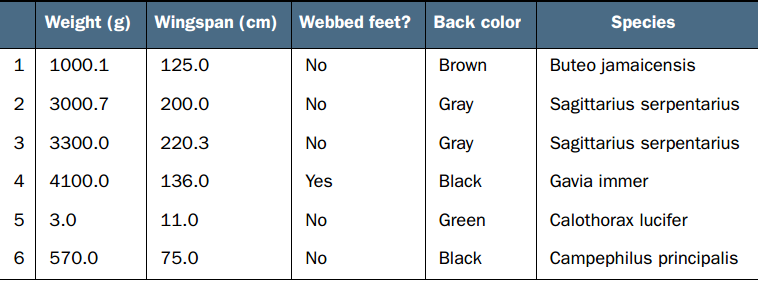
首先，看一下数据的形式，比如下图“基于四种特征对鸟进行分类 ”

kNN算法

给定训练样本集（training set），我们知道其中每条数据的label（即所属类别，比如什么鸟）。关注两个key words：特征（feature）和目标变量（target variable），每条数据均看成“特征向量+目标变量”（比如[weight, wingspan, ..., ...]+species）的形式，在这里，数据的label即目标变量。当没有label的新数据“特征向量+？”到来时，我们将它和训练样本集中的每条数据进行比对，计算他们特征向量间的距离（相似程度的度量），挑选训练样本集中k个与之距离最近的数据，观察他们的label并计数，即进行“投票表决”，票数最高的label是新数据的label（分类，并不一定正确）。

General approach to kNN

1. Collect data : Any method, such as a text file provided or a database.

2. Prepare : Numeric values are needed for a distance calculation. A structured data format is best.

3. Analyze : Any method, for example, using Matplotlib to make 2D plots of data.

4. Train : Does not apply to the kNN algorithm. No explicit training step is required.

5. Test : Calculate the error rate(=error number/dataset size) with a test set.

6. Use: This application needs to get some input data and output structured numeric values. Next, the application runs the kNN algorithm on this input data and determines  which  class  the  input  data  should  belong  to.  The  application  then takes some action on the calculated class.

Pros: High accuracy, insensitive to outliers, no assumptions about data

Cons: Computationally expensive, requires a lot of memory

Works with: Numeric values, nominal values

以下几点需要注意

1. 因为需要计算距离，所以特征应为数字型，比如weight和wingspan，像webbed feet这样的布尔型或者back color这样的字符串型的就不能使用；

2. 因为特征的单位和数值范围（scale）不同，所以要对特征进行归一化，均压缩至0至1或-1至1

3. 距离不一定是欧氏距离（Euclidean distance），也可以是其他定义（范数）

4. 每次classify都要遍历整个样本集，当样本集很大和特征向量很长时，计算成本和内存成本“高昂”

代码实现要点

1. 将数据组织成我们需要的形式（函数实现），特征向量以行的形式“堆砌”成矩阵（matrix或2d array），相应的目标变量排成一列形成向量（list）

2. 使用python的dict数据结构用于“计票”很方便，以label为“键”（key），以票数为“值”（value），然后以value排序提取key即可

重要思想

1. 将样本看成“特征向量+目标变量”的形式

2. 数据结构的巧妙运用

参考

[1] Harrington, Peter. Machine learning in action. Manning Publications Co., 2012.

[2] http://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm#cite_note-1

来自为知笔记(Wiz)