2186 Popular Cows

Popular Cows

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 41771		Accepted: 16955

Description

Every cow's dream is to become the most popular cow in the herd. In a herd of N (1 <= N <= 10,000) cows, you are given up to M (1 <= M <= 50,000) ordered pairs of the form (A, B) that tell you that cow A thinks that cow B is popular. Since popularity is transitive, if A thinks B is popular and B thinks C is popular, then A will also think that C is 
popular, even if this is not explicitly specified by an ordered pair in the input. Your task is to compute the number of cows that are considered popular by every other cow. 

Input

* Line 1: Two space-separated integers, N and M

* Lines 2..1+M: Two space-separated numbers A and B, meaning that A thinks B is popular.

Output

* Line 1: A single integer that is the number of cows who are considered popular by every other cow. 

Sample Input

3 3
1 2
2 1
2 3

Sample Output

1

Hint

Cow 3 is the only cow of high popularity. 

Source

USACO 2003 Fall

 

 

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

 

在此题 要求被其他所有的牛崇拜的牛的数量 例如 

1 崇拜2

2 崇拜3

3 崇拜2

那么答案就是2 ,   2和3马被其它所有的节点崇拜, 是一个强连通分量

 

学习了这个博客

https://www.cnblogs.com/shadowland/p/5872257.html

再Tarjan算法中，有如下定义。

DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

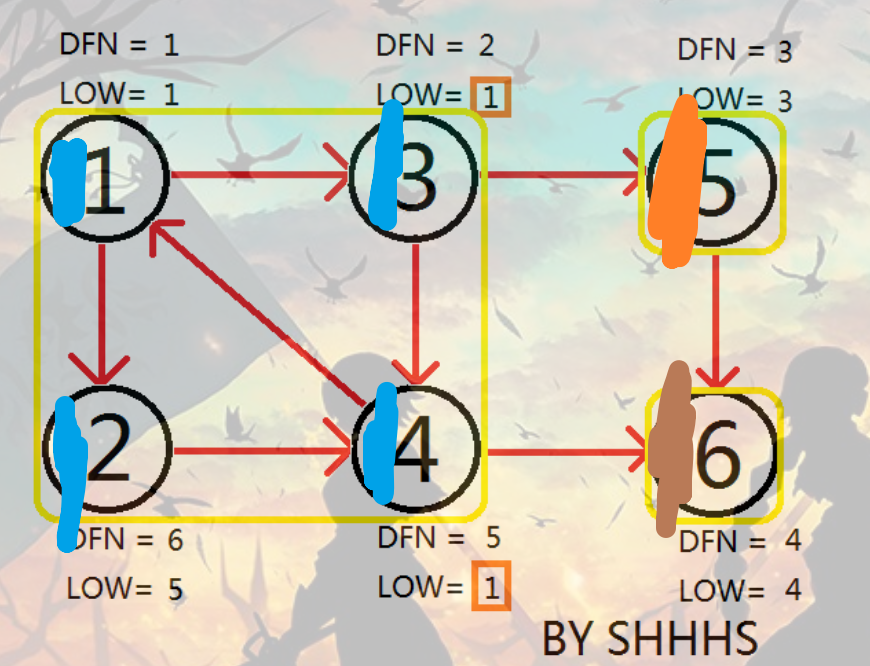
觉得叫color好点 给节点染色 有多少种颜色就有多少个强连通分量 同种颜色的节点处于同一个强连通分量

借这个图说明一下染色

为了打字 以下缩写DFN=LOW为条件

首先DFS 栈里面有1 3 5 6

到第六个节点  已经到达DFS最深处 满足条件 染成棕色 栈里面有1 3 5

返回到5 满足条件 染成橙色 栈里面有1 3

到3

再到4 4可以到1  但是不满足!dfn[v] ,  它满足!color[v], low[id] = min(low[id], dfn[v]); low[4] = 1, 不满足条件 栈里面有 1 3 4

回到3 low[id] = min(low[id], low[v]); low[3] = 1, 不满足条件 栈里面有 1 3 4

到1

再到2 2可以到4  但是不满足!dfn[v] ,  它满足!color[v], low[id] = min(low[id], dfn[v]); low[2] = 5, 不满足条件 栈里面有 1 3 4 2

再回到1 满足条件 把栈里面的都拿出来染成蓝色 完毕

注意要反向建图(是这样子叫么?)

#include <stdio.h>
#include <iostream>
#include <vector>
#include <algorithm>
int N, M;
using namespace std;

const int si = 10010;
vector<int> G[si];
int dfn[si], low[si], color[si], size[si], stk[si];
bool flag[si];

int timelag, colorcnt, stksize;
void tarjan(int id) {
	dfn[id] = low[id] = ++timelag;
	stk[stksize++] = id;
	for (int i = 0; i < G[id].size(); i++) {
		int v = G[id][i];
		if (!dfn[v]) {//dfn也是vis的标志 是否来过
			tarjan(v);
			low[id] = min(low[id], low[v]);
		}
		else if (!color[v]) {
			low[id] = min(low[id], dfn[v]);
		}
	}
	if (dfn[id] == low[id]) {//染色
		int cnt = 0;
		colorcnt++;
		while (stksize) {
			stksize--;
			int x = stk[stksize];
			color[x] = colorcnt;
			cnt++;
			if (x == id) break;
		}
		size[colorcnt] = cnt;
	}
}
int main() {
	cin >> N >> M;
	while (M--) {
		int a, b;
		scanf("%d %d", &a, &b);
		G[b].push_back(a);//反向建图
	}
	for (int i = 1; i <= N; i++) {
		if (!dfn[i]) tarjan(i);//求强连通分量 dfn也是vis的标志
	}

	for (int i = 1; i <= N; i++) {
		for (int j = 0; j < G[i].size(); j++) {
			int x = G[i][j];//i到x的边 但是他们不是同一个颜色的 上图的3和5是这种关系
			if (color[i] != color[x]) flag[color[x]] = 1;
			//x崇拜i 则x所处的强连通分量都崇拜i 所有与x颜色相同的都崇拜i
			//但是i不崇拜x 否则i和x是同一个强连通分量同一种颜色了 所以扩大到整个x的颜色
		}
	}
	int num = 0, ans = 0;
	for (int i = 1; i <= colorcnt; i++) {
		if (flag[i]) continue;
		num++;
		ans = size[i];
	}
	if (num != 1) ans = 0;//只会有一个被其它所有牛崇拜的强连通分量
	cout << ans << endl;
	return 0;
}