清北澡堂 Day 3 上午

1.数论函数的卷积公式

(ƒ*g)(n)=Σ_d|nƒ(d)×g(n/d)

已知f*[1~n]，g[1~n]

怎么求(f*g)[1~n]?

　　一个个求复杂度O(n根号n)

如何加速？

　　考虑更换枚举顺序（这点很重要，在接下来的一些求和运算中会用到）

　　枚举代码：

ll f[N],g[N],h[N];
void calc(int n)
{
    for(int i=;i*i<=n;i++)
    {
        h[i*j]+=f[i]*g[i];
        for(int j=i+;i*j<=n;j++)
            h[i*j]+=f[i]*g[j]+f[j]*g[i];
    }
}

这样子速度就会变为n log n

例子1：

求当a≤x≤b，c≤y≤d时，gcd(x,y)=1的个数

前缀和如图

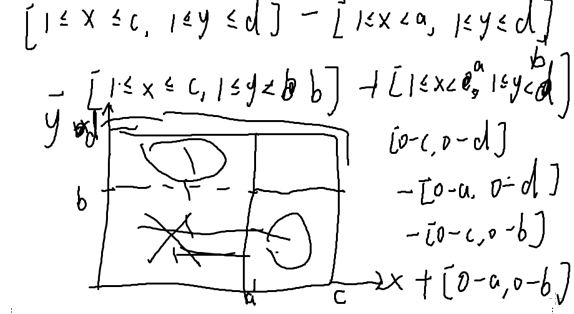
式子为：

Σ_i=1ⁿ Σ_j=1^m [gcd(i,j)=1]

　　[]意思：为真返回1否则返回0

　　联系到莫比乌斯函数μ(d)

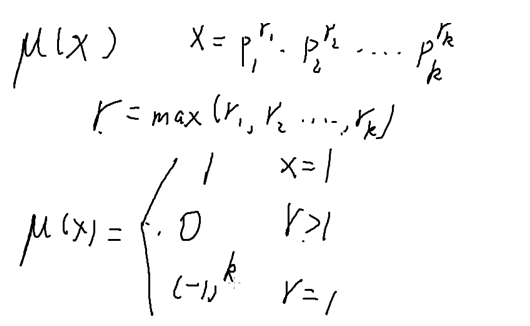
　　Σ_d|n μ(d)：

　　　　当n=1时它=1

　　　　否则=0

这两个是可以等效替换的：

Σ_i=1ⁿ Σ_j=1^m Σ_d|gcd(i,j)μ(d)

交换枚举顺序，降到了线性复杂度:

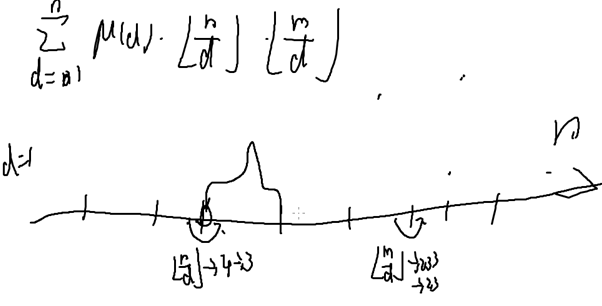
对于这个东西：

d从1枚举到n时，可能的取值只有o（根号n）种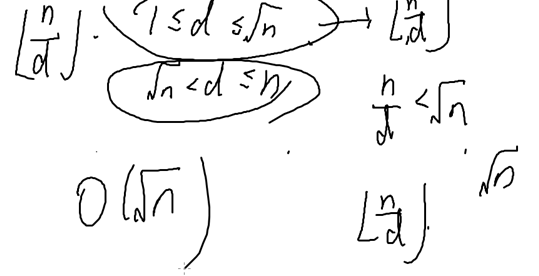

由于当1≤d≤根号n和根号n≤d≤n时，最多情况数都是根号n

所以可能的取值为O(根号n)种

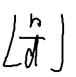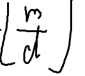我们可以画一条数轴，每一个节点表示或者的值有变化，则我们可以画出O(根号n)个区间    ，并且复杂度O(根号n)

可以推出x的表达式：

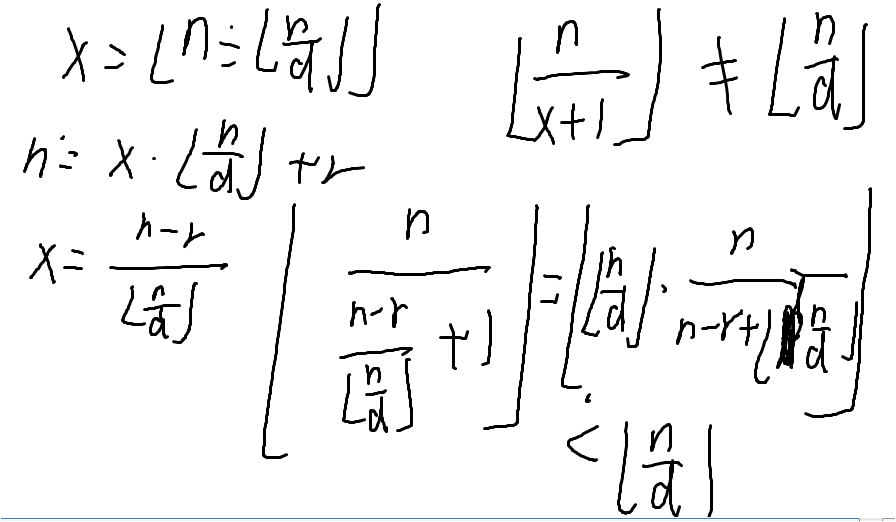
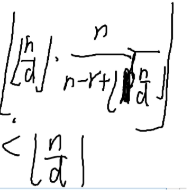这里是因为这部分要＜n，

所以这个分数是＜1的，一个整数乘一个＜1的数再取整，所得的数小于原来的整数

代码：

 xian_xing_shai();

 for (int a=;a<=n;a++)
     sum_mu[a] = sum_mu[a-] + mu[a];

 int solve(int n,int m)
 {
     int ans=;
     //for (int d=1;d<=n;d++)
     //    ans += mu[d] * (n/d) * (m/d);
     for (int d=;d<=n;)
     {
         int next_d = min(
             n/(n/d),
             m/(m/d)
         );
         ans += (sum_mu[next_d] - sum_mu[d-]) * (n/d) * (m/d);
         d=next_d+;
     }
     return ans;
 }

例子2
求当a≤x≤b,c≤y≤d时gcd(x,y)是质数的(x,y)的个数

交换枚举顺序：变为枚举质数P在前

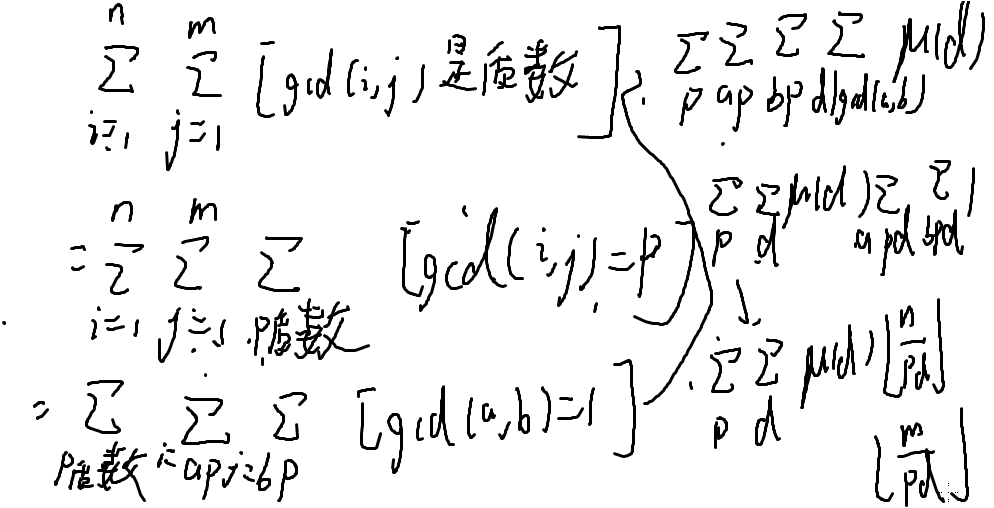
然后再变换枚举的东西：

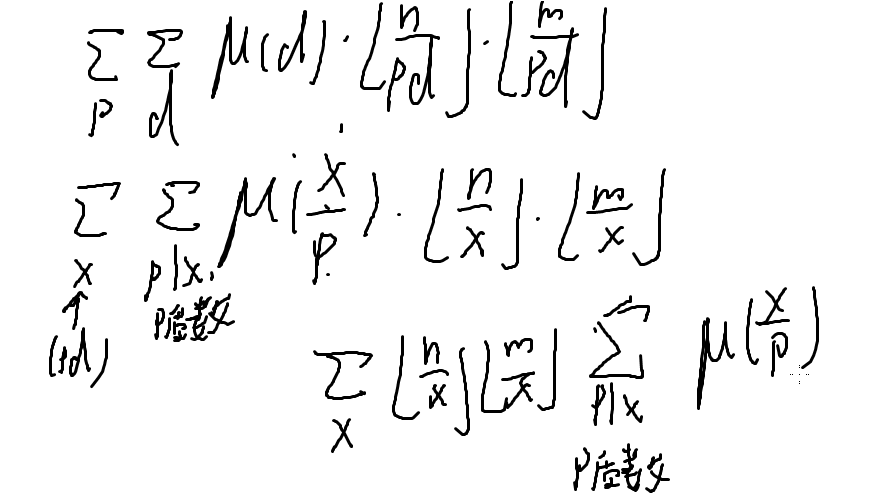
这个东西是一个积性函数，可以按照积性函数求

2.组合数问题

一.加法原理：具有性质A的事件有m个，具有性质B的事件有n个，则具有性质A或性质B的事件有m+n个

百度百科定义：做一件事情，完成它有n类方式，第一类方式有M1种方法，第二类方式有M2种方法，……，第n类方式有Mn种方法，那么完成这件事情共有M1+M2+……+Mn种方法。

举个例子：从武汉到上海有乘火车、飞机、轮船3种交通方式可供选择，而火车、飞机、轮船分别有k1，k2，k3个班次，那么从武汉到上海共有 k1+k2+k3种方式可以到达。

二，乘法原理：具有性质A的事件有m个，具有性质B的事件有n个，则具有性质A及性质B的事件有mn个

百度百科定义：做一件事，完成它需要分成n个步骤，做第一 步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法。那么完成这件事共有 N=m1×m2×m3×…×mn种不同的方法。

例如，从A城到B城中间必须经过C城，从A城到C城共有3条路线（设为a，b，c），从C城到B城共有2条路线（设为m，t），那么，从A城到B城共有3×2=6条路线

对于每一个质因数的n次方，共有n+1中选择方法，即这个质因数的0~n次方

故共有   4*3*5=60  种方法

 

取两册文字不同的书的方案=取日文英文+取日文中文+取英文中文

相同的：取日文日文，取中文中文，取英文英文

随便取两册：上两问加起来

排列组合：

组合：

从n个元素中选取r个元素，当不计顺序时，其方案数为：

C_n^r=C(n,r)=n!/r!(n-r)!  

排列：

从n个元素中选取r个元素，当考虑顺序时，其方案数为：

P_n^r=P(n,r)=n! / (n-r)!

考虑两面旗帜的方法和三盆花的方法，根据乘法原理乘起来即可

ans=P(5,2)*P(20,3)

先考虑对七名男生排序，然后在六个间隔中插入三名女生

ans=P(7,7)*P(6,3)

 

先看个位数：有0，2，4，6，8五种情况，对于0和8，它的千位数都是有2,3,4,5,6五种情况，对于剩下的三个数，各有2,3,4,5,6中除去它自己四种情况，故千位和个位可能的情况共有：2*5+4*3=22 种 ，然后对百位和十位排序，有P(8,2)种情况

故ans=22*P(8,2)

总的方案数减去选上男A和女B的方案数

ans=C(12,5)-C(10,3)

按余数分类：余数相同和余数不同

余数相同分为：(0,0,0),(1,1,1).(2,2,2);

1~300这些数中，余数相同的各有100个

故每一种可能的方式均为C(100,3)

余数不同时，每一个数都是从不同的余数中选一个，故方式为C(100,1)³

ans=3*C(100,3)+C(100,1)³

由于每种颜色的旗帜是相同的，所以讲相同颜色的旗帜放一起，只能算是一种方式

这个时候我们需要用组合数

ans=C(16,4)*C(12,4)*C(8,4)*C(4,4);（为什么楼主也在想...有待补充，哪位大佬会记得跟我说一下）

组合数及其相关性质

• 有n个不同元素，从中选r个，但是每个可以选多次，则其方案数为C(n+r-1,r)

证：设选的数为a1,a2,....,ar，（由小到大），则1≤a₁≤a₂≤a₃......≤a_r≤n

我们可以通过一种变换，就是让ai+i-1，这样可以去掉=

有：1≤a₁<a₂+1<a₃+2<.....<a_r+r-1<n-r+1

中间还是有r个数，我们可以设b_i=a_i+i-1

则1≤b₁<b₂<b₃<....<b_r≤n-r+1

所以问题就开始转换为无重复组合问题，即在n+r-1 个元素中选中 r个的组合数 。

• 有n个不同元素，从中选r个，但是选中的元素大小不能相邻，则其方案数为C(n-r+1,r)

证：设选的数为a1,a2,....,ar，（由小到大），则1<a₁<a₂<a₃<......<a_r<n\

其中a₁+1<a₂，a₂+1<a₃....

将每个a_i-i+1

有a₁<a₂-1<a₃-2<...<a_r-r+1

其他的一些性质

• C(n+m,n)=C(n+m,m)
• C(n,m)=C(n-1,m-1)+C(n-1,m)
• C(n+r+1,r)=C(n+r,r)+C(n+r-1,r-1)+C(n+r-2,r-2)+....+C(n,0)
• C(n,l)C(l,r)=C(n,r)C(n-r,l-r)
• C(n,0)+C(n,1)+.....+C(n,n)=2ⁿ
• C(n,0)-C(n,1)+C(n,2)-...=0
• C(r,r)+C(r+1,r)+...+C(n,r)=C(n+1,r+1)