栈与后缀表达式C实现

 #include<stdio.h>
 #include<stdlib.h>

 typedef char datatype;
 typedef struct stack
 {
     int top;                     /*栈顶指针*/
     datatype* data;              /*数组*/
     int MaxSize;                    /*栈大小*/
 }stack;

 /*初始化空栈*/
 void InitStack(stack* st, int sz)
 {
     st->top = -;
     st->MaxSize = sz;
     st->data = (datatype*)malloc(sizeof(datatype) * st->MaxSize);                   //分配内存
 }
 /*释放站空间*/
 void FreeStack(stack* st)
 {
     free(st->data);
 }
 /*压栈*/
 int Push(stack* st, datatype d)
 {
     if (st->top == st->MaxSize-) return -;
     st->data[++(st->top)] = d;
     return ;
 }
 /*弹栈*/
 datatype Pop(stack* st)
 {
     if ((st->top) == -)
     {
         printf("llll%d",st->top);
         exit(-);
     }
     else {
         return st->data[(st->top)--];
     }

 }
 /*取顶*/
 datatype getTop(stack* st)
 {
     if(st->top>-)
         return st->data[st->top];
     return NULL;
 }
 /*栈置空*/
 void MakeEmpty(stack* st)
 {
     st->top = -;
 }

 /*后缀表达式计算*/
 int Midcal()
 {
     stack* sptr = (stack*)malloc(sizeof(stack));
     char buf[];
     int i = , k;
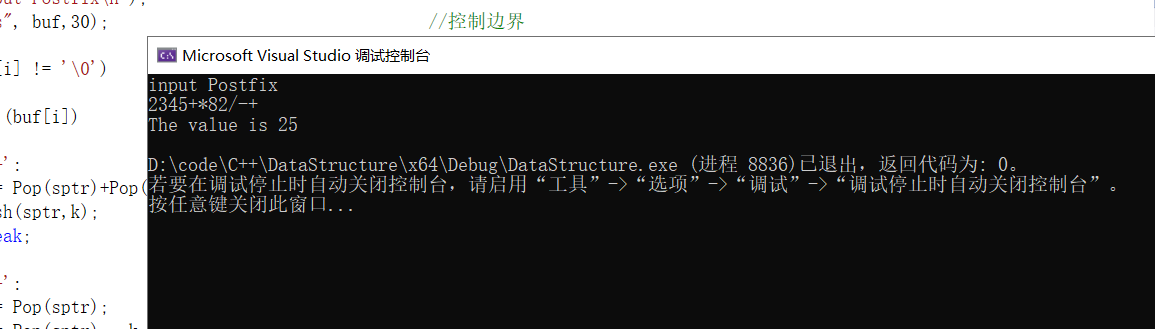
     InitStack(sptr, );

     printf("input Postfix\n");
     scanf_s("%s", buf,);                                 //控制边界

     while (buf[i] != '\0')
     {
         switch (buf[i])
         {
         case '+':
             k = Pop(sptr)+Pop(sptr);
             Push(sptr,k);
             break;

         case '-':
             k = Pop(sptr);
             k = Pop(sptr) - k;
             Push(sptr, k);
             break;
         case '*':
             k = Pop(sptr) * Pop(sptr);
             Push(sptr, k);
             break;

         case '/':
             k = Pop(sptr);
             k = Pop(sptr) / k;
             Push(sptr, k);
             break;
         default:

             Push(sptr, (int)(buf[i] - ));
         }
         i++;
     }
     printf("The value is %d\n", Pop(sptr));
     return ;
 }

 main() {
     Midcal();
 }

注：我们在使用scan方法时建议使用scanf_s: 因为这个方法有溢出限制和边界检查，防止因数据溢出造成程序数据混乱的问题。

　　其中VS2019以及接近版本都会在使用scanf时报错，强制使用scanf_s.

scanf_s("%type",space,limit)  第一个参数是类型，第二个参数是输入数的存储地址，第三个就是你的限制空间了。

　　以上代码部分，如果设置limit <10,就会出现错误，限制小于输入时，超出部分不会进行读取。