[Leetcode][动态规划] 第935题 骑士拨号器

一、题目描述

国际象棋中的骑士可以按下图所示进行移动：

                         

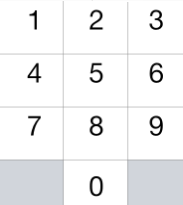
我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。

每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。

你能用这种方式拨出多少个不同的号码？

因为答案可能很大，所以输出答案模 10^9 + 7。

示例 1：

输入：1
输出：10

示例 2：

输入：2
输出：20

示例 3：

输入：3
输出：46

二、题目分析

1）动态规划。状态定义：dp[i][j]代表从j开始跳i步的可能性
2）辅助条件：建立一个map<int,vector<int>>,代表谁经过一步能跳到j位置

3）初始化dp[0][0-9]=1;

4）状态转移：dp[i][j]+=dp[i-1][mp[j][k]],0<=k<=mp[j].size()-1;

5）结果：sum(dp[n-1][0-9])

三、代码实现

class Solution {
public:
    int knightDialer(int N) {
        if (!N)return ;
        vector <vector<int>>dp(N, vector<int>());
        int i, j, k;
        int Max = pow(, ) + ;
        for (i = ; i < ; ++i) {
            dp[][i] = ;
        }
        map<int, vector<int>>mp;
        mp.insert({ ,{ , } }), mp.insert({ ,{ , } }), mp.insert({ ,{ , } }), mp.insert({ ,{ , } }), mp.insert({ ,{ ,, } });
        mp.insert({ ,{} }), mp.insert({ ,{ ,, } }), mp.insert({ ,{ , } }), mp.insert({ ,{ ,, } }), mp.insert({ ,{ , } });
        for (i = ; i < N; ++i) {
            for (j = ; j <= ; ++j) {
                for (k = ; k < mp[j].size(); ++k) {
                    dp[i][j] += dp[i - ][mp[j][k]];
                    if (dp[i][j] > Max)
                        dp[i][j] = dp[i][j] % Max;
                }
            }
        }
        int sum = ;
        for (int i = ; i <=; ++i) {
            sum += dp[N - ][i];
            if (sum > Max)sum %= Max;
        }
        return sum;
    }
};