embedding技术

目录

• word2vec
• 负采样
  • 目标函数
  • 反向梯度
• 层次softmax
  • NPLM的目标函数和反向梯度
  • 目标函数
  • 反向梯度
• GNN(图神经网络)
  • deepwalk
  • node2vec
• 附录

word2vec

Word2Vec是一个可以将语言中的字词转换为低维、稠密、连续的向量表达（Vector Respresentations）的模型,其主要依赖的假设是Distributional Hypothesis(1954年由Harris提出分布假说,即上下文相似的词，其语义也相似；我的理解就是词的语义可以根据其上下文计算得出)

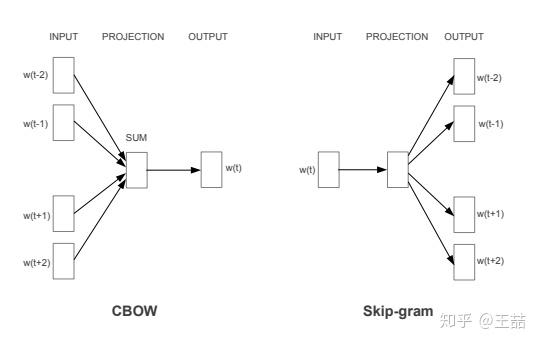
Word2vec主要分为CBOW(Continuous Bag of Words)和Skip Gram两种模式，其中CBOW是从原始数据推测目标字词；而Skip-Gram是从目标字词推测原始语句，其中CBOW对小型数据比较合适，而Skip-Gram在大型预料中表现得更好。

负采样

负采样的基本思想是用采样一些负例的方式近似代替遍历整个词汇。

目标函数

$ J^h( \theta ) = log \sigma( \Delta S_{\theta}(w,h)) + k log(1 - \sigma(\Delta S_{\theta}(w,h))) $
\(其中h=w_1,...,w_n为上下文词序列\)
\(P_n(w)代表负样本分布为,w是抽样词\)
\(P_d(w)代表正样本(真实数据)分布\)
$ \sigma(x)=\frac{1}{1+e^{-x}}是sigmoid函数 $
$ \theta 代表模型参数$
\(k 代表负样本与正样本的比例\)
\(P^h( D=1|w,\theta ) = \frac{P^h_{\theta}(w)}{P^h_{\theta}(w)+kP_n(w)}=\sigma(\Delta S_{\theta}(w,h)) 代表在给定上下文h,参数\theta情况下w是正样本的概率\)
\(其中S_{\theta}(w,h)=\hat{q}(h)^T q_w + b_w = (\sum^n_{i=1}c_i \bigodot r_{w_i})^T q_w + b_w\)
\(\hat{q}(h) = \sum^n_{i=1}c_i \bigodot r_{w_i}是上下文词向量的线性加权,代表对目标词的估计值\)
\(c_i代表上下文词在位置i的权重向量\)
\(r_{w_i}代表上下文词i的词向量表示\)
\(q_w代表目标词的词向量表示\)
\(b_w代表上下文无关的偏置项\)

反向梯度

$ \frac{\partial }{\partial \theta} J^{h,w}(\theta) = (1-\sigma(\Delta S_{\theta}(w,h))) \frac{\partial }{\partial \theta}logP^h_\theta(w) - \sum^k_{i=1}[\sigma(\Delta S_{\theta}(w,h))\frac{\partial }{\partial \theta}logP^h_\theta(x_i)]$

公式中使用k个噪音样本的词向量加和来代替词典全部词汇的加和,所以NCE的训练时间只线性相关于负样本个数,与词典大小无关。

层次softmax

Hierarchical Softmax中不更新每个词的输出词向量，更新的是二叉树(哈夫曼树)上节点对应的向量。代价由