C++ 洛谷 2014 选课 from_树形DP

洛谷 2014 选课

没学树形DP的，看一下。

首先要学会多叉树转二叉树。

树有很多种，二叉树是一种人人喜欢的数据结构，简单而且规则。
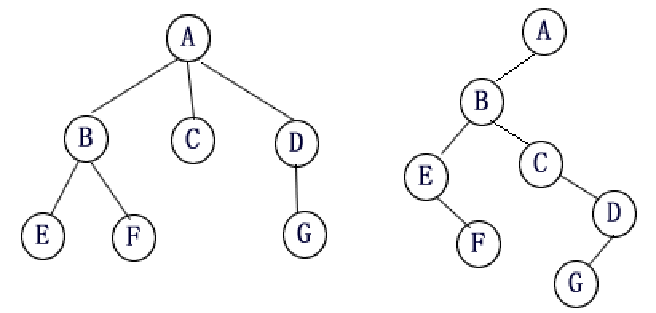
但一般来说,树形动规的题目很少出现二叉树,因此将多叉树转成二叉树就是一种必备的手段，方法非常简单,“左儿子,右兄弟” 。
就是将一个节点的第一个儿子放在左儿子的位置，下一个儿子，即左儿子的第一个兄弟,放在左儿子的右儿子位置上，再下一个兄弟接着放在右儿子的右儿子，以此类推。

代码：

scanf("%d%d",&u,&v)  //v的父亲是u
if(l[u]==) l[u]=v;      //多叉树转二叉树  如果u没有儿子，则v作u的儿子
else r[v]=l[u];         //如果u有儿子，则为上一个儿子l[u]的兄弟
l[u]=v;                   //刷新l[u]，作为下一个兄弟的“父亲”

为什么要这样转二叉，等会你就知道了。(好神秘)

分析：以样例为例，课程之间关系如下图：

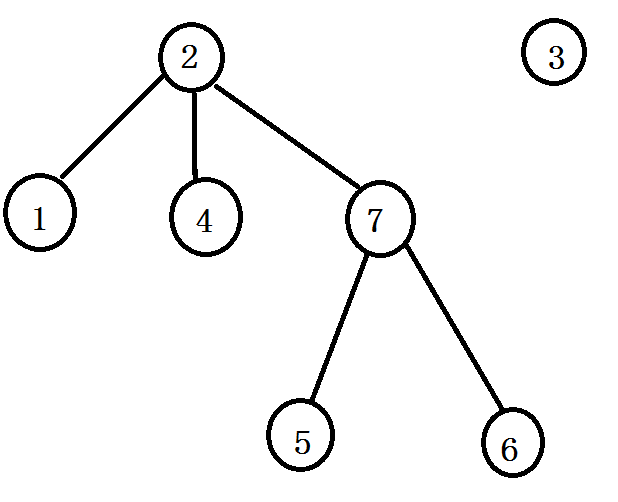 转换为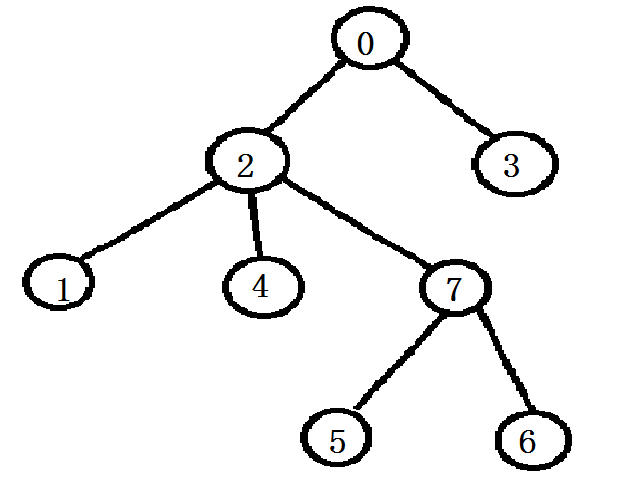  

在转化后的二叉树上，我们如果选第1，就必须先选2，如果选3，不一定要选2。

设dp[i][j]表示选到第i门课，还要选j门课的最大学分，那么分两种情况讨论：

如果选i，则还要在l[i]上选k门，并且在r[i]上选就j-k-1门。

如果不选i，则只能在r[i]上选j门，0<=k<j。

现在你知道这种转二叉树的好处了吧。

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=;
int n,m;
int k,s[maxn];
int last[maxn],l[maxn],r[maxn],vis[maxn][maxn];
int end;
int f[maxn][maxn];
int tree_f(int x,int sum)                 //动归方程
{
       if(!sum||x==-) return ;
       if(vis[x][sum]!=) return f[x][sum];
       int minn=-<<;
       vis[x][sum]=;
       minn=max(minn,tree_f(r[x],sum));           //不选i，就只能在右子树上选sum门。
       for (int i=;i<=sum-;i++)
       minn=max(minn,tree_f(l[x],i)+tree_f(r[x],sum-i-)+s[x]);   //选i，左子树上选i门，右子树上选sum-i-1门。
       f[x][sum]=minn;
       return minn;
}
void work()
{
    memset(l,-,sizeof(l));
    memset(r,-,sizeof(r));
    memset(f,-,sizeof(f));
    scanf("%d%d",&n,&m);
    for (int i=;i<=n;i++)
    {
    scanf("%d%d",&k,&s[i]);
    if(l[k]==) l[k]=i;      //多叉树转二叉树
    else r[i]=l[k];
    l[k]=i;
    }
    printf("%d",tree_f(,m+));
}
int main()
{
    work();
    return ;
}