Codeforces Gym101205D：Fibonacci Words（KMP+递推）

Gym 101205D

题意：f[0] = "0", f[1] = "1"，接下来f[i] = f[i-1] + f[i-2]，相当于字符串拼接。然后给出一个n和一个串s，问f[n]里面有多少个s。

思路：在int范围内的f[n]是n=31的时候，但是匹配的s的长度只有1e5，这时候n=27刚好大于它，因此可以先求解出n<=27的串的情况，然后由这些串来得到n>27的时候的情况。

比赛的时候想着递归算，结果爆栈。

看别人的代码之后我的理解是这样的：

(1)当n<=28的时候，可以直接kmp算。

(2)当n>28的时候，我们可以得到下面的递推式：(ans[i]表示f[i]里面有多少个s.可以先kmp求出ans[i](25 <= i <= 28) ).

先定义odd = ans[27] - ans[26] - ans[25]（即得到s[27]由s[26]和s[25]拼接起来的时候能多得到的答案）.

even = ans[28] - ans[27] - ans[26]（即得到s[28]由s[27]和s[26]拼接起来的时候能多得到的答案）.

因为len(s[27])和len(s[28])一定大于匹配的s，因此不用每次都暴力求解拼接起来的时候能多得到的答案，只需要在i为奇数的时候加上odd，i为偶数的时候加上even就可以得到拼接起来能多得到的答案了。

一开始以为奇偶是一样的情况，但是WA8之后问别人才知道是不一样的。

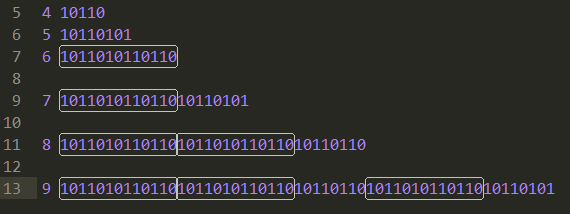
找6号串和找5号串的情况，可以发现6号串可以出现在8号串连接处而不能出现在7和9号串连接处。5号串能出现在7和9号的连接处但是不能出现在8号串的连接处，所以应当是分开考虑的。

这就是WF最水的题目之一...

 #include <bits/stdc++.h>
 using namespace std;
 #define N 105
 #define M 100010
 typedef long long LL;
 int nxt[M], len[N], sz;
 string str, s[N];
 LL ans[N];

 void Make_Next() {
     int i, j; j = nxt[] = -; i = ;
     while(i < sz) {
         while(j != - && str[i] != str[j]) j = nxt[j];
         if(str[++i] == str[++j]) nxt[i] = nxt[j];
         else nxt[i] = j;
     }
 }

 LL Kmp(int id) {
     int i = , j = , ans = ;
     while(i < len[id]) {
         while(- != j && s[id][i] != str[j]) j = nxt[j];
         i++; j++;
         if(j >= sz) { ans++; j = nxt[j]; }
     }
     return ans;
 }

 int main() {
     int n, cas = ;
     s[] = "", s[] = ""; len[] = len[] = ;
     for(int i = ; i <= ; i++) s[i] = s[i-] + s[i-], len[i] = len[i-] + len[i-];
     while(~scanf("%d", &n)) {
         cin >> str;
         sz = str.length(); Make_Next();
         if(n <= ) { printf("Case %d: %lld\n", cas++, Kmp(n)); continue; }
         for(int i = ; i <= ; i++) ans[i] = Kmp(i);
         LL odd = ans[] - ans[] - ans[], eve = ans[] - ans[] - ans[]; // 拼接起来能够得到的贡献
         for(int i = ; i <= n; i++) {
             ans[i] = ans[i-] + ans[i-];
             if(i & ) ans[i] += odd;
             else ans[i] += eve;
         }
         printf("Case %d: %lld\n", cas++, ans[n]);
     }
     return ;
 }