关于DFS的理解

DFS(深度优先搜索)相当于暴力寻找有效解的过程

如果把多种情况写成一个树的方式

那么DFS的实质就是遍历所有分枝来寻找最优解

而DFS中遍历所有解的方式采用了我们称之为回溯法的东西

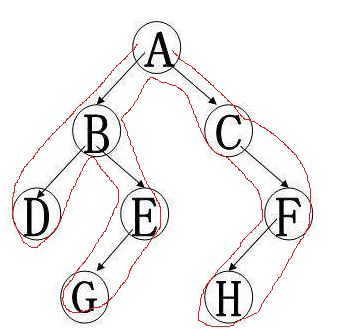
如图所示

图中的搜索顺序为从A到B到D

然后在向回退一步

此时原来D的地方因为被访问过

所以不选择访问之

选择访问E，之后访问G

因为E和G被访问过

所以我们需要往回走到A

此时向C开始访问

具体过程很好理解

做题时只需要每一次判断下是否满足条件即可

下面上@Armin 给我们写的关于DFS相当好的模板

想看@Armin 博客的同学请点击左边的友链哦

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------

 void dfs(int )
 {
     if(到达终点状态)
     {
         ...//根据题意添加
         return;
     }

     for(所有方式)
     {
         if(扩展方式所达到状态合法)
         {
             修改操作;//根据题意来添加
             标记;//访问过这个元素
             dfs();
             还原标记;
             //是否还原标记根据题意
             //如果加上就是回溯法
         }
     }
 }

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------

关于回溯法的话主要还是根据题意

如果题意仅仅要求判断是否有解的话

就没有必要再去回溯了

浪费时间

Notes:其实因为DFS是一个递归的过程

其实还真的不是那么好懂

博主整整看了两天才差不多理解

有疑问的欢迎在评论区留言

01:27:21　　2018-11-20　　Author:LanceYu