csp联考T1

---

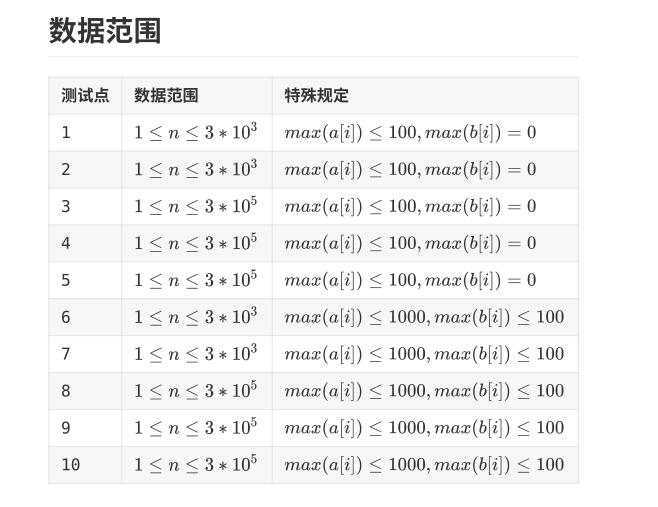
本题主要难点在于如何处理dist^2的问题

40分算法

n^2暴力就不必多嘴，直接枚举根节点DFS就行了。

---

70分算法

对于b=0的情况，我们可以考虑用换根法来计算根节点的变化对总权值带来的影响。

换根法一般的处理步骤是先以1为根处理出一些信息，然后根据这些信息再做一次DFS。

那这道题要维护哪些信息呢？

考虑换根时都有哪些变了：假设根节点从u变到v,显然，v及v的子树的贡献都会-dist(u,v)

,其他节点的贡献会+dist(u,v）。所以，总的权值变化就是dist(u,v)*(a[v子树外的点]-a[子树内的点]）

随便搞搞就好

100分正解

对于b，我们可以如法炮制。对于一次换根（u->v）:

对于v子树的点：设原距离为x,则贡献从bx^{2变为b*(x-dist(u,v))}2

两式相减，可得变化量为b(dist(u,v)^{2-2x*dist(u,v))。同理，子树外的点的变化量为b*(dist(u,v)}2+2xdist(u,v))。

加到一起，总变化量就是sumbdist(u,v)^2+2dist(u,v)(xb[v子树外的点]-x*b[子树内的点]）。

维护下必要的信息就好。

#include<bits/stdc++.h>
using namespace std;
#define re register ll
#define F(x,y,z) for(re x=y;x<=z;x++)
#define FOR(x,y,z) for(re x=y;x>=z;x--)
#define I inline void
#define IN inline ll
typedef long long ll;
I read(ll &res){
    re g=1;register char ch=getchar();res=0;
    while(!isdigit(ch)){
        if(ch=='-')g=-1;
        ch=getchar();
    }
    while(isdigit(ch)){
        res=(res<<3)+(res<<1)+(ch^48);
        ch=getchar();
    }
    res*=g;
}
struct E{
    int to,nt;
}e[606000];
#define T e[k].to
ll n,m,head[303000],S,ans,tot=-1,X,Y,suma,sumb,t[303000],siz[303000],a[303000],b[303000],f[303000],g[303000],A[303000],B[303000];
I D_1(ll x,ll fa){
    A[x]=a[x];B[x]=b[x];f[x]=0;siz[x]=1;t[x]=0;
    for(re k=head[x];k!=-1;k=e[k].nt){
        if(T==fa)continue;
        D_1(T,x);siz[x]+=siz[T];
        A[x]+=A[T];B[x]+=B[T];f[x]+=f[T]+siz[T];t[x]+=(t[T]+B[T]);
    }
}
I D_2(ll x,ll fa,ll sum,ll dis){
    g[x]=sum;S+=(a[x]*dis)+(b[x]*dis*dis);
    for(re k=head[x];k!=-1;k=e[k].nt){
        if(T==fa)continue;
        D_2(T,x,sum+n-siz[T]-siz[T],dis+1);
    }
}
I D_3(ll x,ll fa,ll sum,ll num){
    //cout<<"!"<<x<<" "<<sum<<" "<<num<<endl;
    ans=max(ans,sum);
    for(re k=head[x];k!=-1;k=e[k].nt){
        if(T==fa)continue;
        D_3(T,x,sum+suma-A[T]-A[T]+sumb+2ll*(num+(t[x]-t[T]-B[T]))-2ll*(t[T]+B[T]),num+t[x]-t[T]-B[T]+sumb-B[T]);
    }
}
int main(){
    //freopen("T1.in","r",stdin);
    //freopen("T1.out","w",stdout);
    read(n);
    memset(head,-1,sizeof(head));
    suma=sumb=0;
    F(i,1,n){
        read(a[i]);suma+=a[i];
    }
    F(i,1,n){
        read(b[i]);sumb+=b[i];
    }
    F(i,1,n-1){
        read(X);read(Y);
        e[++tot].to=Y;
        e[tot].nt=head[X];
        head[X]=tot;
        e[++tot].to=X;
        e[tot].nt=head[Y];
        head[Y]=tot;
    }
    D_1(1,0);
    S=0ll;
    D_2(1,0,f[1],0);
    D_3(1,0,S,0);
    //F(i,1,n){
        //cout<<i<<":"<<f[i]<<" "<<g[i]<<" "<<A[i]<<" "<<B[i]<<" "<<t[i]<<endl;
    //}
    printf("%lld",ans);
    return 0;
}