「SNOI2019」积木

传送门

Description

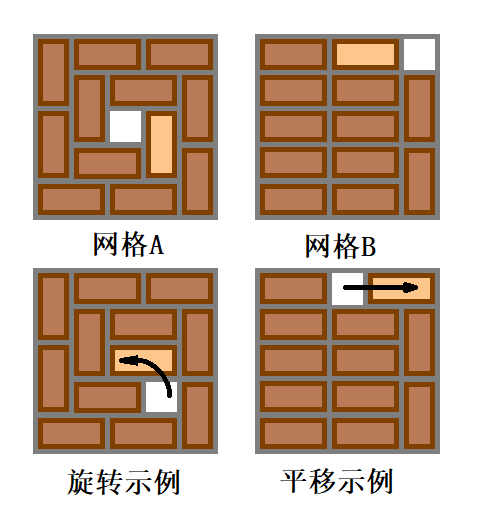
有一块\(n\)行\(m\)列的网格板， \(n,m\)都是奇数。网格上平铺着一些\(1*2\)的积木。积木可以旋转，不能重叠。网格板上只有一格的空位。

你可以做两种操作：

1. 将一块与空白格相邻（指有公共边）的积木旋转\(90^{\circ}\)到空白格中；
2. 将一块与空白格相邻的积木平移至空白格中。

如图所示（被移动的积木颜色较浅）：

请你用以上两种操作将给定的网格板变换为指定的状态。

Solution 

发现并没有要求用最短的步骤（笑。。。

其实，每次改变空格的位置的同时，都可以顺便使得目标状态中这个空格位置的木块归位

移着移着，就移到目标状态中的空格的位置了

但是此时我们只能保证移动路线上的木块都归位了，所以我们需要dfs，如果碰到不合法就使其归位，这样的移动路径必然会是一个环，所以我们又回到了最初不合法的位置

每个格子只需被搜索一次，因为搜索完某个格子后，它的木块必然已经归位了。

原来是大模拟啊

Code 

#include<bits/stdc++.h>
#define dbg1(x) cerr<<#x<<"="<<(x)<<" "
#define dbg2(x) cerr<<#x<<"="<<(x)<<"\n"
#define dbg3(x) cerr<<#x<<"\n"
#define ll long long
using namespace std;
#define reg register
const int MN=2005;
const int tr[4][2]={{0,2},{1,3},{2,0},{3,1}};
const int dx[4]={0,-1,0,1},dy[4]={-1,0,1,0};
const char ch[4]={'L','U','R','D'};
int N,M,x,y,xp,yp,len;
char a[MN][MN],c[(MN*MN)<<1];
int ta[MN][MN],tb[MN][MN];
bool vis[MN][MN];

void init(int (*ts)[MN],int &_x,int &_y)
{
	reg int i,j;
	for(i=1;i<=N;++i) scanf("%s",a[i]+1);
	for(i=1;i<=N;++i)for(j=1;j<=M;++j)
		switch(a[i][j])
		{
			case 'o':_x=i,_y=j;ts[i][j]=-1;break;
			case '<':ts[i][j]=2;break;
			case '>':ts[i][j]=0;break;
			case 'n':ts[i][j]=3;break;
			case 'u':ts[i][j]=1;break;
		}
}
void one_step(int k)
{
	c[len++]=ch[k];
	int xi=x+dx[k],yi=y+dy[k];
	int xj=xi+dx[ta[xi][yi]],yj=yi+dy[ta[xi][yi]];
	ta[x][y]=tr[k][0];ta[xi][yi]=tr[k][1];
	ta[x=xj][y=yj]=-1;
}

void Walk_to_o(int X,int Y)
{
	while((x^X)||(y^Y))
		one_step(tb[x][y]);
}

void dfs(int X,int Y)
{
	if(vis[X][Y]) return;
	vis[X][Y]=true;
	for(int i=0;i<4;++i)
	{
		int xi=X+dx[i],yi=Y+dy[i];
		if(xi>N||xi<1||yi<1||yi>M||vis[xi][yi]) continue;
		int xj=xi+dx[tb[xi][yi]],yj=yi+dy[tb[xi][yi]];

		if(ta[xi][yi]^tb[xi][yi])
			one_step(i),Walk_to_o(xj,yj),one_step(tb[xj][yj]);
		one_step(i);
		vis[xi][yi]=true;
		dfs(xj,yj);
		one_step(tb[xj][yj]);
	}
}

int main()
{
	scanf("%d%d",&N,&M);
	init(ta,x,y);init(tb,xp,yp);

	Walk_to_o(xp,yp);

	dfs(xp,yp);
	return 0*printf("%s\n",c);
}

---

Blog来自PaperCloud，未经允许，请勿转载，TKS！