偶数矩阵 Even Parity,UVa 11464

题目描述 Description

给你一个n*n的01矩阵（每个元素非0即1），你的任务是把尽量少的0变成1，使得每个元素的上、下、左、右的元素（如果存在的话）之和均为偶数。如图所示的矩阵至少要把3个0变成1，最终如图所示，才能保证其为偶数矩阵。

 输入输出格式 Input/output

输入格式：
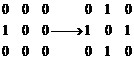
输入的第一行为数据组数T（T<30）。每组数据的第一行为正整数n（1 < n < 15）；接下来的n行每行包含n个非0即1的整数，相邻整数间用一个空格隔开。
输出格式：
对于每组数据，输出被改变的元素的最小个数。如果无解，应输出-1。

 输入输出样例 Sample input/output

样例测试点#1

输入样例：

0 0 0

1 0 0

0 0 0

输出样例：

3

 

思路：这道题很经典，经典的枚举也有DP的意味在里面，这里我把书上的思路详细化。

书上谈到：抛弃枚举每个数字的方法，这样很大，大概2²⁵⁵这么多的情况，很大，难以接受，可以考虑枚举第一行，这样有2¹⁵种可能，是可行的，根据第一行算出第二行，以此类推到第n行，时间复杂度降为O(2ⁿ×n²)

点石成金罢了，下面来说说如何具体的做到：

将样例的第一行：

0 0 0

可以通过枚举变成

0 1 0

这样第一行就确定下来了，这时候考虑第二行：

0 1 0

α

考虑一下第一行第一列的0，它的上下左右加和=α+1，那么这时候要保证是偶数，即(α+1)%2==0，所以α=1，这时候看看这个α可不可以由原矩阵A的这个位置的数变化而来（即0→1），合法，此时记上1。

0 1 0

1 α

同样计算第一行第二列，(0+α+0)%2==0，α=0，比较原矩阵，合法，记上0。

0 1 0

1 0 α

同上，合法变换矩阵为：

0 1 0

1 0 1

最终执行完：

0 1 0

1 0 1

0 1 0

 

大致的思路就是这样，要注意的是一些细节之处，比如位运算简化，这样可以使代码简洁很多且运算方便

 

代码如下（书上copy下来且加了点注释的）：

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>
 #include <math.h>
 const int MAXN=;
 const int INF=;
 int A[MAXN][MAXN],B[MAXN][MAXN];
 int n;
 int min(int a,int b)
 {
     return a>b?b:a;
 }
 int check(int s)
 {
     memset(B,,sizeof(int));
     for(int c=;c<n;c++)//枚举第一行
     {
         if(s&(<<c)) B[][c]=;
         else if(A[][c]==) return INF;//不能把1变成0，直接返回
     }
     for(int r=;r<n;r++)//从第二行开始依次筛查
     {
         for(int c=;c<n;c++)
         {
             int sum=;//表示上左右三个元素的和
             if(r>) sum+=B[r-][c];
             if(c>) sum+=B[r-][c-];
             if(c<n-) sum+=B[r-][c+];
             B[r][c]=sum%;
             if(A[r][c]==&&B[r][c]==) return INF;//违法，不能把1变为0
         }
     }
     int cnt=;
     for(int r=;r<n;r++)
     {
         for(int c=;c<n;c++)
         {
             if(A[r][c]!=B[r][c]) cnt++;
         }
     }
     return cnt;
 }
 int main()
 {
     int r,c;//行、列
     int i,j;
     int T;
     int ans=INF;//初始化为最大值
     scanf("%d",&T);
     while(T)
     {
         ans=INF;
         scanf("%d",&n);
         for(i=;i<n;i++)
         {
             for(j=;j<n;j++)
             {
                 scanf("%d",&A[i][j]);
             }
         }
         for(int s=;s<(<<n);s++)//1<<n等于2^n，不用pow，比较方便
         {
             ans=min(ans,check(s));//不断更新最小ans
         }
         if(ans==INF) ans=-;//没找到答案
         printf("%d %d\n",T,ans);
         T--;
     }
     return ;
 }