ubuntu之路——day9.1 深度学习超参数的调优

参数重要性：

第一阶：α即learning rate

第二阶：momentum中的β，hidden units的数量，mini-batch的大小

第三阶：hidden layers的数量，learning rate decay的参数

参数选择的方式：

一、完全在一定范围内进行随机

二、尝试完毕上述随机参数后，以粗糙到精确的思路，缩小随机范围并重复第一步

python中参数的具体实现：

对于学习率α而言：0 < α < 1

所以打个比方如果测试 0.0001 ≤ α ≤ 1显然这是一种指数分布，如果直接随机数那么90%的可能性都会取到[0.1,1]之间，只有10%的资源会去测试[0.001,0.1]这显然是不合理的，所以使用以下方法

r = -4 * np.random.rand() 此时会随机出一系列[-4,0]区间的数

α = 10^r即可

对于动量梯度下降法momentu中的β而言：假设 0.9 < β < 0.999

我们知道1/1-β就是β平均的范围，比如取0.9的时候它就平均了10天内的温度，取0.999它就平均了1000天内的温度

所以实质上我们是在取1-β在[0.1,0.001]上的取值

因此r的范围就是[-1,-3]

1-β = 10^r

β = 1-10^r

迭代模型的过程：感谢吴恩达老师的公开课，以下图片均来自吴恩达老师的课件

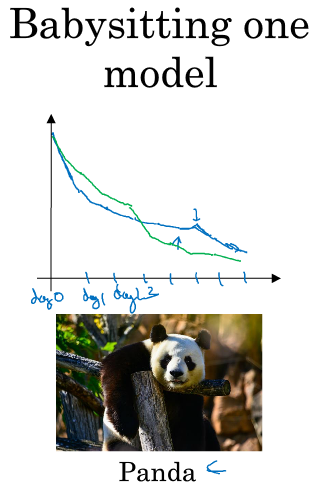
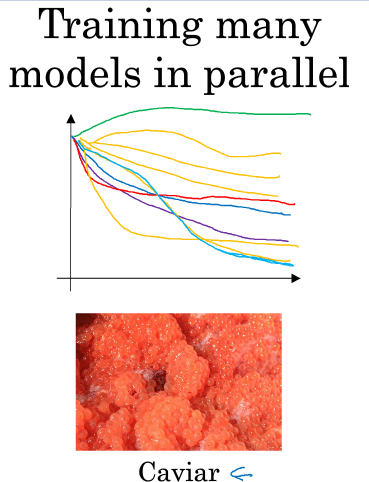
前者是一次训练一个模型，并每天在这个模型的基础上进行优化直到这个模型收敛到一定精度，适用于计算资源有限且数据量较大的环境

后者是一次训练多个模型，在多个模型中直接找到较为优秀的模型然后再进行优化，适用于有海量算力的环境