[POJ1189][BZOJ1867][CODEVS1709]钉子和小球

题目描述 Description

有一个三角形木板,竖直立放，上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每个格子的宽度也都等于d，且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。 
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2），且球的中心还会正对着下一颗将要碰上的钉子。例如图2就是小球一条可能的路径。 
我们知道小球落在第i个格子中的概率pi=pi=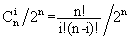，其中i为格子的编号，从左至右依次为0,1,...,n。 
现在的问题是计算拔掉某些钉子后，小球落在编号为m的格子中的概率pm。假定最下面一排钉子不会被拔掉。例如图3是某些钉子被拔掉后小球一条可能的路径。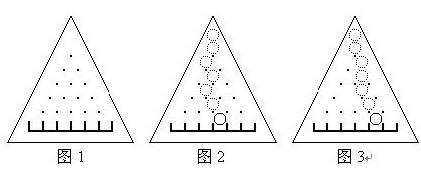 

输入描述 Input Description

第1行为整数n（2 <= n <= 50）和m（0 <= m <= n）。以下n行依次为木板上从上至下n行钉子的信息，每行中'*'表示钉子还在，'.'表示钉子被拔去，注意在这n行中空格符可能出现在任何位置。

输出描述 Output Description

仅一行，是一个既约分数(0写成0/1)，为小球落在编号为m的格子中的概pm。既约分数的定义：A/B是既约分数，当且仅当A、B为正整数且A和B没有大于1的公因子。

样例输入 Sample Input

5 2
    *
   * .
  * * *
 * . * *
* * * * *

样例输出 Sample Output

7/16

数据范围及提示 Data Size & Hint

之前的一些废话：还有两天出国

题解：概率DP，f(i,j)表示到了第i行第j列的概率，首先f(1,1)=1,然后对于每一个钉子，各有50%的几率掉到左右两个块，转移为f(i+1,j+1)+=f(i,j)/2,f(i+1,j)+=f(i,j)/2，对于把钉子拆了的情况，可以理解成小球直接往下掉了两行，不进行往两边的转移。

比较坑爹的是，这题要输出既约分数，我刚开始写了一个分数的结构体，但是发现RE不断，后来用DP数组只存了分子，然后就A了。还有一个比较坑的是BZOJ不让输出回车，要不然presentation_error.

代码：

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
typedef long long LL;
#define mem(a,b) memset(a,b,sizeof(a))
typedef pair<int,int> PII;
inline int read()
{
    int x=,f=;char c=getchar();
    while(!isdigit(c)){if(c=='-')f=-;c=getchar();}
    while(isdigit(c)){x=x*+c-'';c=getchar();}
    return x*f;
}
LL gcd(LL a,LL b){return b==0ll ? a : gcd(b,a%b);}
int n,m,len[];
LL dp[][];
char s[];
bool pic[][];
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++)for(int j=;j<=i;j++)
    {
        scanf("%s",s);
        if(s[]=='*')pic[i][j]=;
    }
    dp[][]=;
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
        {
            if(!pic[i][j] && i!=n){dp[i+][j+]=4ll*dp[i][j];continue;}
            dp[i+][j]=dp[i+][j]+dp[i][j];
            dp[i+][j+]=dp[i+][j+]+dp[i][j];
        }
    LL a=dp[n+][m+],b=1ll<<n,t=gcd(a,b);
    if(a==)printf("0/1");
    else printf("%lld/%lld",a/t,b/t);
    return ;
}

总结：不要轻易的打分数结构体。