图论之最短路算法之SPFA算法

SPFA（Shortest Path Faster Algorithm）算法，是一种求最短路的算法。

SPFA的思路及写法和BFS有相同的地方，我就举一道例题（洛谷——P3371 【模板】单源最短路径（弱化版）来做讲解吧！

如题：



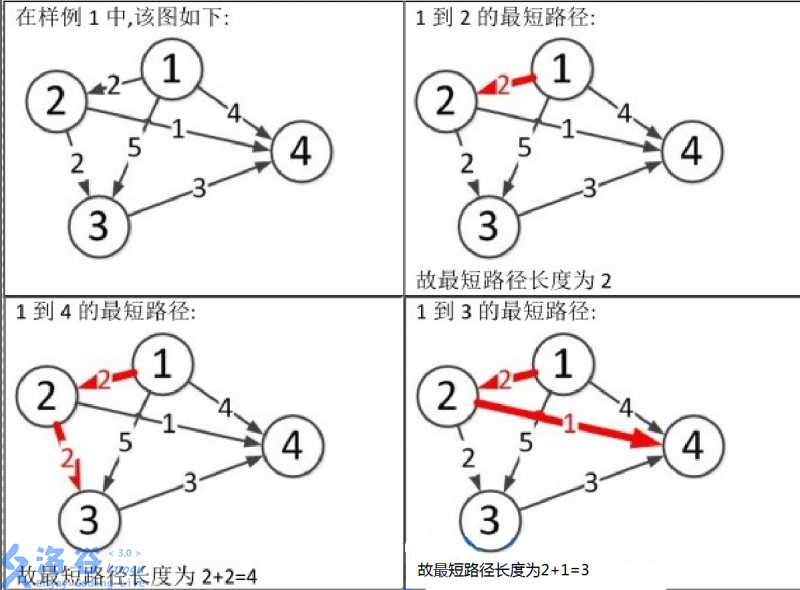
首先，我们先来定义一波变量吧：

struct node{
	int v,w;
	node (){ }
	node (int _v,int _w){
		v=_v;
		w=_w;
	}//构造函数
};

queue<int>qu;//必备队列

const int inf=0x3f3f3f3f;//最大值

vector<node> g[10010];//动态数组存点集
int inq[10010],dst[10010];//标记数组以及确认的最短路经
int n,m;

然后再来一个存图函数

void add(int u,int v,int w){
	g[u].push_back(node(v,w));
}

好了，基本的变量函数已经准备好了，现在就开始我们的SPFA。

但需要传什么参数进去呢？那就简洁点，就只要一个s（松弛的点）

void spfa(){

}

首先我们来给dst赋一个最大值，因为求最短路嘛，当然要赋一个最大值嘛。

memset(dst,inf,sizeof dst);

然后就标记+dst还原成0+放进队列

int u=s;
dst[u]=0;
inq[u]=1;
qu.push(u);

下面就开始一波日常的操作：

while (!qu.empty()){
		u=qu.front();
		qu.pop();//弹出去，不然就出不去了（无限循环）
		inq[u]=0;//取消标记，万一会重复走呢？
		for (int i=0;i<g[u].size();i++){
			int v=g[u][i].v;
			int w=g[u][i].w;//取出来，简洁
			if (dst[v]>dst[u]+w){
				dst[v]=dst[u]+w;//如果松弛了更小，那就松弛吧
				if (!inq[v]){
					qu.push(v);
					inq[v]=1;//如果没走过，那就放进qu在标记一下
				}
			}
		}
	}

main函数里就不用讲了嘛：

int main(){
	int s;
	cin>>n>>m>>s;
	while (m--){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
	}
	spfa(s);
	for (int i=1;i<=n;i++){
		if(dst[i]==0x3f3f3f3f){
			cout<<2147483647<<" ";
		}else{
			cout<<dst[i]<<" ";
		}
	}
	return 0;
}

最后，完整的代码为：

#include <bits/stdc++.h>
using namespace std;
struct node{
	int v,w;
	node (){ }
	node (int _v,int _w){
		v=_v;
		w=_w;
	}
};

queue<int>qu;

const int inf=0x3f3f3f3f;

vector<node> g[10010];
int inq[10010],dst[10010];
int n,m;

void add(int u,int v,int w){
	g[u].push_back(node(v,w));
}

void spfa(int s){
	memset(dst,inf,sizeof dst);
	int u=s;
	dst[u]=0;
	inq[u]=1;
	qu.push(u);
	while (!qu.empty()){
		u=qu.front();
		qu.pop();
		inq[u]=0;
		for (int i=0;i<g[u].size();i++){
			int v=g[u][i].v;
			int w=g[u][i].w;
			if (dst[v]>dst[u]+w){
				dst[v]=dst[u]+w;
				if (!inq[v]){
					qu.push(v);
					inq[v]=1;
				}
			}
		}
	}
}

int main(){
	int s;
	cin>>n>>m>>s;
	while (m--){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
	}
	spfa(s);
	for (int i=1;i<=n;i++){
		if(dst[i]==0x3f3f3f3f){
			cout<<2147483647<<" ";
		}else{
			cout<<dst[i]<<" ";
		}
	}
	return 0;
}

完美结束