HDU1560 DNA sequence —— IDA*算法

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1560

DNA sequence

Time Limit: 15000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2999    Accepted Submission(s): 1462

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein
sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence
of it.

For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

 

Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any
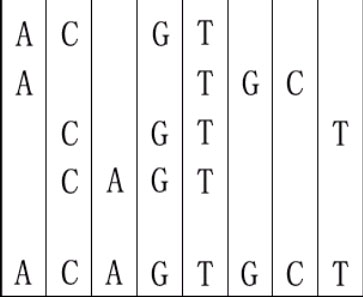
sequence is between 1 and 5.

 

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

 

Sample Input

1
4
ACGT
ATGC
CGTT
CAGT

 

Sample Output

8

 

Author

LL

 

Source

HDU 2006-12 Programming Contest

题解：

一开始以为是直接用回溯的方法，结果TLE。看了题解是用IDA*（迭代加深搜），其实自己不太了解迭代加深搜为什么比较快，而且什么时候用合适？下面是自己对迭代加深搜的一些浅薄的了解：

1.首先迭代加深搜适合用在：求最少步数（带有BFS的特点）并且不太容易估计搜索深度的问题上，同时兼有了BFS求最少步数和DFS易写、无需多开数组的特点。

2.相对于赤裸裸的回溯，迭代加深搜由于限制了搜索深度，所以也能适当地剪枝。

3.我编不下去了……

代码一：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;

 int n;
 char dna[MAXN][MAXN];
 int len[MAXN], pos[MAXN];
 char s[] = {'A', 'G', 'C', 'T'};

 bool dfs(int k, int limit)  //k为放了几个， k+1才为当前要放的
 {
     int maxx = , cnt = ;  //maxx为最长剩余的dna片段， cnt为剩余的片段之和（核苷酸链？好怀念啊）
     for(int i = ; i<n; i++)
     {
         cnt += len[i]-pos[i];
         maxx = max(maxx, len[i]-pos[i]);
     }
     if(cnt==) return true;    //如果片段都放完，则已得到答案
     if(cnt<=limit-k) return true;   //剪枝：片段之和小于等于剩余能放数量，肯定能够得到答案
     if(maxx>limit-k) return false;  //剪枝：最小的估计值都大于剩余能放数量，肯定不能得到答案

     int tmp[MAXN];
     for(int i = ; i<; i++)
     {
         memcpy(tmp, pos, sizeof(tmp));
         bool flag = false;
         for(int j = ; j<n; j++)
             if(dna[j][pos[j]]==s[i])
                 pos[j]++, flag = true;

         //k+1<=limit：在限制范围内
         if(k+<=limit && flag && dfs(k+, limit) )
             return true;
         memcpy(pos, tmp, sizeof(pos));
     }
     return false;
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         int limit = ;
         for(int i = ; i<n; i++)
         {
             scanf("%s",dna[i]);
             len[i] = strlen(dna[i]);
             limit = max(limit, len[i]);
         }

         ms(pos, );
         while(!dfs(, limit))
             limit++;
         printf("%d\n", limit);
     }
 }

代码二：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = +;

 int n;
 char dna[MAXN][MAXN];
 int len[MAXN], pos[MAXN];
 char s[] = {'A', 'G', 'C', 'T'};

 bool dfs(int k, int limit)  //k为放了几个， k+1才为当前要放的
 {
     if(k>limit) return false;

     int maxx = , cnt = ;  //maxx为最长剩余的dna片段， cnt为剩余的片段之和（核苷酸链？好怀念啊）
     for(int i = ; i<n; i++)
     {
         cnt += len[i]-pos[i];
         maxx = max(maxx, len[i]-pos[i]);
     }
     if(cnt==) return true;    //如果片段都放完，则已得到答案
     if(cnt<=limit-k) return true;   //剪枝：片段之和小于等于剩余能放数量，肯定能够得到答案
     if(maxx>limit-k) return false;  //剪枝：最小的估计值都大于剩余能放数量，肯定不能得到答案

     int tmp[MAXN];
     for(int i = ; i<; i++)
     {
         memcpy(tmp, pos, sizeof(tmp));
         bool flag = false;
         for(int j = ; j<n; j++)
             if(dna[j][pos[j]]==s[i])
                 pos[j]++, flag = true;

         if(flag && dfs(k+, limit) )
             return true;
         memcpy(pos, tmp, sizeof(pos));
     }
     return false;
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         int limit = ;
         for(int i = ; i<n; i++)
         {
             scanf("%s",dna[i]);
             len[i] = strlen(dna[i]);
             limit = max(limit, len[i]);
         }

         ms(pos, );
         while(!dfs(, limit))
             limit++;
         printf("%d\n", limit);
     }
 }