[Codeforces 1011E] Border

[题目链接]

https://codeforces.com/contest/1011/problem/E

[算法]

 裴蜀定理 ： 设为n个整数，d是它们的最大公约数，那么存在整数 使得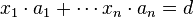 

显然 ， 我们只需求出a1,a2...an模k意义下的最大公约数G，然后枚举G的倍数即可

时间复杂度 ： O(NlogK)

[代码]

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200010

int n , k;
int a[MAXN];

template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
inline int gcd(int x,int y)
{
        if (y == ) return x;
        else return gcd(y,x % y);
}

int main()
{

        read(n); read(k);
        for (int i = ; i <= n; i++)
        {
                read(a[i]);
                a[i] %= k;
                if (a[i] == ) a[i] = k;
        }
        int g = a[];
        for (int i = ; i <= n; i++) g = gcd(g,a[i]);
        set< int > ans;
        int now = ;
        for (int i = ; i < k; i++)
        {
                ans.insert(now);
                now = (now + g) % k;
        }
        printf("%d\n",(int)ans.size());
        for (set< int > :: iterator it = ans.begin(); it != ans.end(); it++) printf("%d ",*it);
        printf("\n");

        return ;

}