Codeforces Round #419 (Div. 1) 补题 CF 815 A-E

A-C传送门

D Karen and Cards

技巧性很强的一道二分优化题

题意很简单 给定n个三元组，和三个维度的上限，问存在多少三元组，使得对于给定的n个三元组中的每一个，必有两个维度严格小于。

首先我们根据一个维度（c维）对n个三元组排序，然后枚举答案在这个维度的取值。

此时序列被分成了两个部分，前半部分 满足所有c大于等于i 后半部分满足所有c严格小于i（即已有一个维度小于）

通过累计，我们知道此时前半部a维的最大值ma和b维的最大值mb.

显然可能存在的三元组答案，必然首先满足a维和b维严格大于ma和mb.

后面我们考虑对于后半部分，即c严格小于i的部分，可能存在某些三元组 ai和bi非常大，以致于上边的答案不合法。

这时，我们想知道，对于ai大于ma的那些三元组，其对应的bi能有多大？

我们可以用一个mx数组提前统计这个值。

那么，当ai大到一定程度，其对应的bi就不可能大于mb了 我们可以二分找到这个边界ret

对于ma到ret这个范围的值，我们让第一维取其中的某个值，对应的第二维b有多少种可能呢？

所有ai大于当前值的对应的bi的最大值。 因为若ai小于当前值，就不需要保证第二维大于bi了。。

具体看代码吧 有点难以描述。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define maxn 500005
#define ll long long
using namespace std;

ll sum[maxn],mx[maxn];

ll n,p,q,r;

ll ans;

struct note{
	int a,b,c;
}a[maxn];

bool cmp(note i,note j){
	return i.c>j.c;
}

int main(){
	scanf("%I64d%I64d%I64d%I64d",&n,&p,&q,&r);
	fo(i,1,n) scanf("%d%d%d",&a[i].a,&a[i].b,&a[i].c);
	fo(i,1,n) mx[a[i].a]=max(mx[a[i].a],(ll)a[i].b+1);
	fd(i,p,1) mx[i]=max(mx[i+1],mx[i]);//可能存在的最大b值
	fo(i,1,p) sum[i]=sum[i-1]+(q-mx[i])+1;
	ll ma=1,mb=1;
	sort(a+1,a+n+1,cmp);
	int wz=1;
	fd(i,r,1) {
		while (wz<=n && a[wz].c==i) {
			ma=max(ma,a[wz].a+1ll);
			mb=max(mb,a[wz].b+1ll);
			wz++;
		}
		if (ma>p || mb>q) break;
		int x=ma,y=p,ret=ma-1;
		while (x<=y) {
			int mid=(x+y) >> 1;
			if (mx[mid]>=mb) {
				x=mid+1;
				ret=mid;
			}
			else y=mid-1;
		}
		ans+=sum[ret]-sum[ma-1]+1ll*(p-ret)*(q-mb+1);
	}
	cout<<ans;
	return 0;
}

E Karen and Neighborhood

题意非常简单 不必赘述

整个过程其实是一个满二叉树的层次遍历，问我们遍历到的第k个元素是哪一个。对数复杂度

先给出遍历的二叉树 其规律非常明显

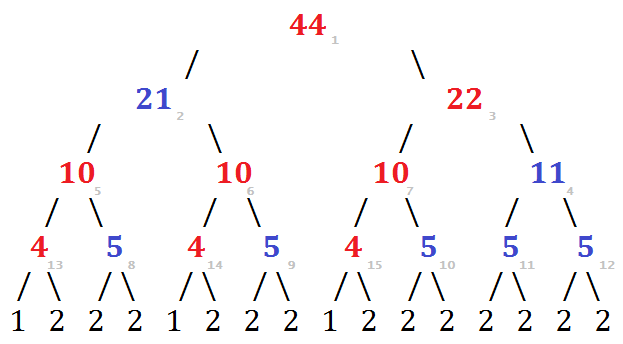
我们可以在对数时间内快速寻找到第k个节点，但是我们的空间不足以储存所有的节点信息。

那么怎么办呢？ 我们首先判断这个节点在哪一个层次，即它与邻居的最短距离是多少。

然后我们再二分判断这个节点在整个序列中的位置，我们可以快速判断一个区间产生能够产生多少个距离为len的子节点。与k比较即可。

于是总的复杂度是二分套二分 即O（lognlogn）

这道题让我们深入理解了满二叉树的层次遍历

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k;
int main(){
	scanf("%lld%lld",&n,&k);
	if(k==1)return printf("1"),0;
	if(k==2)return printf("%lld",n),0;
	n-=2,k-=3;
	map<ll,ll>f,g,nxt;
	g[n]=1;
	while(g.size()){
		nxt.clear();
		for(auto s:g)if(s.first)
			f[-((s.first-1)>>1)]+=s.second,
			nxt[(s.first)>>1]+=s.second,
			nxt[(s.first-1)>>1]+=s.second;
		g=nxt;
	}
	for(auto s:f){
		//printf("[%d]",s.first);
		if(s.second>k){//确定在哪一层
			ll l=1,r=n,len=-s.first;
//			printf("[%d]",len);
			while(true){
				if(((r-l)>>1)==len&&k==0)
					return printf("%lld",((r-l)>>1)+1+l),0;
				map<ll,ll>A,B,C;
				ll mid=l+r>>1;
				A[mid-l]=1;
				B[(r-l)>>1]=1;
				while(A.size()){
					C.clear();
					for(auto qs:A)if(qs.first)
						B[(qs.first-1)>>1]+=qs.second,//
						C[(qs.first)>>1]+=qs.second,
						C[(qs.first-1)>>1]+=qs.second;
					A=C;
				}
			//	printf("[%d]",B[len]);
				if(B[len]>k)r=mid-1;
				else l=mid+1,k-=B[len];
			}
		} else k-=s.second;
	}
}