10.22~10.28一周经典题目整理（meeting，BZOJ4377，POJ3659）

meeting：给正n边形每个点染上黑色或者白色，问有多少个同色的等腰三角形。

　　以正五边形为例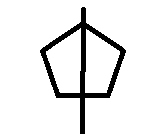这里将最上面的点作为顶点，得到若干对相等的腰

，注意到以最上面的点作为顶点的等腰三角形的个数，等于颜色相等且都为顶点颜色的对称点的个数。

O(n^2)统计即可。

PS：注意减去等边三角形的情况。

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <cstdlib>
 #include <ctime>
 #include <cmath>
 #include <algorithm>
 #include <set>
 #include <map>
 #include <queue>

 #define N 1000010
 #define LL long long

 using namespace std;

 int n, cnt0[], cnt1[];
 char S[N];

 int pos(int i){    //i做镜像操作后的位置
     if(i==) return i;
     return n-i;
 }

 LL calc0(){
     if(n <= ) return ;
     LL ans = ;
     for(int s=;s<n;s++) {
         int tmp = ;
         for(int i=, j=s;i<n;i++) {
             if(S[i] == S[s] && S[pos(j)] == S[s]) {
                 if(i != s && pos(j) != i && pos(j) != s) ans ++;
                 else if((i == s || pos(j) == s) && pos(j) != i) tmp ++;
             }
             cout << i << " match " << j << endl;
             j = (j-+n)%n;
         }
         cout << endl;
     //    cout << n << " tmp = " << tmp << endl;
     }
     ans/=;
     return ans;
 }

 LL calc_ex(){
     if((n-) %  != ) return 0LL;
     int ans = ;
     int t = n/;
     for(int i=;i<n;i++)
         if(S[i] == S[(i+t)%n] && S[i] == S[(i+*t)%n]) ans ++;
     return (ans/3LL) * 2LL;
 }

 int main() {
     freopen("test.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--) {
         scanf("%s",S);
         n=strlen(S);
         //cout << calc0() << endl;
         cout << calc0()-calc_ex() << endl;
     }
     return ;
 }

POJ3659：新颖的题目，有一个长度为n的整数序列，数字两两不同，给出m个Li到Ri最小值为vi的命题，问到第几个最先出现冲突。

首先，二分是必然的，接下来就考虑如何判定二分出的若干个命题是否冲突。

Li到Ri最小值为vi 等价于 对于j∈[Li,Ri] 有aj >= vi，且必然存在aj = vi。

从而将命题按vi从大到小排序，并对于所有vi相同的区间算出 [L交,R交]，冲突一定出在

　　1.前面的命题和后面的命题冲突（前面的命题限制了所有的aj ∈[L交,R交]，有aj>vi）

　　2.vi相同的命题冲突（vi相同的区间的交为空）

线段树/并查集即可。

PS：在考虑当前vi相等的区间们 对后面区间们的影响时要考虑并集。

 #include <cstdio>
 #include <algorithm>
 #include <iostream>

 #define l(x) ch[x][0]
 #define r(x) ch[x][1]
 #define LL long long

 const int N = ;

 using namespace std;

 struct node{
     int l,r,v;
 }a[N],b[N];

 int totn,n,m,a0[N<<];
 int ch[N<<][],setv[N<<],minv[N<<];

 int build(int l,int r){
     int x=++totn;
     minv[x]=setv[x]=;
     if(l==r) return x;
     int mid=(l+r)>>;
     l(x)=build(l,mid);
     r(x)=build(mid+,r);
     return x;
 }

 void update(int x){
     minv[x] = min(minv[l(x)],minv[r(x)]);
 }

 void push(int x,int l,int r){
     if(!setv[x]) return;
     setv[l(x)] = max(setv[l(x)],setv[x]);
     setv[r(x)] = max(setv[r(x)],setv[x]);
     minv[l(x)] = max(minv[l(x)],setv[x]);
     minv[r(x)] = max(minv[r(x)],setv[x]);
     setv[x]=;
 }

 int qmin(int x,int l,int r,int ql,int qr){
     push(x,l,r);
     if(ql<=l && r<=qr) return minv[x];
     int mid=(l+r)>>,ans=0x3f3f3f3f;
     if(ql<=mid) ans = min(ans,qmin(l(x),l,mid,ql,qr));
     if(mid<qr)  ans = min(ans,qmin(r(x),mid+,r,ql,qr));
     update(x);
     return ans;
 }

 void change(int x,int l,int r,int ql,int qr,int qv){
     push(x,l,r);
     if(ql<=l && r<=qr){
         setv[x]=qv;
         minv[x]=max(minv[x],qv);
         return;
     }
     int mid=(l+r)>>;
     if(ql<=mid) change(l(x),l,mid,ql,qr,qv);
     if(mid<qr)  change(r(x),mid+,r,ql,qr,qv);
     update(x);
 }

 bool cmp(node a, node b){
     return a.v>b.v;
 }

 bool check(int t){
     int tot=;
     for(int i=;i<=t;i++) b[++tot]=a[i];
     totn=;
     build(,a0[]);
     sort(b+,b+tot+,cmp);
     int j=;
     while(j<=tot){
         int l=b[j].l,r=b[j].r,L=b[j].l,R=b[j].r;
         while(j<tot && b[j+].v==b[j].v){
             l =max(l,b[j+].l);
             r =min(r,b[j+].r);
             L =min(L,b[j+].l);
             R =max(R,b[j+].r);
             j++;
         }
         if(l>r) return ;
         int tp = qmin(,,a0[],l,r);
         if(tp>b[j].v) return ;
         change(,,a0[],L,R,b[j].v);
         j++;
     }
     return ;
 }

 int a1[N];

 void prework(){
     for(int i=;i<=m;i++) a1[i]=a[i].v;
     sort(a1+,a1+m+);
     int tot1=;
     for(int i=;i<=m;i++) if(a1[i]!=a1[i-]) a1[++tot1]=a1[i];
     for(int i=;i<=m;i++) a[i].v = lower_bound(a1+,a1+tot1+,a[i].v)-a1;
 }

 int main(){
 //    freopen("test.txt","r",stdin);
 //    freopen("mine.out","w",stdout);
 //    puts("error");
     scanf("%d%d",&n,&m);
 //    cout<<n<<' '<<m<<endl;
         a0[]=;
         for(int i=;i<=m;i++) {
             scanf("%d%d%d",&a[i].l,&a[i].r,&a[i].v);
             a0[++a0[]]=a[i].l;
             a0[++a0[]]=a[i].r;
         }
         prework();
         sort(a0+,a0+a0[]+);
         int tot0=;
         for(int i=;i<=a0[];i++) if(a0[i]!=a0[i-]) a0[++tot0]=a0[i];
         a0[]=tot0;
         for(int i=;i<=tot0;i++) if(a0[i]!=a0[i-]+) a0[++a0[]]=a0[i-]+;
         sort(a0+,a0+a0[]+);
         for(int i=;i<=m;i++){
             a[i].l=lower_bound(a0+,a0+a0[]+,a[i].l)-a0;
             a[i].r=lower_bound(a0+,a0+a0[]+,a[i].r)-a0;
         }
         int l=,r=m;
         while(r-l>){
             int mid=(l+r)>>;
             if(!check(mid)) r=mid;
             else l=mid;
         }
         for(int i=l;i<=r;i++)
             if(!check(i)){
                 printf("%d\n",i);
                 return ;
             }
         puts("");
     return ;
 }
 /*
 20 4
 1 10 7
 5 19 7
 3 12 8
 11 15 12
 */

BZOJ4377：题目有些累赘，见官网。

注意到c[i]%n得到0~n-1 。且一一对应。

所以考虑有多少个自序序列等于给定串，相当于考虑有多少个i满足从i开始的m个字符能和给定串匹配。

排除最后的m-1个i，本题相当于问有多少个x，满足

　　(x + i*a) %n < P    (c[i] == 0)

　　(x + i*a) %n >= P  (c[i] == 1)

对于这m个等式，每一个等式可以得到一个不满足条件的x的取值区域。

对这2*m个区间求并取反集就是答案区间。

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <cstdlib>
 #include <ctime>
 #include <cmath>
 #include <algorithm>
 #include <set>
 #include <map>
 #include <queue>

 #define LL long long
 #define N 1000010

 using namespace std;

 LL n,a,b,P;
 int m,tot;
 char c[N];

 struct node{
     int l,r;
 }q[*N];

 bool cmp(node a,node b){
     return a.l<b.l;
 }

 int main(){
     freopen("test.txt","r",stdin);
     cin>>n>>a>>b>>P>>m;
     while(!isdigit(c[]=getchar()));
     for(int i=;i<m;i++) c[i]=getchar();
     int ans=n;
     LL tmp;
     tmp=b%n;
     for(int i=;i<m;i++){
         tmp=(tmp-a+n) % n;
         q[++tot] = (node){(int)tmp,(int)tmp};
     }
     for(int i=;i<m;i++){
         LL l,r;
         if(c[i]=='') l=-i*a,r=P-1LL-i*a;
         else l=P-i*a,r=n-1LL-i*a;
         l=(l%n+n)%n;
         r=(r%n+n)%n;
         if(l>r){
             q[++tot]=(node){,(int)r};
             q[++tot]=(node){(int)l,(int)(n-)};
         }
         else q[++tot] = (node){(int)l,(int)r};
     }
 //    for(int i=1;i<=tot;i++) cout<<q[i].l<<' '<<q[i].r<<endl;
     sort(q+,q+tot+,cmp);
     LL l=q[].l,r=q[].r;
     for(int i=;i<=tot;i++){
         if(q[i].l>r){
             ans-=(int)(r-l+);
             l=q[i].l;
             r=q[i].r;
         }
         else r=max(r,(LL)q[i].r);
     }
     ans-=(int)(r-l+);
     printf("%d\n",ans);
     return ;
 }

hdu5299（待补完博弈论理论），平面上有n个圆，圆与圆互不相切相交，Alice，Bob轮流选圆，每一次删掉选定圆与其包含的所有圆，问是否先手必胜。

每个圆和第一个包含它的圆连边，得到一个森林。

本题博弈论部分是经典模型，关键在于如何建出树来。

首先对于所有的圆，它们的上下关系不会发生变化，所以考虑用set来维护。

将xi-Ri和xi+Ri作为扫描线，x从小到大枚举。

圆在set中的权值 为  圆与当前x的靠上交点的y坐标，这样对于每一个加进来的圆，lowerbound一下就好了。

注意lowerbound到的第一个圆不一定是加进来的圆的father（可能同为子节点），如果不是要一直沿着树向上找，直到找到其father。

这个过程可以二分一下（因为越向上包含当前圆的可能性越大），向上找的过程用倍增就好了。

PS：我懒，写的暴力上翻。

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <cstdlib>
 #include <ctime>
 #include <cmath>
 #include <algorithm>
 #include <set>
 #include <map>
 #include <queue>

 #define eps 1e-8
 #define LD double
 #define sqr(x) ((x)*(x))
 #define N 40010
 #define LL long long

 using namespace std;

 int X;

 struct edge{
     int x,to;
 }E[N];

 struct node{
     int x,y,R;
     int id;
     void scan(){
         scanf("%d%d%d",&x,&y,&R);
     }
     bool operator<(const node &a)const{
         LD t0 = sqrt(sqr(R)-(LD)sqr((LD)X-(LD)x)) + (LD)y;
         LD t1 = sqrt(sqr(a.R)-(LD)sqr((LD)X-(LD)a.x)) + (LD)a.y;
         if(fabs(t0-t1)<eps) return ;
         return t0<t1;
     }
 }a[N],b[N],a0[N];

 set<node> Tp; 

 int n;
 int X0[N<<];

 bool cmp1(node a,node b){
     return a.x-a.R<b.x-b.R;
 }

 bool cmp2(node a,node b){
     return a.x+a.R<b.x+b.R;
 }

 int totE,g[N],sg[N],fa[N];
 bool vis[N];

 void ade(int x,int y){
 //    cout<<"ade "<<x<<' '<<y<<endl;
     E[++totE]=(edge){y,g[x]}; g[x]=totE;
     fa[y]=x;
 }

 #define p E[i].x

 int dfs(int x){
 //    bool flag=0;
 //    for(int i=g[x];i;i=E[i].to) dfs(p),flag=1;
 //    if(!flag) return sg[x]=0;
 //    for(int i=g[x];i;i=E[i].to) vis[sg[p]]=1;
 //    for(sg[x]=0;vis[sg[x]];sg[x]++);
 //    for(int i=g[x];i;i=E[i].to) vis[sg[p]]=0;
 //    return sg[x];
     int ans=;
     for(int i=g[x];i;i=E[i].to) ans^=dfs(p)+;
     return ans;
 }

 int main(){
     freopen("test.txt","r",stdin);
     //freopen(".out","w",stdout);
     int T;
     scanf("%d",&T);
     while(T--){
         memset(g,,sizeof(g));
         memset(fa,,sizeof(fa));
         totE=;
         scanf("%d",&n);
         for(int i=;i<=n;i++){
             a[i].scan();
             a[i].id=i; b[i]=a[i];
             a0[i]=a[i];
         }
         X0[]=;
         for(int i=;i<=n;i++){
             X0[++X0[]]=a[i].x-a[i].R;
             X0[++X0[]]=a[i].x+a[i].R;
         }
         sort(X0+,X0+X0[]+);
         int tot=;
         for(int i=;i<=X0[];i++)
             if(X0[i]!=X0[i-]) X0[++tot]=X0[i];
         sort(a+,a+n+,cmp1);
         sort(b+,b+n+,cmp2);
         set<node>::iterator it;
         Tp.clear();
         int j=,k=;
         for(int i=;i<=tot;i++){
             X=X0[i];
             while(k<=n && b[k].x+b[k].R==X0[i]){
                 it=Tp.find(b[k]);
                 Tp.erase(it);
                 k++;
             }
             while(j<=n && a[j].x-a[j].R==X0[i]){
                 it=Tp.lower_bound(a[j]);
                 if(it!=Tp.end()){
                     int t=it->id;
                     while(t){
                         if(sqr(a0[t].x-(LL)a[j].x)+sqr(a0[t].y-(LL)a[j].y)<sqr((LL)a0[t].R)){
                             ade(t,a[j].id);
                             break;
                         }
                         t=fa[t];
                     }
                 }
                 Tp.insert(a[j]);
                 j++;
             }
         }
         int ans=;
         for(int i=;i<=n;i++) if(!fa[i]) ans^=dfs(i)+;
         if(ans) puts("Alice");
         else puts("Bob");
     }
     return ;
 }

hdu5290：一棵树，边权为1，每个点有一个≤100的爆炸半径Ri，如果引爆i点，到i点距离小于等于Ri的点都会被炸掉，问最少引爆多少点，

注意到影响状态的无非要炸的深度和点。

f[i][j]表示爆炸还需要从i点向下传播j层 最少炸的次数（注意j可能为负）

dp即可，O(nm)