最小生成树 Prim算法 Kruskal算法实现

最小生成树定义

最小生成树是一副连通加权无向图中一棵权值最小的生成树。

在一给定的无向图 G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即，而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即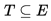）且为无循环图，使得的 w(T) 最小，则此 T 为 G 的最小生成树。

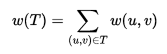
最小生成树其实是最小权重生成树的简称。

一个连通图可能有多个生成树。当图中的边具有权值时，总会有一个生成树的边的权值之和小于或者等于其它生成树的边的权值之和。广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树。

——以上内容摘自中文维基百科

通俗一点讲就是 通过可行边遍历所有点，使这些边权值相加最小（可能吧）

Prim算法

类似于dijistra算法 需要用到蓝白点的思想 ……不会dijistra也没关系 不智障就够了

从单一顶点开始，普里姆算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。

输入：一个加权连通图，其中顶点集合为V，边集合为E；

初始化：V_new = {x}，其中x为集合V中的任一节点（起始点），E_new；

重复下列操作，直到V_new = V：

{

在集合E中选取权值最小的边（u, v），其中u为集合V_new中的元素，而v则是V中没有加入V_new的顶点（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

将v加入集合V_new中，将（u, v）加入集合E_new中；

}

输出：使用集合V_new和E_new来描述所得到的最小生成树。

图例	说明	不可选	可选	已选
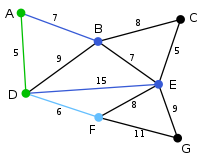
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
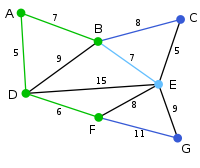
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
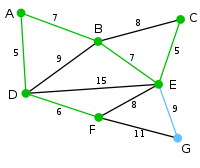
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

Kruskal算法

基本思想：

（1）构造一个只含n个顶点，边集为空的子图。若将图中各个顶点看成一棵树的根节点，则它是一个含有n棵树的森林。

（2）从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图。也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之

（3）依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

通俗地讲 就是：将图中的所有边都去掉，然后将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环，重复上一步直到连接所有顶点，此时就生成了最小生成树blahblahblah……

步骤：

1.新建图G，G中拥有原图中相同的节点，但没有边

2.将原图中所有的边按权值从小到大排序

3.从权值最小的边开始，如果这条边连接的两个节点于图G中不在同一个连通分量中，则添加这条边到图G中（并查集的思想）

4.重复3，直至图G中所有的节点都在同一个连通分量中(即所有点都加入最小生成树了)

那么怎么判断两个节点是否在一个强连通分量中呢？

建议先学完并查集（http://www.cnblogs.com/cyjb/p/UnionFindSets.html）

解决办法：使用并查集，分别找出两个顶点u, v所在树的根节点。若根节点（祖先）相同，说明u, v在同一棵树中（在同一个集合中），则u, v连接起来会形成环；若根节点不同，则u, v不在一棵树中，连接起来不会形成环，而是将两棵树合并。

代码就不贴了

总结

无疑，Kruskal算法在效率上要比Prim算法快，因为Kruskal只需要对权重边做一次排序，而Prim算法则需要做多次排序。尽管Prim算法每次做的算法涉及的权重边不一定会涵盖连通图中的所有边，但是随着所使用的排序算法的效率的提高，Kruskal算法和Prim算法之前的差异将会清晰的显性出来。

若有瑕疵 请谅解并纠正 感激不尽