求n的因子个数与其因子数之和

方法一：朴素算法：O(n)。

 #include<bits/stdc++.h>
 using namespace std;
 int get_num(int n){
     int num=;
     for(int i=;i<=n;++i)
         if(n%i==)num++;
     return num;
 }
 int get_sum(int n){
     int tot=;
     for(int i=;i<=n;++i)
         if(n%i==)tot+=i;
     return tot;
 }
 int main(){
     int n;
     while(cin>>n){
         cout<<get_num(n)<<endl;//求n的因子个数
         cout<<get_sum(n)<<endl;//求n的因子数之和
     }
     return ;
 }

方法二：约数个数定理：O(√n)。

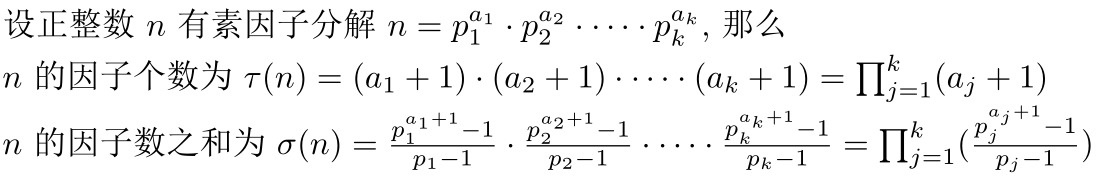
 #include<bits/stdc++.h>
 using namespace std;
 int get_num(int n){
     int tot=;
     for(int i=;i*i<=n;++i){
         if(n%i==){
             int x=;
             while(n%i==){
                 n/=i;
                 x++;
             }
             tot*=(x+);
         }
     }
     if(n>)tot*=;
     return tot;
 }
 int get_sum(int n){
     int tot=;
     for(int i=;i*i<=n;i++){
         if(n%i==){
             int mul=;
             while(n%i==){
                 n/=i;
                 mul*=i;
             }
             tot*=(mul*i-)/(i-);
         }
     }
     if(n>)tot*=(n+);
     return tot;
 }
 int main(){
     int n;
     while(cin>>n){
         cout<<get_num(n)<<endl;//求n的因子个数
         cout<<get_sum(n)<<endl;//求n的因子数之和
     }
     return ;
 }

实战例题：

题解报告：hdu 2521 反素数

Problem Description

反素数就是满足对于任意i(0<i<x),都有g(i)<g(x),(g(x)是x的因子个数),则x为一个反素数。现在给你一个整数区间[a,b],请你求出该区间的x使g(x)最大。

Input

第一行输入n,接下来n行测试数据
输入包括a,b, 1<=a<=b<=5000,表示闭区间[a,b].

Output

输出为一个整数,为该区间因子最多的数.如果满足条件有多个,则输出其中最小的数.

Sample Input

3
2 3
1 10
47 359

Sample Output

2 6 240

Hint

2的因子为：1 2

10的因子为:1 2 5 10

解题思路：求区间[a,b]中最小的元素x，使得所含的因子个数最大，由于数据比较小，暴力枚举区间[a,b]并套一下公式即可。时间复杂度为O($n\sqrt{n}$)。

AC代码(15ms)：

 #include<bits/stdc++.h>
 using namespace std;
 int n,a,b,maxnum,maxindex;
 int get_num(int n){//求n的因子个数
     int tot=;
     for(int i=;i*i<=n;++i){
         if(n%i==){
             int x=;
             while(n%i==){
                 n/=i;
                 x++;
             }
             tot*=(x+);
         }
     }
     if(n>)tot*=;
     return tot;
 }
 int main(){
     while(cin>>n){
         while(n--){
             cin>>a>>b;maxnum=;maxindex=a;
             for(int i=a;i<=b;++i){
                 int tmp=get_num(i);
                 if(tmp>maxnum){maxindex=i;maxnum=tmp;}
             }
             cout<<maxindex<<endl;
         }
     }
     return ;
 }

题解报告：hdu 1215 七夕节

Problem Description

七夕节那天,月老来到数字王国,他在城门上贴了一张告示,并且和数字王国的人们说:"你们想知道你们的另一半是谁吗?那就按照告示上的方法去找吧!"
人们纷纷来到告示前,都想知道谁才是自己的另一半.告示如下:

数字N的因子就是所有比N小又能被N整除的所有正整数,如12的因子有1,2,3,4,6.
你想知道你的另一半吗?

Input

输入数据的第一行是一个数字T(1<=T<=500000),它表明测试数据的组数.然后是T组测试数据,每组测试数据只有一个数字N(1<=N<=500000).

Output

对于每组测试数据,请输出一个代表输入数据N的另一半的编号.

Sample Input

Sample Output

解题思路：求n的因子数之和，简单套一下公式，时间复杂度为O($t\sqrt{n}$)，最坏大概为3e8。

AC代码一(93ms)：

 #include<bits/stdc++.h>
 using namespace std;
 int t,n;
 int get_sum(int n){
     int tot=;
     for(int i=;i*i<=n;++i){
         if(n%i==){
             int mul=;
             while(n%i==){
                 n/=i;
                 mul*=i;
             }
             tot*=(mul*i-)/(i-);
         }
     }
     if(n>)tot*=(n+);
     return tot;
 }
 int main(){
     while(~scanf("%d",&t)){
         while(t--){
             scanf("%d",&n);
             printf("%d\n",get_sum(n)-n);
         }
     }
     return ;
 }

AC代码二(109ms)：简单打表，时间复杂度为nlogn。

 #include<bits/stdc++.h>
 const int maxn=;
 using namespace std;
 int t,n,sum[maxn];
 int main(){
     for(int i=;i<maxn/;++i)//因子i
         for(int j=i*;j<maxn;j+=i)//j是i的倍数，即j的因子是i
             sum[j]+=i;//sum[j]表示其所有因子之和
     while(~scanf("%d",&t)){
         while(t--){
             scanf("%d",&n);
             printf("%d\n",sum[n]);
         }
     }
     return ;
 }

题解报告：hdu 1999 不可摸数

Problem Description

s(n)是正整数n的真因子之和，即小于n且整除n的因子和.例如s(12)=1+2+3+4+6=16.如果任何数m，s(m)都不等于n,则称n为不可摸数.

Input

包含多组数据，首先输入T,表示有T组数据.每组数据1行给出n(2<=n<=1000)是整数。

Output

如果n是不可摸数，输出yes，否则输出no

Sample Input

Sample Output

yes

解题思路：题意就是给一个n(n表示为s(m)的真因子数之和)，如果任意数m的真因子之和在n∈[2,1000]，那么s(m)就不是不可摸数，否则为不可摸数。打表可以发现数m只需枚举到10^6便可将真因数之和为1000以内的全部找出来。于是这道题也可以直接打印出89个不可摸数，简单标记一下即可。

AC代码一(62ms)：

 #include<bits/stdc++.h>
 const int maxn=;
 using namespace std;
 int t,n,sum[maxn];bool f[maxn];
 int main(){
     memset(f,false,sizeof(f));
     for(int i=;i<maxn/;++i)//因子i
         for(int j=i*;j<maxn;j+=i)//j是i的倍数，即j的因子是i
             sum[j]+=i;//sum[j]表示其所有因子之和
     for(int i=;i<maxn;++i)
         if(sum[i]<=)f[sum[i]]=true;//如果真因数之和在1000以内，那么sum[i]不是不可摸数
     while(~scanf("%d",&t)){
         while(t--){
             scanf("%d",&n);
             if(f[n])printf("no\n");
             else printf("yes\n");//n为不可摸数
         }
     }
     return ;
 }

AC代码二(0ms)：

 #include<bits/stdc++.h>
 using namespace std;
 int t,n;bool f[];
 int main(){
     int obj[]={,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,,,,,,,
     ,,,,,,};
     memset(f,false,sizeof(f));
     for(int i=;i<;++i)f[obj[i]]=true;//1000以内共有89个数为不可摸数
     while(~scanf("%d",&t)){
         while(t--){
             scanf("%d",&n);
             if(f[n])printf("yes\n");
             else printf("no\n");
         }
     }
     return ;
 }

题解报告：hdu 1299 Diophantus of Alexandria

Problem Description

Diophantus of Alexandria was an egypt mathematician living in Alexandria. He was one of the first mathematicians to study equations where variables were restricted to integral values. In honor of him, these equations are commonly called diophantine equations. One of the most famous diophantine equation is x^n + y^n = z^n. Fermat suggested that for n > 2, there are no solutions with positive integral values for x, y and z. A proof of this theorem (called Fermat's last theorem) was found only recently by Andrew Wiles.
Consider the following diophantine equation:
1 / x + 1 / y = 1 / n where x, y, n ∈ N+ (1)Diophantus is interested in the following question: for a given n, how many distinct solutions (i. e., solutions satisfying x ≤ y) does equation (1) have? For example, for n = 4, there are exactly three distinct solutions:
1 / 5 + 1 / 20 = 1 / 4
1 / 6 + 1 / 12 = 1 / 4
1 / 8 + 1 / 8 = 1 / 4Clearly, enumerating these solutions can become tedious for bigger values of n. Can you help Diophantus compute the number of distinct solutions for big values of n quickly?

Input

The first line contains the number of scenarios. Each scenario consists of one line containing a single number n (1 ≤ n ≤ 10^9).

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Next, print a single line with the number of distinct solutions of equation (1) for the given value of n. Terminate each scenario with a blank line.

Sample Input

1260

Sample Output

Scenario #1:
3

Scenario #2:
113

解题思路：首先，根据分式等式的性质可得x、y均大于n，假设y=n+k(k≥1)，将其代入1/x+1/y=1/n化简得x=n^2/k+n，因为x∈N⁺，所以k|n²(k≥1)，即求n²的因子个数sum，则最终的答案为：(sum+1)/2，因为必定有一半的x、y这一对是重复了的，只是值互换了而已，举个例子：当n=4时，

x= 8 6 5

k= 1 2 4 8 16（n^2=16的所有因子）

y= 6 8

显然此时有3组解，也就是满足n²/k == k，(其中k|n²)的解有(sum+1)/2组。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;int t;LL n;
 LL get_num(LL x){
     LL ans=,tp;
     for(LL i=;i*i<=x;++i){
         if(x%i==){
             tp=;
             while(x%i==)tp++,x/=i;
             ans*=(+*tp);
         }
     }
     if(x>)ans*=;
     return ans;
 }
 int main(){
     while(cin>>t){
         for(int i=;i<=t;++i){
             cin>>n;
             cout<<"Scenario #"<<i<<":\n"<<(get_num(n)+)/<<"\n"<<endl;
         }
     }
     return ;
 }

题解报告：NYOJ #66 分数拆分

描述

现在输入一个正整数k,找到所有的正整数x>=y,使得1/k=1/x+1/y.

输入

第一行输入一个整数n,代表有n组测试数据。
接下来n行每行输入一个正整数k

输出

按顺序输出对应每行的k找到所有满足条件1/k=1/x+1/y的组合。

样例输入

2
2
12

样例输出

1/2=1/6+1/3
1/2=1/4+1/4
1/12=1/156+1/13
1/12=1/84+1/14
1/12=1/60+1/15
1/12=1/48+1/16
1/12=1/36+1/18
1/12=1/30+1/20
1/12=1/28+1/21
1/12=1/24+1/24

解题思路：由x>=y且x、y均大于k可知1/x<=1/y，1/k-1/y<=1/y，即k<y<=2k，所以只需控制y的枚举范围即可。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 int t,k;
 int main(){
     while(cin>>t){
         while(t--){
             cin>>k;
             for(int i=k+;i<=*k;++i)//枚举k+1~2k
                 if(i*k%(i-k)==)printf("1/%d=1/%d+1/%d\n",k,i*k/(i-k),i);//通分，其中(i-k)|(i*k)。
         }
     }
     return ;
 }

财大情侣

Time Limit: 2000/1000ms (Java/Others)

Problem Description:

高考完终于来到梦寐以求的财经大学，男三女七有木有!食堂吃饭前后左右三排都是女生有木有!该学校总共有n个人，每个人都有对应自己的魅力值，从1到n。现规定每个人的情商为每个人魅力值的约数（不包括本身）之和。在广财有个很神奇的事情，当一个人的情商刚好等于另一个的魅力值的时候，这两个人就meant to be情侣（不是一男一女怎么办？随便吧）。
如：220：1+2+4+5+10+11+20+22+44+55+110=284
  　284：1+2+4+71+142=220
这样魅力值为220和284的就成为一对啦。
给定两个数，a，b，找出所有a和b之间(inclusive)成对的。

Input:

输入包含多组测试数据，每组数据输入两个数a,b (0<=a,b<=100000).

Output:

对于每组测试，输出a和b之间的所有情侣。每对情侣占一行，魅力值小的在前面。对于多对情侣，按情侣中魅力值小的排序。参考sample output。

Sample Input:

200 1300
1 200

Sample Output:

220 284
1184 1210
NO
解题思路：求每个数的所有真因子之和，简单打个表再判断一下即可。
AC代码：

 #include<bits/stdc++.h>
 const int maxn=;//范围大一点，否则会出现越界的情况
 using namespace std;
 int a,b,x,sum[maxn];bool flag;
 int main(){
     for(int i=;i<maxn/;++i)//求因子数之和
         for(int j=i*;j<maxn;j+=i)//j初始为i的2倍，以后以i的步长增长，累加j的真因子
             sum[j]+=i;
     while(cin>>a>>b){
         if(a>b)swap(a,b);flag=false;
         for(int i=a;i<=b;++i)//先判断是不是一对情侣，并且前面的因子数之和x要在区间范围内，且前一个数i要小于后一个数x
            if(i==sum[x=sum[i]]&&x<=b&&i<x){flag=true;cout<<i<<' '<<x<<endl;}
         if(!flag)cout<<"NO"<<endl;
     }
     return ;
 }