SPOJ 962 Intergalactic Map (网络最大流)

http://www.spoj.com/problems/IM/

962. Intergalactic Map

Problem code: IM

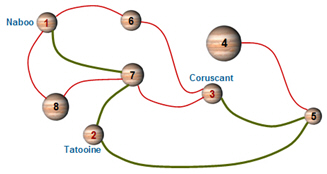Jedi knights, Qui-Gon Jinn and his young apprentice Obi-Wan Kenobi, are entrusted by Queen Padmé Amidala to save Naboofrom an invasion by
the Trade Federation. They must leave Naboo immediately and go to Tatooine to pick up the proof of the Federation’s evil design. They then must proceed on to the Republic’s capital planet Coruscant to produce it in front of
the Republic’s Senate. To help them in this endeavor, the queen’s captain provides them with an intergalactic map. This map shows connections between planets not yet blockaded by the Trade Federation. Any pair of planets has at most one connection between
them, and all the connections are two-way. To avoid detection by enemy spies, the knights must embark on this adventure without visiting any planet more than once. Can you help them by determining if such a path exists? 



Note - In the attached map, the desired path is shown in bold.

Input Description

The first line of the input is a positive integer t ≤ 20, which is the number of test cases. The descriptions of the test cases follow one after the other. The first line of each test case is a pair of positive integers n, m (separated by a single space). 2
≤ n ≤ 30011 is the number of planets and m ≤ 50011 is the number of connections between planets. The planets are indexed with integers from 1 to n. The indices of Naboo, Tatooine and Coruscant are 1, 2, 3 respectively. The next m lines contain two integers
each, giving pairs of planets that have a connection between them.

Output Description

The output should contain t lines. The i^th line corresponds to the i^th test case. The output for each test case should be YES if the required path exists and NO otherwise.

Example

Input

2

3 3

1 2

2 3

1 3

3 1

1 3



Output

YES

NO

题意：

给出一张无向图，要求从1先走到2。再从2走到3，且每一个点至多经过一次，问是否可能。

分析：

每一个点至多经过一次，显然往网络流上靠，很明显的拆点。

可是要求从1走到2，再从2走到3，显然不太优点理。由于每一个点最多经过一次，所以从1走到2的路径与2走到3的路径显然是全然不同的两条路径。并且还是无向图，那么最好还是考虑从2出发找两条不同的路径分别走到1和3。这样建图就呼之欲出了：s->2，容量为2;1->t,3->t容量均为1，图中全部边容量均为1，在此图中跑最大流就可以。要注意的是输入中不在区间[1,n]内的点要扔掉。

/*
 *
 * Author : fcbruce <fcbruce8964@gmail.com>
 *
 * Time : Wed 19 Nov 2014 04:39:23 PM CST
 *
 */
#include <cstdio>
#include <iostream>
#include <sstream>
#include <cstdlib>
#include <algorithm>
#include <ctime>
#include <cctype>
#include <cmath>
#include <string>
#include <cstring>
#include <stack>
#include <queue>
#include <list>
#include <vector>
#include <map>
#include <set>
#define sqr(x) ((x)*(x))
#define LL long long
#define itn int
#define INF 0x3f3f3f3f
#define PI 3.1415926535897932384626
#define eps 1e-10

#ifdef _WIN32
  #define lld "%I64d"
#else
  #define lld "%lld"
#endif

#define maxm 65555<<3
#define maxn 33333<<1

using namespace std;

int n,m;

int fir[maxn];
int u[maxm],v[maxm],cap[maxm],flow[maxm],nex[maxm];
int e_max;

int lv[maxn],q[maxn],iter[maxn];

inline void add_edge(int s,int t,int c)
{
  int &e=e_max;
  u[e]=s;v[e]=t;cap[e]=c;
  nex[e]=fir[u[e]];fir[u[e]]=e++;
  u[e]=t;v[e]=s;cap[e]=0;
  nex[e]=fir[u[e]];fir[u[e]]=e++;
}

void dinic_bfs(int s)
{
  int f,r;
  memset(lv,-1,sizeof lv);
  q[f=r=0]=s;
  lv[s]=0;

  while (f<=r)
  {
    int x=q[f++];
    for (int e=fir[x];~e;e=nex[e])
    {
      if (cap[e]>flow[e] && lv[v[e]]<0)
      {
        lv[v[e]]=lv[x]+1;
        q[++r]=v[e];
      }
    }
  }
}

int dinic_dfs(int s,int t,int f)
{
  if (s==t) return f;
  for (int &e=iter[s];~e;e=nex[e])
  {
    if (cap[e]>flow[e] && lv[s]<lv[v[e]])
    {
      int d=dinic_dfs(v[e],t,min(f,cap[e]-flow[e]));
      if (d>0)
      {
        flow[e]+=d;
        flow[e^1]-=d;
        return d;
      }
    }
  }
  return 0;
}

int max_flow(int s,int t)
{
  memset(flow,0,sizeof flow);
  int total_flow=0;
  for (;;)
  {
    dinic_bfs(s);
    if (lv[t]<0) break;

    memcpy(iter,fir,sizeof fir);

    int f;
    while ((f=dinic_dfs(s,t,INF))>0)
      total_flow+=f;
  }

  return total_flow;
}

inline int in(int i)
{
  return i;
}

inline int out(int i)
{
  return i+n;
}

int main()
{
#ifdef FCBRUCE
  freopen("/home/fcbruce/code/t","r",stdin);
#endif // FCBRUCE

  int T_T;
  scanf("%d",&T_T);

  while (T_T--)
  {
    e_max=0;
    memset(fir,-1,sizeof fir);

    scanf("%d%d",&n,&m);

    int s=0,t=n*2+2;
    add_edge(s,out(2),2);
    add_edge(in(1),t,1);
    add_edge(in(3),t,1);
    for (int i=4;i<=n;i++) add_edge(in(i),out(i),1);
    for (int i=0,u,v;i<m;i++)
    {
      scanf("%d%d",&u,&v);
      if (u<1 || u>n || v<1 || v>n) continue;
      add_edge(out(u),in(v),1);
      add_edge(out(v),in(u),1);
    }

    if (max_flow(s,t)==2) puts("YES");
    else puts("NO");
  }

  return 0;
}