bzoj2687: 交与并

Description

    对于一个区间集合{A1,A2……AK}(K>1，Ai<>Aj{i<>j})，我们定义其权值
           W=|A1∪A2∪……∪AK|*|A1∩A2∩……AK|

     当然，如果这些区间没有交集则权值为0。

Input

    给你N个各不相同的区间，请你从中找出若干个区间使其权值最大。

第一行N

接下来N行 l r(1<=l<r<=10^6)

Output

最大权值

Sample Input

4

1 6

4 8

2 7

3 5

Sample Output

24

样例注释:选择第1个和第3个区间,交为(2,6),并为(1,7),
权值为4*6=24.

HINT

100%  1<N<=10^6

题解：

选出的最优区间集合满足下列性质：

1.交集肯定不能为空。

2.设这个区间集合的并集为U，对于任意一个区间，设这个区间集合去掉这个区间的并集为U'，满足U'⫋U。

第一条显然。。。

第二条：假如去掉这个集合后并集没有减小，去掉后显然交集不会减小，所以答案也不会变小。

所以选出来的集合只有一个区间或两个互不包含的区间。

由于集合大小不能为1，所以只能选两个区间。

首先我们将区间按左端点从小到大，如果左端点相同，则按右端点从大到小的顺序排好序。

对于其中一个区间含于另一个区间的情况：显然包含它的区间只能在他前面，而且具有单调性，所以用个单调队列维护一下即可。

对于两个互不包含的区间的情况：先将含于其他区间的区间去掉，这时区间的左右端点都单调上升，然后有一个性质：

假如第i-1个区间选择的最优区间为第k个（k<i-1），第i个区间选择的最优区间为第j个（j<i），则有k<=j

证明：

假设j<k，对于i，有：

同理，对于i-1（记作i'），有：

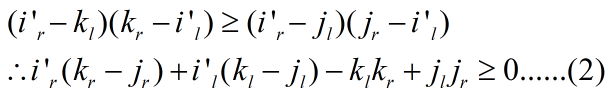
所以假设不成立，所以有k<=j，这样就有决策单调性了，用栈来维护一下即可。

code:

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 char ch;
 bool ok;
 void read(int &x){
     for (ok=,ch=getchar();!isdigit(ch);ch=getchar()) if (ch=='-') ok=;
     for (x=;isdigit(ch);x=x*+ch-'',ch=getchar());
     if (ok) x=-x;
 }
 const int maxn=;
 typedef long long int64;
 int n,cnt,last;
 int64 ans;
 struct Seg{
     int l,r;
 }seg[maxn];
 inline bool cmp(const Seg &a,const Seg &b){return (a.l<b.l)||(a.l==b.l&&a.r>b.r);}
 inline int64 calc(const Seg &j,const Seg &i){return 1LL*(i.r-j.l)*(j.r-i.l);}
 struct Stack{
     int top,pos;
     struct Data{
         int l,r,id;
     }s[maxn],tmp;
     void init(){s[top=]=(Data){,n,},pos=;}
     bool cmp(int a,int x,int y){return calc(seg[x],seg[a])<calc(seg[y],seg[a]);}
     int get(int id){
         int l=tmp.l,r=tmp.r,m,a=tmp.id;
         while (l<r){
             m=((l+r)>>)+;
             if (cmp(m,a,id)) l=m; else r=m-;
         }
         return l;
     }
     void push(int id){
         while (top&&!cmp(s[top].l,s[top].id,id)) top--;
         tmp=s[top--];
         int m=get(id);
         if (tmp.l<=m) s[++top]=(Data){tmp.l,m,tmp.id};
         if (m<n) s[++top]=(Data){m+,n,id};
     }
     int64 query(int x){
         while (x>s[pos].r) pos++;
         return calc(seg[s[pos].id],seg[x]);
     }
 }stack;
 struct Que{
     int head,tail;
     struct Data{
         int r,len;
     }q[maxn],tmp;
     void init(){head=,tail=;}
     void push(int id){
         tmp=(Data){seg[id].r,seg[id].r-seg[id].l};
         while (head<=tail&&q[tail].len<=tmp.len) tail--;
         q[++tail]=tmp;
     }
     int64 query(int id){
         int r=seg[id].r;
         while (head<=tail&&q[head].r<r) head++;
         if (head<=tail) return q[head].len;
         else return -;
     }
 }que;
 int main(){
     read(n);
     for (int i=;i<=n;i++) read(seg[i].l),read(seg[i].r);
     sort(seg+,seg+n+,cmp),que.init();
     for (int i=;i<=n;i++)
         if (seg[i].r>last) last=seg[i].r,seg[++cnt]=seg[i],que.push(i);
         else ans=max(ans,que.query(i)*(seg[i].r-seg[i].l));
     n=cnt,stack.init();
     for (int i=;i<=n;i++) ans=max(ans,stack.query(i)),stack.push(i);
     printf("%lld\n",ans);
     return ;
 }