用硬件（Verilog）实现二进制码和格雷码的转换

格雷码(Gray code)是1880年由法国工程师Jean-Maurice-Emlle Baudot发明的一种编码，是一种绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码，是一种错误最小化的编码方式，因为，虽然自然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况，例如从十进制的3转换为4时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻位间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同，引起数字量发生变化时，格雷码仅改变一位，这样与其它编码同时改变两位或多位的情况相比更为可靠，即可减少出错的可能性。

格雷码是一个数列集合，相邻两数间只有一个位元改变，为无权数码，且格雷码的顺序不是唯一 的。
     格雷码的构造方法为：直接排列以二进制为0值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反覆，即可排列出n个位元的格雷码。

下面主要谈谈格雷码和自然二进制码之间的转换方法。

1）自然二进制码转换为格雷码的方法

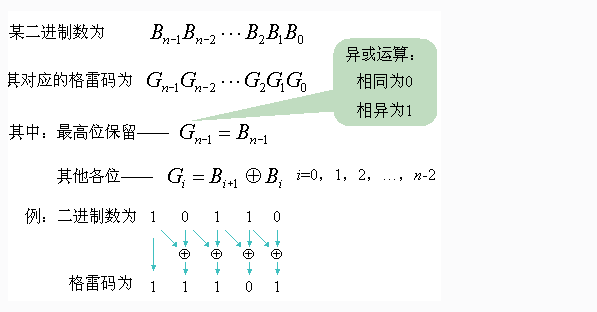
自然二进制码转换成二进制格雷码，其法则是保留自然二进制码的最高位作为格雷码的最高位，而次高位格雷码为二进制码的高位与次高    位相异或，而格雷码其余各位与次高位的求法相类似。

    原理: 若二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0];

         相应地, 则二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0].

         其中最高位保留: G[N-1] = B[N-1];

         其他各位: G[i] = B[i+1] xor B[i]. (i = 0, 1, 2, ..., n-2)

    图示如下：

bin[3]    bin[2]     bin[1]      bin[0]          ---二进制值 ： 二进制

+     0     bin[3]     bin[2]      bin[1]          ---右移值（二进制）

---

gray[3]  gray[2]    gray[1]    gray[0]      ---对应的格雷码值

总结：格雷码的值只需要在原来的二进制的基础上右移一位再加上原来的二进制值即可得到。

其实现代码如下：

module bin2gry(Gry,Bin);
parameter length = ;     //以八位示例
output [length-:] Gry;
input [length-:] Bin;

reg [length-:] Gry;
integer i;

always @ (Bin)
begin
    for(i=;i<length-;i=i+1)
        Gry[i]=Bin[i]^Bin[i+];
    Gry[i]=Bin[i];
end

/*另一种简单的实现方法如下：*/
// assign Gray = (Bin >> 1) ^ Bin;
endmodule

 

仿真波形

图1. length ="3"

图2. length ="4"

2）格雷码转换为二进制码的实现方法

二进制格雷码转换成自然二进制码,其法则是保留格雷码的最高位作为自然二进制码的最高位，而次高位自然二进制码为高位自然二进制       码与次高位格雷码相异或，而自然二进制码的其余各位与次高位自然二进制码的求法相类似。

    原理: 若二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0];

         相应地, 则二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0].

         其中最高位保留: B[N-1] = G[N-1];

         其他各位: B[i-1] = G[i-1] xor B[i]. (i = 1, 2, ..., n-1)

    图示如下：

  

 用代码实现如下：

module gry2bin(Gry,Bin);
parameter length = ;
input [length-:] Gry;
output [length-:] Bin; 

reg [length-:] Bin;
integer i;
always @ (Gry)
begin
    Bin[length-]=Gry[length-];
    for(i=length-;i>=;i=i-1)
        Bin[i]=Bin[i+]^Gry[i];
end
endmodule

 

仿真波形

 

图3. length="3"

 

图4. length="4"