拉普拉斯特征图降维及其python实现
这种方法假设样本点在光滑的流形上,这一方法的计算数据的低维表达,局部近邻信息被最优的保存。以这种方式,可以得到一个能反映流形的几何结构的解。
步骤一:构建一个图G=(V,E),其中V={vi,i=1,2,3…n}是顶点的集合,E={eij}是连接顶点的vi和vj边,图的每一个节点vi与样本集X中的一个点xi相关。如果xi,xj相距较近,我们就连接vi,vj。也就是说在各自节点插入一个边eij,如果Xj在xi的k领域中,k是定义参数。
步骤二:每个边都与一个权值Wij相对应,没有连接点之间的权值为0,连接点之间的权值:
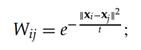
步骤三:令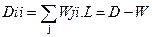 ,实现广义本征分解:
,实现广义本征分解:
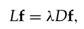
使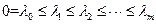 是最小的m+1个本征值。忽略与
是最小的m+1个本征值。忽略与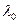 =0相关的本征向量,选取另外m个本征向量即为降维后的向量。
=0相关的本征向量,选取另外m个本征向量即为降维后的向量。
2.1、python实现拉普拉斯降维
def laplaEigen(dataMat,k,t):
m,n=shape(dataMat)
W=mat(zeros([m,m]))
D=mat(zeros([m,m]))
for i in range(m):
k_index=knn(dataMat[i,:],dataMat,k)
for j in range(k):
sqDiffVector = dataMat[i,:]-dataMat[k_index[j],:]
sqDiffVector=array(sqDiffVector)**2
sqDistances = sqDiffVector.sum()
W[i,k_index[j]]=math.exp(-sqDistances/t)
D[i,i]+=W[i,k_index[j]]
L=D-W
Dinv=np.linalg.inv(D)
X=np.dot(D.I,L)
lamda,f=np.linalg.eig(X)
return lamda,f
def knn(inX, dataSet, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize,1)) - dataSet
sqDiffMat = array(diffMat)**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
return sortedDistIndicies[0:k]
dataMat, color = make_swiss_roll(n_samples=2000)
lamda,f=laplaEigen(dataMat,11,5.0)
fm,fn =shape(f)
print 'fm,fn:',fm,fn
lamdaIndicies = argsort(lamda)
first=0
second=0
print lamdaIndicies[0], lamdaIndicies[1]
for i in range(fm):
if lamda[lamdaIndicies[i]].real>1e-5:
print lamda[lamdaIndicies[i]]
first=lamdaIndicies[i]
second=lamdaIndicies[i+1]
break
print first, second
redEigVects = f[:,lamdaIndicies]
fig=plt.figure('origin')
ax1 = fig.add_subplot(111, projection='3d')
ax1.scatter(dataMat[:, 0], dataMat[:, 1], dataMat[:, 2], c=color,cmap=plt.cm.Spectral)
fig=plt.figure('lowdata')
ax2 = fig.add_subplot(111)
ax2.scatter(f[:,first], f[:,second], c=color, cmap=plt.cm.Spectral)
plt.show()
2.2、拉普拉斯降维实验
用如下参数生成实验数据存在swissdata.dat里面:
def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):
#Generate a swiss roll dataset.
t = 1.5 * np.pi * (1 + 2 * random.rand(1, n_samples))
x = t * np.cos(t)
y = 83 * random.rand(1, n_samples)
z = t * np.sin(t)
X = np.concatenate((x, y, z))
X += noise * random.randn(3, n_samples)
X = X.T
t = np.squeeze(t)
return X, t
实验结果如下:
N=5,t=15: N=7,t=15: N=9,t=15:
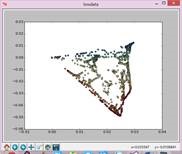
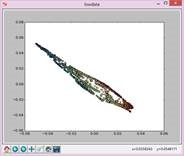
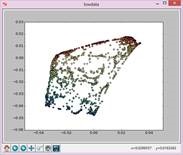
N=11,t=15: N=13,t=15: N=15,t=15:
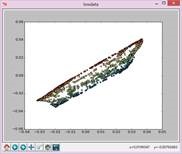
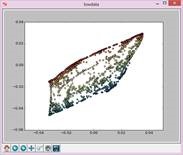
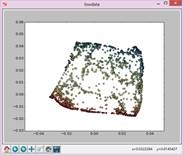
N=17,t=15: N=19,t=15: N=21,t=15:
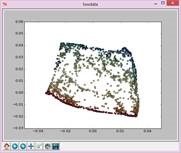
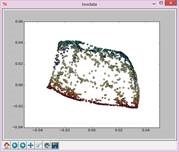
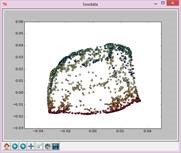
N=23,t=15: N=25,t=15: N=27,t=15:
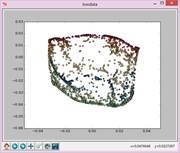
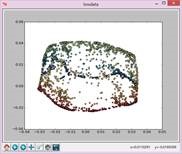
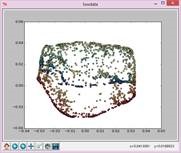
N=29,t=15: N=31,t=15: N=33,t=15:
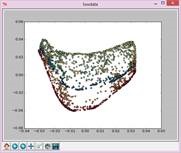
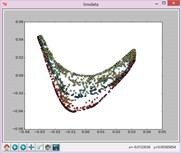
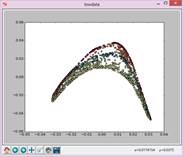
N=25,t=5: N=25,t=8: N=25,t=10:
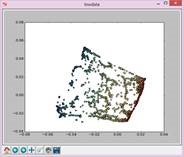
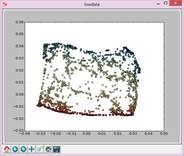

N=25,t=12: N=25,t=14: N=25,t=50:
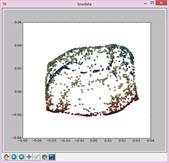
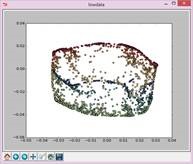
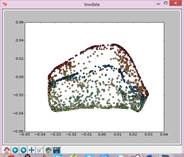
N=25,t=Inf:
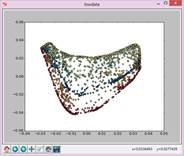
拉普拉斯特征图降维及其python实现的更多相关文章
- LBP特征学习(附python实现)
LBP的全称是Local Binary Pattern即局部二值模式,是局部信息提取中的一种方法,它具有旋转不变性和灰度不变性等显著的优点.在人脸识别领域有很多案例,此外,局部特征的算法还有 SIFT ...
- 拉普拉斯特征映射(Laplacian Eigenmaps)
1 介绍 拉普拉斯特征映射(Laplacian Eigenmaps)是一种不太常见的降维算法,它看问题的角度和常见的降维算法不太相同,是从局部的角度去构建数据之间的关系.也许这样讲有些抽象,具体来讲, ...
- GhostNet: 使用简单的线性变换生成特征图,超越MobileNetV3的轻量级网络 | CVPR 2020
为了减少神经网络的计算消耗,论文提出Ghost模块来构建高效的网络结果.该模块将原始的卷积层分成两部分,先使用更少的卷积核来生成少量内在特征图,然后通过简单的线性变化操作来进一步高效地生成ghost特 ...
- 以图搜图(一):Python实现dHash算法(转)
近期研究了一下以图搜图这个炫酷的东西.百度和谷歌都有提供以图搜图的功能,有兴趣可以找一下.当然,不是很深入.深入的话,得运用到深度学习这货.Python深度学习当然不在话下. 这个功能最核心的东西就是 ...
- 卷积神经网络特征图可视化(自定义网络和VGG网络)
借助Keras和Opencv实现的神经网络中间层特征图的可视化功能,方便我们研究CNN这个黑盒子里到发生了什么. 自定义网络特征可视化 代码: # coding: utf-8 from keras.m ...
- Keras中间层输出的两种方式,即特征图可视化
训练好的模型,想要输入中间层的特征图,有两种方式: 1. 通过model.get_layer的方式.创建新的模型,输出为你要的层的名字. 创建模型,debug状态可以看到模型中,base_model/ ...
- 卷积网络中的通道(Channel)和特征图
转载自:https://www.jianshu.com/p/bf8749e15566 今天介绍卷积网络中一个很重要的概念,通道(Channel),也有叫特征图(feature map)的. 首先,之前 ...
- SLAM概念学习之特征图Feature Maps
特征图(或者叫地标图,landmark maps)利用参数化特征(如点和线)的全局位置来表示环境.如图1所示,机器人的外部环境被一些列参数化的特征,即二维坐标点表示.这些静态的地标点被观测器(装有传感 ...
- 深度学习之加载VGG19模型获取特征图
1.加载VGG19获取图片特征图 # coding = utf-8 import tensorflow as tf import numpy as np import matplotlib.pyplo ...
随机推荐
- 笨方法学python 33课
今天Eiffel看到了第33章,任务是把一个while循环改成一个函数. 我在把while循环改成函数上很顺利,但是不知道怎么写python的主函数,在参数的调用上也出现了问题. 通过查资料,发现py ...
- 制作Mac OS X Mavericks 安装U盘
1. 8G+ U盘一个. 2. App Store 下载Maverics到本地(默认会下载到Applications) 2. 打开Mac OS 磁盘工具(Disk Utility),左侧选中U盘,在右 ...
- jquery 验证插件 validate
1)required:true 必输字段(2)remote:"check.php" 使用ajax方法调用check.php验证输入值(3)email:true 必须输入正确格式的电 ...
- csv转json文件
今天因为需要帮一个同事的新闻内容录入为html, 每次手改不方便,所以就弄了个csv(excel)转json的c++程序,然后再利用ejs把它渲染成网页,打开渲染好的网页再保存(不能保存源文件,不然还 ...
- MVC去掉传参时的验证:从客户端中检测到有潜在危险的Request.QueryString值
解决方法:给Action添加属性[ValidateInput(false)]. 例: [ValidateInput(false)] public ActionResult Index(string o ...
- homework-Agile Software Development
对敏捷开发的一些思考 这周的作业是对敏捷开发的相关阅读和思考. 在阅读的过程中,可以看到作者是一位具有丰富编程经验的大师.在开发的经历中,作者经历了极限编程等开发过程,但是在作者的多年经验中,作者还是 ...
- 使用WampServer 3.0
在server上安装了WampServer 发现本地使用良好,但是无法从别的PC访问. 原因有二: 1.现象:输入连接无反应 原因:server本身用了80端口,所有WampServer我就设置了80 ...
- firefox浏览器删除插件
打开注册表编辑器([开始菜单]→[运行]或 Win+R快捷键打开运行,输入regedit). 2 点击菜单栏[编辑]→[搜索],或者按 Ctrl + F 快捷键,搜索 MozillaPlugins . ...
- JDBC之PreparedStatement模糊查询
今天要做一个关于模糊查询的需求,以前用JDBC做精确查询都是用 "SELECT * FROM test WHERE id = ?",所以用模糊查询时理所当然的也用了"SE ...
- USB CDC类
现代嵌入式系统中,异步串行通信接口往往作为标准外设出现在单片机和嵌入式系统中.但是随着个人计算机通用外围设备越来越少地使用串口,串口正在逐渐从个人计算机特别是便携式电脑上消失.于是嵌入式开发人员常常发 ...
