《Linear Algebra and Its Applications》-chaper3-行列式-行列式初等变换

承接上一篇文章对行列式的引入，这篇文章将进一步记录关于行列式的有关内容，包括如下的几个方面：

(1)行列式3个初等变换的证明。

(2)转置行列式与原行列式相等的证明。

(3)定理det(AB) = det(A)det(B)的证明。

(4)基于行列式初等变换的范德蒙德行列式的证明。

首先值得说明的是，先前我们介绍矩阵的时候，并没有给出矩阵行变换的相关证明，其实按道理讲它的根源是出自于这里的。行列式和矩阵是有着紧密的联系的，想在这本书中就是基于矩阵的方法来完成对行列式3个初等变换的证明的。

行列式3个初等变换的证明:

图片中给出的证明过程紧凑间接，无需笔者赘言。在这里之所以采用了基于初等矩阵E的方法，便在于矩阵A与E的乘法运算刚好能够反映这3个初等变换。

转置行列式与原行列式相等的证明：

这个问题其实十分简单，但是我们应该能够意识到这个定理的意义，它使得行变换和列变换具有了等价性，也就是说对行适用的变换方式对列都是适用的。

简略的证明过程：定义行列式A并写出其转置矩阵A^T。

将A行列式按照第i行打开，将A^T行列式按照第i列打开，随后可由转置矩阵的定义，完成证明。

det(AB) = det(A)det(B)：

关于这个定理，笔者先前缺少了一些补充知识例如“可逆矩阵的性质”，这是推导过程中|A| = |Ep|…|E2||E1|这一步转化的重要依据。笔者会在抽空将这一转化过程的基本原理。

最后是关于范德蒙德行列式的证明过程。

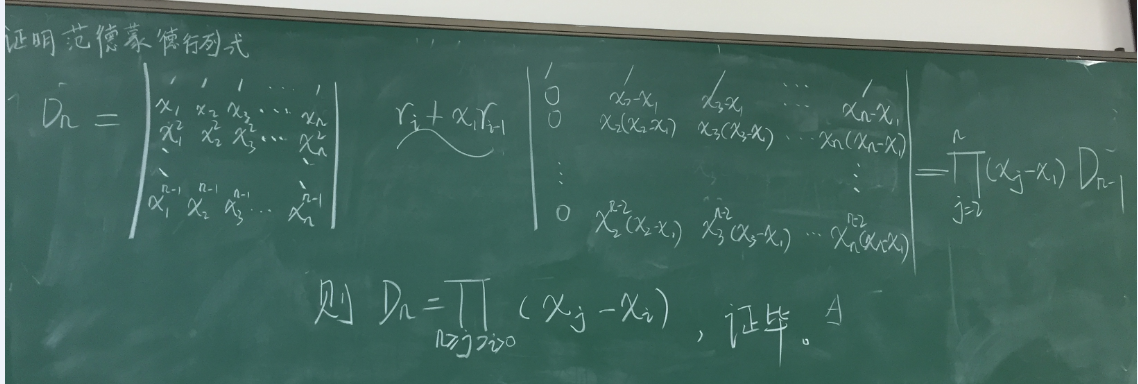
证明过程本身是很简单的，但是它所用到的递归思维是我们在解决其他问题的时候可以借鉴的。