湖南集训day2

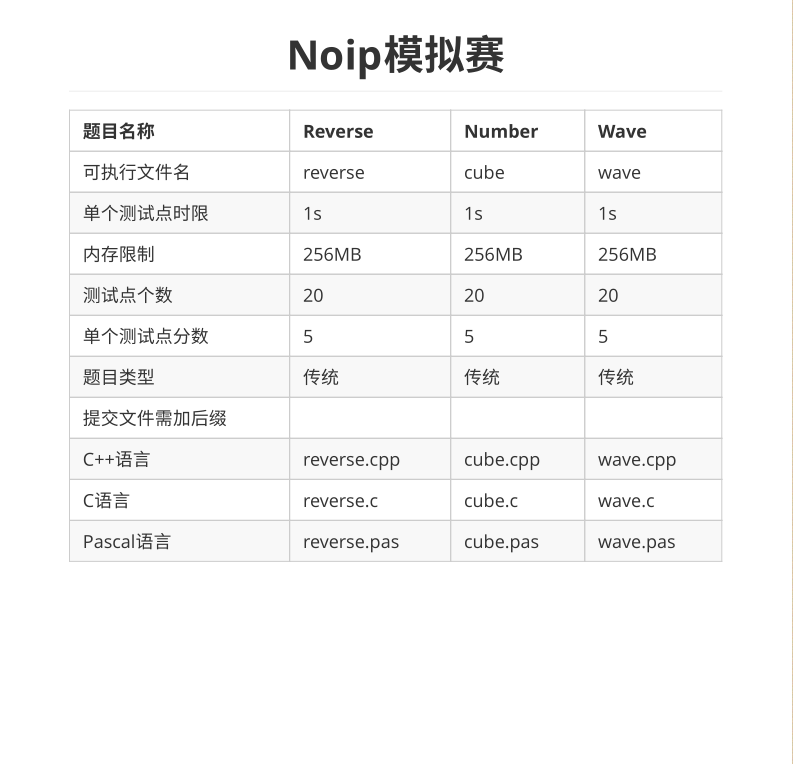
难度:☆☆

/*显然可以前缀和*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 100007

using namespace std;
int n,m,ans,cnt;
int a[N],sum[N];char s[N];

int main()
{
    freopen("reverse.in","r",stdin);
    freopen("reverse.out","w",stdout);
    scanf("%s",s);n=strlen(s);ans=N+N;
    if(n==)
    {
        printf("0\n");
        return ;
    }
    for(int i=;i<n;i++) a[i+]=s[i]==''?:;
    for(int i=;i<=n;i++) sum[i]=sum[i-]+a[i];
    for(int i=;i<=n;i++)
    {
        ans=min(ans,sum[i]+n-i-(sum[n]-sum[i]));
    }
    printf("%d\n",ans);
    return ;
}

/*
枚举，用vis一个二进制数组表示当前数每一位的状态，出现或者不出现。
然后把二进制转为十进制，cnt[十进制]+1。
最后因为要求多少对，所以答案累加C(i,2)。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define size 1024

using namespace std;
int n,cnt[size],vis[];
int Use[]={,,,,,,,,,};
long long ans;

int main()
{
    freopen("number.in","r",stdin);
    freopen("number.out","w",stdout);
    cin>>n;
    int start,End;
    for(int i=;i<=n;i++)
    {
        start=i;End=;memset(vis,,sizeof vis);
        while(start) vis[start%]=,start/=;
        for(int j=;j<=;j++) if(vis[j]) End+=Use[j];
        cnt[End]++;
    }
    for(int i=;i<size;i++) ans+=1ll*cnt[i]*(cnt[i]-)/;
    cout<<ans<<endl;
    fclose(stdin);fclose(stdout);
    return ;
}

/*
做法类似最长上升子序列
线段树可以优化到70，不会写没治...
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>

#define N 10000007

using namespace std;
int dp[N],a[N],cnt[N];
int n,k,ans;

int main()
{
    freopen("wave14.in","r",stdin);
    freopen("wave.out","w",stdout);
    scanf("%d%d",&n,&k);
    for(int i=;i<=n;i++) scanf("%d",&a[i]);
    for(int i=;i<=n;i++) dp[i]=cnt[i]=;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=i;j++)
        {
            if(abs(a[j]-a[i])>=k)
            {
                if(cnt[j]%== && a[i]<a[j])
                {
                     if(dp[i]<dp[j]+) dp[i]=dp[j]+,cnt[i]=cnt[j]+;
                }
                else if(cnt[j]%!= && a[i]>=a[j])
                {
                     if(dp[i]<dp[j]+) dp[i]=dp[j]+,cnt[i]=cnt[j]+;
                }
                else dp[i]=max(dp[i],dp[j]);
            }
        }
    }
    printf("%d\n",dp[n]);
    fclose(stdin);fclose(stdout);
    return ;
}

30分暴力dp

/*
很神奇。
贪心，在满足k的限制下，偶数项尽量大，奇数项尽量小。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 2000007

using namespace std;
int a[N];
int n,k,m,ans,cur;

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

int main()
{
    n=read();k=read();
    for(int i=;i<n;i++) a[i]=read();
    ans=,m=,cur=a[];
    for(int i=;i<n;i++)
    {
        if(m)
          if(cur-a[i]>=k)
            m=,ans++,cur=a[i];
          else cur=max(cur,a[i]);

        else
          if(a[i]-cur>=k)
            m=,ans++,cur=a[i];
          else cur=min(cur,a[i]);
    }
    printf("%d\n",ans);
    return ;
}