HDU 5402 Travelling Salesman Problem（多校9 模拟）

题目链接：

pid=5402">http://acm.hdu.edu.cn/showproblem.php?pid=5402

题意：给出一个n×m的矩阵，位置（i。j）有一个非负权值。

每一个点仅仅能经过一次。求从（1。1）到（n。m）权值总和最大的和。还需输出路径。

思路：由于走的点越多越好，所以得到规律，当n，m随意一个为奇数时。均能够走全然部点。

当n，m全为偶数时，当点（i。j）的i和j不同奇偶时，则除了（i，j）这个点均能够走完剩下的全部点。

剩下模拟就可以。

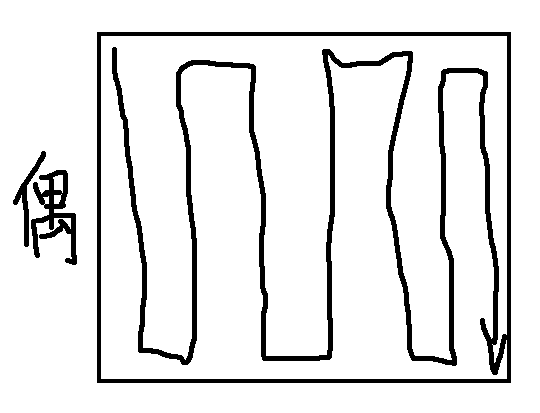
1. n，m当中一个为奇数的时候，相似下图走法就可以。顺着偶数边走，若均为奇数，则随意都可。
2. n。m均为偶数，先找出最小的位置（ni，nj）且ni和nj奇偶不同的位置（下图中（ni，nj）为黑点位置）。
   
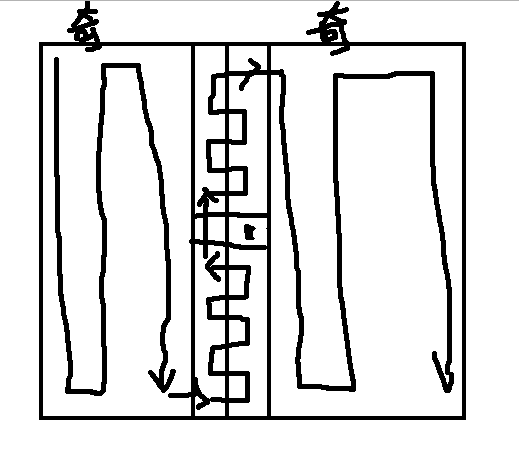
   1. 假设nj为奇数，相似下图走法就可以。
   2. 假设nj为偶数，相似下图走法就可以。
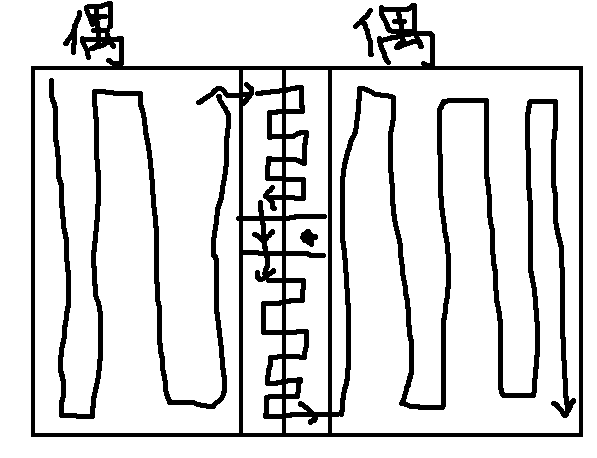
   3. 特别的是nj为1的时候由于不能向左分出一列。所以向右分出一列。特判就可以。

代码。

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <queue>
#include <string>
#include <math.h>
using namespace std;

const int N = 1e2 + 10;

void out(int n, int m, char a, char b, char c) {
    for (int i = 1; i <= n; i++) {
        if (i > 1) printf("%c", a);
        for (int j = 1; j < m; j++) {
            if (i & 1) printf("%c", b);
            else printf("%c", c);
        }
    }
}

int main() {
    int n, m;
    while (scanf("%d%d", &n, &m) != EOF) {
        int ans = 0, tmp = 10005;
        int ni, nj;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                int x;
                scanf("%d", &x);
                ans += x;
                if (((i + j) & 1) && x < tmp) {
                    tmp = x;
                    ni = i;
                    nj = j;
                }
            }
        }
        if (n % 2 == 0 && m % 2 == 0)
            ans -= tmp;
        printf("%d\n", ans);
        if (n & 1) {
            out(n, m, 'D', 'R', 'L');
        }
        else if (m & 1) {
            out(m, n, 'R', 'D', 'U');
        }
        else {
            if (nj == 1) {
                if (ni - 1 > 0) {
                    out(ni - 1, 2, 'D', 'R', 'L');
                    printf("D");
                }
                if (ni < n) {
                    printf("D");
                    out(n - ni, 2, 'D', 'L', 'R');
                }
                if (m > 2) {
                    printf("R");
                    out(m - 2, n, 'R', 'U', 'D');
                }
                printf("\n");
                continue;
            }
            if (nj & 1) {
                if (nj - 2 > 0) {
                    out(nj - 2, n, 'R', 'D', 'U');
                    printf("R");
                }
                if (n - ni > 0) {
                    out(n - ni, 2, 'U', 'R', 'L');
                    printf("U");
                }
                if (ni - 1 > 0) {
                    printf("U");
                    out(ni - 1, 2, 'U', 'R', 'L');
                }
                if (m - nj > 0) {
                    printf("R");
                    out(m - nj, n, 'R', 'D', 'U');
                }
            }
            else {
                if (nj - 2 > 0) {
                    out(nj - 2, n, 'R', 'D', 'U');
                    printf("R");
                }
                if (ni - 1 > 0) {
                    out(ni - 1, 2, 'D', 'R', 'L');
                    printf("D");
                }
                if (ni < n) {
                    printf("D");
                    out(n - ni, 2, 'D', 'R', 'L');
                }
                if (m - nj > 0) {
                    printf("R");
                    out(m - nj, n, 'R', 'U', 'D');
                }
            }
        }
        printf("\n");
    }
    return 0;
}