BZOJ 3384 上帝与集合的正确用法

上帝与集合的正确用法

【问题描述】

【输入格式】

第一行一个T，接下来T行，每行一个正整数p，代表你需要取模的值。

【输出格式】

T行，每行一个正整数，为答案对p取模后的值。

【样例输入】

3
2
3
6

【样例输出】

0
1
4

【数据范围】

对于100%的数据，T<=1000，p<=10^7

---

题解：

 

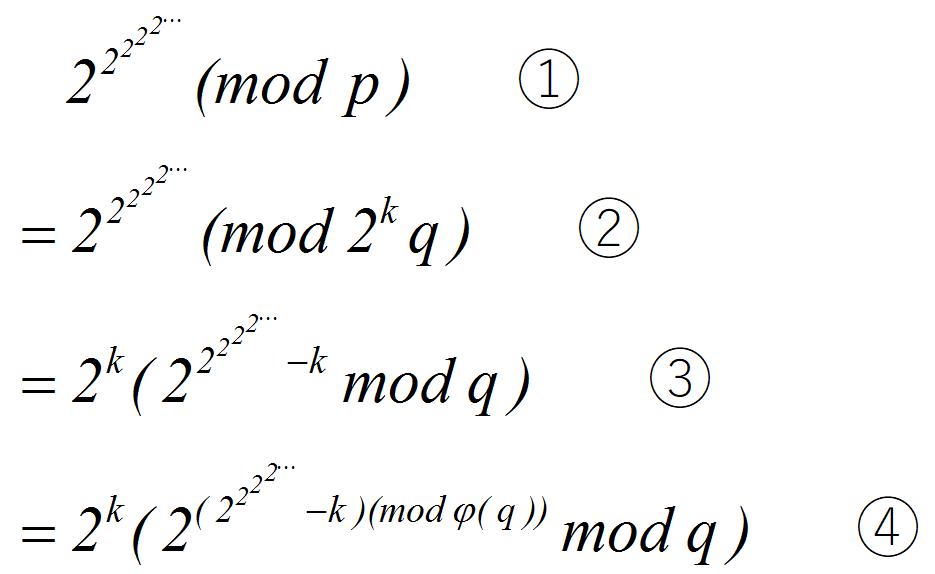
①->②：把模数 p 拆成 2^kq 的形式，其中 q 是奇数

②->③：

将上式左右同除以2^k

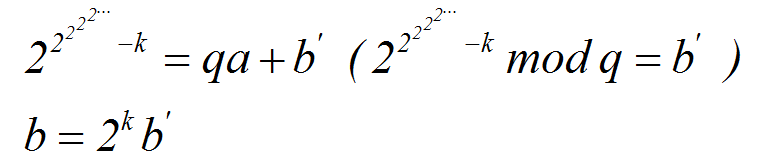
不会同余的蒟蒻只能这么推了

③->④:

此时 q 是奇数，必定与 2ⁿ 互质

则套用欧拉定理

考虑一个数的 phi 必定比它本身的值小

那么如此递归下去模数会变为 1，则返回 0

回溯得到答案

 #include<cmath>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 int n;
 inline void Scan(int &x)
 {
     char c;
     bool o = false;
     while(!isdigit(c = getchar())) o = (c != '-') ? o : true;
     x = c - '';
     while(isdigit(c = getchar())) x = x *  + c - '';
     if(o) x = -x;
 }
 int Phi(int x)
 {
     int ans = x;
     for(int i = ; i * i <= x; ++i)
     {
         if(!(x % i))
         {
             while(!(x % i)) x /= i;
             ans /= i, ans *= (i - );
         }
     }
     if(x ^ ) ans /= x, ans *= (x - );
     return ans;
 }
 int Pow(int x, int n, int mod)
 {
     int sum = ;
     while(n)
     {
         if(n & ) sum = (long long) sum * x % mod;
         x = (long long) x * x % mod;
         n >>= ;
     }
     return sum % mod;
 }
 int Work(int p)
 {
     if(p == ) return ;
     int k = ;
     while(!(p & )) p >>= , ++k;
     int phi = Phi(p);
     int s = (Work(phi) - k) % phi;
     if(s < ) s += phi;
     return Pow(, s, p) << k;
 }
 int main()
 {
     Scan(n);
     int p;
     for(int i = ; i <= n; ++i)
     {
         Scan(p);
         printf("%d\n", Work(p));
     }
 }