POJ1692 Crossed Matchings

Time Limit: 1000MS

		Memory Limit: 10000K
Total Submissions: 2738		Accepted: 1777

Description

There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment.


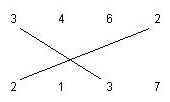
We want to find the maximum number of matching segments possible to draw for the given input, such that:

1. Each a-matching segment should cross exactly one b-matching segment, where a != b .

2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed.



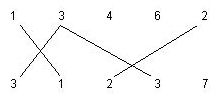
Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

Input

The
first line of the input is the number M, which is the number of test
cases (1 <= M <= 10). Each test case has three lines. The first
line contains N1 and N2, the number of integers on the first and the
second row respectively. The next line contains N1 integers which are
the numbers on the first row. The third line contains N2 integers which
are the numbers on the second row. All numbers are positive integers
less than 100.

Output

Output
should have one separate line for each test case. The maximum number of
matching segments for each test case should be written in one separate
line.

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3
1 1 3 3
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3

Sample Output

6
0
8

Source

Tehran 1999

两个交叉的匹配为一组，每找到一组可行的匹配，答案数+2 。

设：f[上方匹配位置][下方匹配位置]=最优解

假设现在扫到了上方数组的i点和下方数组的j点。首先可以想到如果没有新的匹配，f[i][j]=max(f[i][j-1],f[i-1][j])

接着考虑新的匹配，在上方数组中从i往前找，找到最近的pos1使a[pos1]=b[j]，同理在下方找到b[pos2]=a[i]，那么pos1-j,pos2-i两条连线必然交叉，得到动归方程：

f[i][j]=max(f[i][j],f[pos1-1][pos2-1]+2)

 /**/
 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int mxn=;
 int n1,n2;
 int a[mxn],b[mxn];
 int f[mxn][mxn];
 int main(){
     int T;
     scanf("%d",&T);
     int i,j;
     while(T--){
         memset(f,,sizeof f);
         scanf("%d%d",&n1,&n2);
         for(i=;i<=n1;i++)scanf("%d",&a[i]);
         for(i=;i<=n2;i++)scanf("%d",&b[i]);
         for(i=;i<=n1;i++)
           for(j=;j<=n2;j++){
               f[i][j]=max(f[i][j-],f[i-][j]);
               if(a[i]==b[j])continue;
               int k=i-;
               while(k && a[k]!=b[j])k--;int pos1=k;
               k=j-;
               while(k && b[k]!=a[i])k--;int pos2=k;
               if(pos1&&pos2)  f[i][j]=max(f[i][j],f[pos1-][pos2-]+);
             }
         printf("%d\n",f[n1][n2]);
     }
     return ;
 }