LCS最大公共子序列【转载】

在两个字符串中，有些字符会一样，可以形成的子序列也有可能相等，因此，长度最长的相等子序列便是两者间的最长公共字序列，其长度可以使用动态规划来求。

以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。

借用《算法导论》中的推导图：

创建 DP数组C[][];

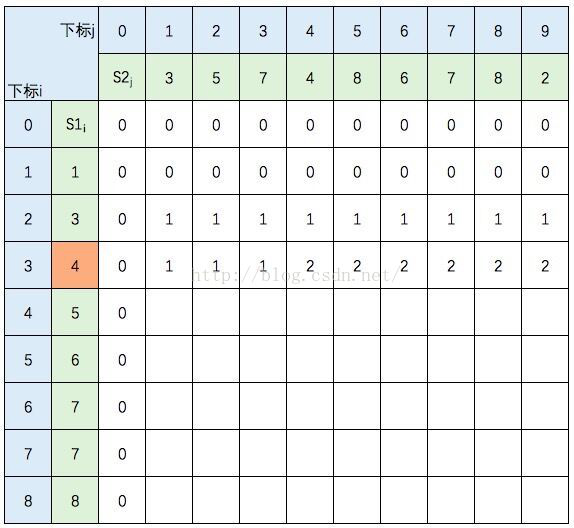
图中的空白格子需要填上相应的数字（这个数字就是c[i][j]的定义，记录的LCS的长度值）。填的规则依据递归公式，简单来说：如果横竖（i,j）对应的两个元素相等，该格子的值 = c[i-1,j-1] + 1。如果不等，取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表：

然后，一行一行地从上往下填：

S1的元素3 与 S2的元素3 相等，所以 c[2,1] = c[1,0] + 1。继续填充：

S1的元素3 与 S2的元素5 不等，c[2,2] =max(c[1,2],c[2,1])，图中c[1,2] 和 c[2,1] 背景色为浅黄色。

继续填充：

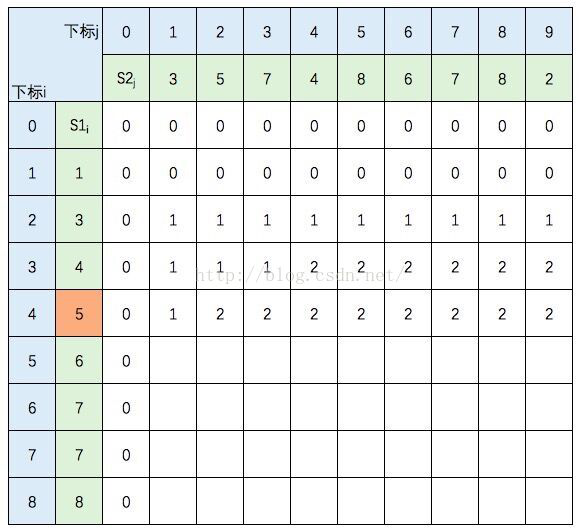
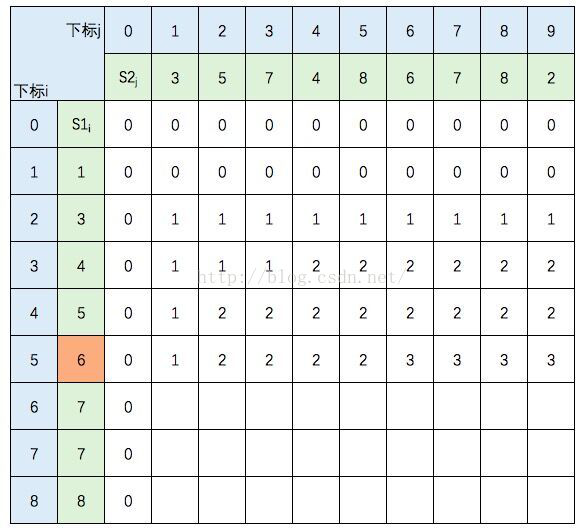
中间几行填写规则不变，直接跳到最后一行：

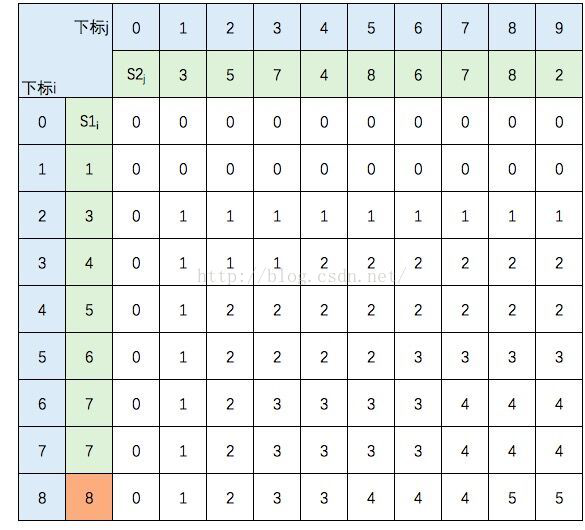
至此，该表填完。根据性质，c[8,9] = S1 和 S2 的 LCS的长度，即为5。

得到公式

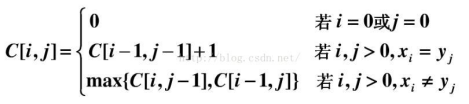
代码

#include<iostream>

#include<cstdio>

#include<cstring>

#include<string>

using namespace std;

const int MAXN = 1005;

int DP[MAXN][MAXN];

int main()

{

string a;

string b;

while(cin >> a >> b)

{

int l1 = a.size();

int l2 = b.size();

memset(DP, 0, sizeof(DP));

for(int i = 1; i <= l1; i++)

for(int j = 1; j <= l2; j++)

if(a[i - 1] == b[j - 1])

DP[i][j] = max(DP[i][j], DP[i - 1][j - 1] + 1);

else

DP[i][j] = max(DP[i][j - 1], DP[i - 1][j]);

printf("%d\n", DP[l1][l2]);

}

return 0;

}

当得到完整的DP表之后，我们可以通过倒推来得到相应的子序列

S1和S2的最LCS并不是只有1个，本文并不是着重讲输出两个序列的所有LCS，只是介绍如何通过上表，输出其中一个LCS。

我们根据递归公式构建了上表，我们将从最后一个元素c[8][9]倒推出S1和S2的LCS。

c[8][9] = 5，且S1[8] != S2[9]，所以倒推回去，c[8][9]的值来源于c[8][8]的值(因为c[8][8] > c[7][9])。

c[8][8] = 5,  且S1[8] = S2[8], 所以倒推回去，c[8][8]的值来源于 c[7][7]。

以此类推，如果遇到S1[i] != S2[j] ，且c[i-1][j] = c[i][j-1] 这种存在分支的情况，这里请都选择一个方向（之后遇到这样的情况，也选择相同的方向）。

第一种结果为：

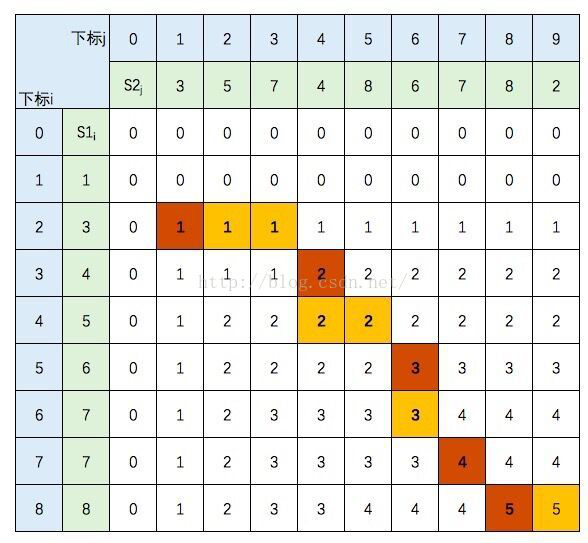
这就是倒推回去的路径，棕色方格为相等元素，即LCS = {3,4,6,7,8}，这是其中一个结果。

如果如果遇到S1[i] != S2[j] ，且c[i-1][j] = c[i][j-1] 这种存在分支的情况，选择另一个方向，会得到另一个结果。

即LCS ={3,5,7,7,8}。

在倒推时，如果s1[i] == s2[j] 就跳转到c[i - 1][j - 1],如果s1[i] != s1[j], 就向前找或向上找（只能一个方向）

PS：在代码中和解说中代码细节有所不同，在解说图中s从下标1开始，在代码中从下标0开始。

---------------------

作者：someone_and_anyone

来源：CSDN

原文：https://blog.csdn.net/someone_and_anyone/article/details/81044153