洛谷P3625 - [APIO2009]采油区域

Portal

Description

给出一个\(n\times m(n,m\leq1500)\)的矩阵，从中选出\(3\)个互不相交的\(k\times k\)方阵，使得被选出的数的和最大。

Solution

奇怪做法...



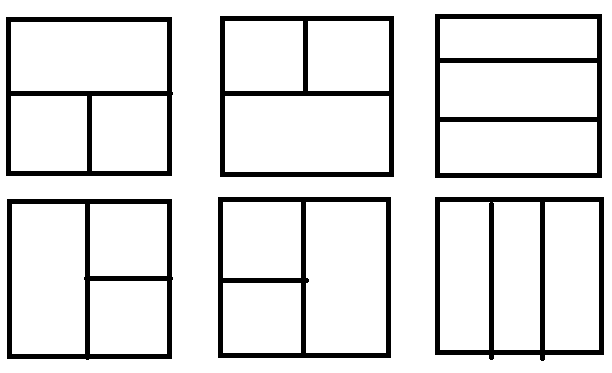
三个矩形分别在三个部分中，把矩形划分成三部分只有这六种。首先搞出\(s[i][j]\)表示以\((i,j)\)为右下角的\(k\times k\)方阵的和，然后搞出\(f_1[i][j]\)表示\((1,1)-(i,j)\)中\(s\)的最大值，\(f_2[i][j]\)表示\((1,m)-(i,j)\)中\(s\)的最大值，\(f_3[i][j]\)表示\((n,m)-(i,j)\)中\(s\)的最大值，\(f_4[i][j]\)表示\((n,1)-(i,j)\)中\(s\)的最大值。枚举横竖划分在哪就可以解决四种。

平行的那两种搞出行/列最大值然后瞎搞即可。

时间复杂度\(O(nm)\)。

Code

//[APIO2009]Oil
#include <cstdio>
const int N=2000;
inline int max(int x,int y) {return x>y?x:y;}
int n,m,k,a[N][N];
int pre[N][N],s[N][N],f1[N][N],f2[N][N],f3[N][N],f4[N][N],row[N],col[N];
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    int ans;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
    for(int i=k;i<=n;i++)
        for(int j=k;j<=m;j++)
            s[i][j]=pre[i][j]-pre[i-k][j]-pre[i][j-k]+pre[i-k][j-k];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            f1[i][j]=max(s[i][j],max(f1[i-1][j],f1[i][j-1]));
    for(int i=1;i<=n;i++)
        for(int j=m;j>=1;j--)
            f2[i][j]=max(s[i][j+k-1],max(f2[i-1][j],f2[i][j+1]));
    for(int i=n;i>=1;i--)
        for(int j=m;j>=1;j--)
            f3[i][j]=max(s[i+k-1][j+k-1],max(f3[i+1][j],f3[i][j+1]));
    for(int i=n;i>=1;i--)
        for(int j=1;j<=m;j++)
            f4[i][j]=max(s[i+k-1][j],max(f4[i+1][j],f4[i][j-1]));
    for(int i=k;i<=n-k;i++)
        for(int j=k;j<=m-k;j++)
        {
            ans=max(ans,f1[i][j]+f2[i][j+1]+f3[i+1][1]);    //┴
            ans=max(ans,f2[i][j+1]+f3[i+1][j+1]+f4[1][j]);  //├
            ans=max(ans,f3[i+1][j+1]+f4[i+1][j]+f1[i][m]);  //┬
            ans=max(ans,f4[i+1][j]+f1[i][j]+f2[n][j+1]);    //┤
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            row[i]=max(row[i],s[i][j]),col[j]=max(col[j],s[i][j]);
    for(int i=k;i<=n-k-k;i++)
        for(int j=i+k,mid=row[j];j<=n-k;j++,mid=max(mid,row[j]))
            ans=max(ans,f1[i][m]+mid+f3[j+1][1]);
    for(int i=k;i<=n-k-k;i++)
        for(int j=i+k,mid=col[j];j<=n-k;j++,mid=max(mid,col[j]))
            ans=max(ans,f1[n][i]+mid+f3[1][j+1]);
    printf("%d\n",ans);
    return 0;
}

P.S.

写的我好难受...