UVA10129：Play on Words（欧拉回路）

Some of the secret doors contain a very interesting word puzzle. The team of archaeologists has to solve it to open that doors. Because there is no other way to open the doors, the puzzle is very important for us.

一些密门会包含有趣的文字谜，考古学家小队为了开门不得不解决它。别无他法，谜题对我们很重要。

There is a large number of magnetic plates on every door. Every plate has one word written on it. The plates must be arranged into a sequence in such a way that every word begins with the same letter as the previous word ends. For example, the word ‘acm’ can be followed by the word ‘motorola’. Your task is to write a computer program that will read the list of words and determine whether it is possible to arrange all of the plates in a sequence (according to the given rule) and consequently to open the door.

每个门上会有大量磁盘且每个磁盘会有一个单词刻于其上。磁盘必须以此为序进行安排：每个单词的首字母必须与上一个单词的尾字母相同。例如“acm”后面可接“motorola”。你的任务就是写个程序来读入这些单词并判断是否有可能把它们安排明白以开门。

Input
The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing a single integer number N that indicates the number of plates (1 ≤ N ≤ 100000). Then exactly N lines follow, each containing a single word. Each word contains at least two and at most 1000 lowercase characters, that means only letters ‘a’ through ‘z’ will appear in the word. The same word may appear several times in the list.

输入：第一行输入T代表会有T组测试数据。接下来每组会以一个整数N开始，暗示了会有N个磁盘（1 ≤ N ≤ 10万）。接下来的N行每行一个单词，单词包含2~1000个小写字母。相同的单词是可以多次出现的。

Output
Your program has to determine whether it is possible to arrange all the plates in a sequence such that the first letter of each word is equal to the last letter of the previous word. All the plates from the list must be used, each exactly once. The words mentioned several times must be used that number of times. If there exists such an ordering of plates, your program should print the sentence ‘Ordering is possible.’. Otherwise, output the sentence ‘The door cannot be opened.’

输出：对于每组数据，所有的单词必须都要用上，某单词出现了几次就要用几次。如果可以穿成一串，就是存在一种可能的顺序，打印语句“Ordering is possible.”；否则打印“The door cannot be opened.”

Sample Input
3

2

acm

ibm

3

acm

malform

mouse

2

ok

ok

Sample Output
The door cannot be opened.

Ordering is possible.

The door cannot be opened.

介绍：欧拉回路

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。

如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。

 

欧拉回路是数学家欧拉在研究著名的德国哥尼斯堡(Koenigsberg)七桥问题时发现的。如图所示，流经哥尼斯堡的普雷格尔河（Pregel）中有两个岛，两个岛与两岸共4处陆地通过7座桥彼此相联。7桥问题就是：是否存在一条路线，可以不重复地走遍7座桥。

欧拉大佬把七桥问题改写成了图。则问题变成了：能否从无向图中的一个结点出发走出一条道路，每条边恰好经过一次。这样的路线就叫欧拉路径，也可以形象地称为“一笔画”。

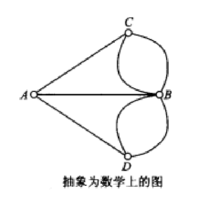
不难发现，在欧拉道路中，进和出是对应的——除了起点和终点外，其他点的进出次数应该相等。换句话说，其他点的度数（degree）应该是偶数（我们把进入称为入度，出去称为出度）。在七桥问题中，所有4个点的度数均是奇数（这样的点称为奇点），因此不可能存在欧拉道路。

在此不加证明地给出欧拉道路和回路的存在条件，请结合生活实际验证：

那么介绍到这里，应该就可以自己动手编写这道欧拉路径的裸题了，先判断度数，再判断连通性即可。建议自己实现，有问题再参考别人程序。

此处给出两种判断连通性的代码，由于DFS和并查集都是基础算法，暂时不做冗余介绍~

DFS：

 #include <bits/stdc++.h>
 using namespace std;

 string str;
 int test, n;
 int ru[], chu[];//入度和出度
 bool table[][], vis[];

 bool dfs(int cur)
 {
     vis[cur] = true;
     for (int i = ; i < ; i++)
         if (cur != i && table[cur][i] && !vis[i])
             dfs(i);
 }

 bool ok()
 {
     for (int i = ; i < ; i++)
         if (vis[i])
             n--;
     return n == ;
 }

 int main()
 {
     cin >> test;
     while (test--)
     {
         //初始化
         memset(table, false, sizeof(table));
         memset(vis, false, sizeof(vis));
         memset(ru, , sizeof(ru));
         memset(chu, , sizeof(chu));
         //输入
         cin >> n;
         for (int i = ; i <= n; i++)
         {
             cin >> str;
             int x = str[] - 'a', y = str[str.length()-] - 'a';
             table[x][y] = table[y][x] = true;//邻接矩阵制作无向图
             chu[x]++;
             ru[y]++;
         }
         //计算度数是否符合条件
         int a = , b = , c = -, d = ;
         n = ;
         for (int i = ; i < ; i++)
         {
             if (ru[i] == chu[i])
             {
                 a++;
                 if (!ru[i])//用来判定最后出现了几个字母
                     n--;
             }
             else if (ru[i] == chu[i]-)    b++, c = i;
             else if (ru[i] == chu[i]+)    d++;
         }

         if ((b ==  && d ==  && a == ) || a == )
         {
             if (c == -)//即a==26时
                 for (int i = ; i < ; i++)
                     if (chu[i])
                     {
                         c = i;
                         break;
                     }
             dfs(c);
             if (ok())
             {
                 puts("Ordering is possible.");
                 continue;
             }
         }
         puts("The door cannot be opened.");
     }
     return ;
 }

并查集：

 #include <cstdio>
 #include <cstring>
 #include <vector>

 int n;
 int f[], degree[];
 char str[];
 bool vis[];//标记某字母是否出现过
 std::vector <int> v;//储存奇点

 void init()
 {
     memset(degree, , sizeof(degree));
     memset(vis, false, sizeof(vis));
     v.clear();
     for (int i = ; i < ; i++)    f[i] = i;//并查集的预处理
 }

 int getf(int v)
 {
     return v == f[v] ? v : f[v] = getf(f[v]);
 }

 void input()
 {
     scanf("%d", &n);
     while (n--)
     {
         scanf("%s", str);
         int x = str[] - 'a', y = str[strlen(str)-] - 'a';

         vis[x] = vis[y] = true;
         degree[x]++, degree[y]--;
         int t = getf(x), p = getf(y);
         if (t != p)
             f[p] = t;
     }
 }

 bool cal()
 {
     int cc = ;//有多少个连通块
     for (int i = ; i < ; ++i)
     {
         if (degree[i] != )
             v.push_back(degree[i]);
         if (vis[i] && f[i] == i)
             cc++;
     }
     return cc ==  && (v.empty() || (v.size() ==  && (v[] ==  || v[] == )));
 }

 int main()
 {
     int test;
     scanf("%d", &test);
     while (test--)
     {
         init();//初始化
         input();//输入 + 并查集处理
         printf("%s\n", cal() ? "Ordering is possible." : "The door cannot be opened.");
     }
 }