Paxos算法学习
早在1990年,Leslie Lamport(即 LaTeX 中的"La",微软研究院科学家,获得2013年图灵奖)向ACM Transactions on Computer Systems (TOCS)提交了关于Paxos算法的论文The Part-Time Parliament。几位审阅人表示,虽然论文没什么特别的用处,但还是有点意思,只是要把Paxos相关的故事背景全部删掉。Leslie Lamport心高气傲,觉得审阅人没有丝毫的幽默感,于是撤回文章不再发表。直到1998年,用户开始支持Paxos,Leslie Lamport重新发表文章,但相比1990年的版本,文章没有太大的修改,所以还是不好理解。于是在2001年,为了通俗性,Leslie Lamport简化文章发表了Paxos Made Simple,这次文中没有一个公式。
三篇论文
The Part-Time Parliament
中间的一篇据说是内容差不多,小弟不才来读一下这三篇文章哈,求不被虐哭。
Paxos Made Simple
第一篇 The Part-Time Parliament
The Part-Time Parliament
(part-time:兼职,兼任的意思;parliament:议会,国会)
(看这个题目完全懵逼,不知道是啥意思)

(一共33个page,还好)
兼职议会
Leslie Lamport(张国荣是不是叫Leslie啊)
这篇文章出现在ACM Transactions on Computer System 16,2(1998年5月),133-169页。在2000年8月29日对本文做了少量修正。
(这个ACM Transactions on Computer System期刊在百度上搜索也没人人来评价这个期刊)
兼职议会
LESLIE LAMPORT
Digital Equipment Corporation(数字设备公司)
近期在Paxos岛上的考古学发现揭示了议会仍旧可以在它的兼职立法者有巡游倾向的时候起作用。即使经常受到来自议院的突袭和消息传递者的健忘困扰,立法者仍旧可以维持议会记录拷贝的一致性。Paxon议会协议提供了一个新的方法来实现状态机,从而完成对分布式系统的设计。
分类和学科描述:C2.4 [计算机通信网络]:分布式系统——网络操作系统;D4.5 [操作系统]:可靠性——容错;J.1 [行政数据处理]:政府
一般术语:设计,可靠性
额外关键词和词组:状态机,三阶段提交,投票
这篇投稿是最近才从TOCS编辑部的文件柜中发现的。虽然它有一定的年纪了,主编辑认为这篇文章有发表的价值。由于作者正在希腊的小岛上做相关领域的工作而且联系不到,因此我被委托来准备它的发表。
作者似乎是一个对计算机科学有着短暂兴趣的历史学家。(真是佩服些人。)这真是不幸;即使他所描述的晦涩的古Paxon文明对于绝大多数的计算机科学家而言并不会引起太大的兴趣,但是他的立法系统对于在一个异步环境中如何实现一个分布式的计算机系统是一个绝妙的模型。确实,某些Paxons对他们的协议所做的改进似乎在系统文献中是未知的。
作者确实在第四部分简单地讨论了下Paxon议会和分布式计算之间的关联。计算机科学家很可能想要先读这一部分。即使在那之前,他们可能想要先读一下Lampson是如何对计算机科学家解释这个算法的。这个算法同样被De Prisco等人更加正式的描述。我在第四部分的末尾对古老的协议和近期的工作的关联也做了进一步的评论。
Keith Marzullo
加尼福利亚大学,圣迭戈
1 问题
1.1 Paxos岛
在本千年(作者的论文是1998年)的早期,Paxos的爱琴岛是一个繁荣的商业中心。财富导致了政治的复杂,Paxons用议会形式的政府来代替古老的政教合一。但是贸易要比公民的义务先行,而且在Paxos没人愿意为Parliament献出生命。Paxon Parliament必须在立法者不断地在议会的议院进进出出的时候起作用。
用兼职的议会来进行行政管理的问题和如今分布系统的容错有着非常显著的对应关系,其中立法者对应于进程而议院则对应于失效。Paxons的解决方法也许引起计算机科学家的某些兴趣。在这里我描述了Paxos Parliament协议的简单历史,然后更加简短地讨论了一下它和分布式系统之间的关联。
Paxon文明因为外族入侵而被摧毁,考古学家近来已经开始发掘它的历史。因此我们对于Paxon Parliament的了解也是残缺不全的。虽然了解基本的协议,但是很多的细节仍是不得而知的。
1.2 需求
Parliament的主要任务是确定当地的法律,而法律则是由它通过的一系列法令来定义的。现代的议会采用秘书来记录它的议案,但是在Paxos没人愿意在这个会话中一直作为秘书留在议院中。而是每个Paxon的立法者维护一个记录了已经通过的带序号的法案的总账。比如,立法者 的总账有如下条目:
的总账有如下条目:
155: The olive tax is 3 drachmas per ton
如果她认为议会通过的第155条法令将橄榄的税定为3德拉马克每吨。总账用不可磨灭的墨水书写,并且它们的条目不能被改变。
对于议会协议的第一个需求就是总账的一致性,这意味着任何两本总账都不可以有矛盾的信息。如果立法者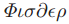 在他的总账中有如下条目:
在他的总账中有如下条目:
132: Lamps must use only olive oil
那么其他的立法者的总账中不能有和132法令不同的条目。然而其他的立法者如果还不知道法令已经通过了,那么在他的总账中可能没有132法令。
总账的提供的一致性是不足的,因为这种一致性可以通过将所有的总账都置空而很容易的达到。因此有一些其他的需求来保证法令最终通过并记录在总账中。在现代的议会中,法令的通可以被立法者的反对而阻碍。这个在Paxos并不存在,因为Paxos里每个人都相互信任。Paxon的立法者愿意通过任何提出的法令。然而,他们的巡回倾向可能会带来问题。
如果一组立法者通过这个法令:
37: Painting on temple walls is forbidden
并且然后离开并赶去赴宴,于是另一组立法者进入议院并且对于所发生的一无所知,然后通过了如下矛盾的法令:
37: Freedom of artistic expression is guaranteed
这个过程并不能得到保证,除非立法者在议院中待的时间足够长。因为Paxon的立法者都不想缩短它们外部活动的时间,因此不可能保证每条法令都会通过。然而,立法者在议院的时候他们愿意保证这个,他们和他们的助手会及时地对所有的议会事务进行响应。这种保证允许Paxons来设计一个满足如下过程条件的议会协议。
如果大多数的立法者都在议院中并且没有人在足够长的时间内进入或者离开议院,那么一个立法者提出的任何法令都可以获得通过,并且每条通过的法令会出现在议院的每个立法者的总账中。
1.3 假设
议会协议的要求仅在提供立法者足够多的资源的时候才能达到。每个立法者要有一个牢靠的总账来记录法令,一支笔以及得到不可磨灭的墨水。立法者也许会在离开议院时忘记它们正在做的事情,因此它们会在总账的背面做笔记来提醒它们议会任务的重要性。法令列表中的某个条目永远不会被改变,但是笔记可以被划掉。获得过程条件需要立法者能够度量逝去的时间,因此他们都有简单的滴漏计时器。
立法者们随时都会带着他们的总账,并且随时可以读取总账中的法令和未被划去的笔记。总账由精细的羊皮纸制成并且只记录那些重要的笔记。立法者会在纸上写下其他的笔记,但是当离开议院的时候这些纸可能会也可能不会丢失。
议院的音响设备很差,因此要发表演讲是不可能的。立法者仅仅依靠信使传递消息并且被提供了一笔资金来来雇佣它们所需的足够多的信使。信使足够可靠不会对携带的信息断章取义,但是他可能会忘记他已经发送了一条消息,并且继续发送这条消息。就像他们所服务的那些立法者一样,信使仅仅会贡献他们一部分的时间给议会任务。一个信使可能会离开议院做一些其他的事情——也许是进行6个月的远航——在发送消息之前。信使也可能永远离开议会,这种情况下消息将永远不会被发送。
虽然立法者和信使可以在任何时间进出议院,但是当身处议院中的时候他们会对议会的事情进行投票。当他们继续留在议会中的时候,信使会及时的发送消息立法者也会及时地响应它们收到的消息。
Paxos官方的记录声称立法者和信使都是严格诚实并严格遵循议会协议。大多数的学者认为这只是一种宣传,为了把Paxos描绘得在道德上超过他的东部邻居。虽然不信任的情况很少,但是无疑确实会发生。然而,由于在官方的文件中从未提到过,我们也不知道议会是如何处理不诚实的立法者和信使的。在3.3.5节讨论了有哪些被发现的证据。
2 单法令的主教会议
Paxon议会从早期仪式每19年召开一次来选择单条象征性法令的牧师主教会议演化而来。在很多个世纪中,主教会通过所有牧师都必须在场的常规过程来挑选法令。但是随着商业的繁荣,牧师主键游离于议院,但是主教会议仍在进行中。最后,老的协议失效了,并且主教会议因为没有选出法令而结束了。为了防止这种神学上的灾难的重复,Paxon的地区领导人要求数学家想出一个协议来选择主教会议的法令。这个协议的要求和假设和之后的Parliament基本上是一样的,除了在包含一系列的法令上之外,一本总账上最多只有一条法令。这里描述主教协议的结果;在第三部分会描述Parliament协议。
数学家们用一系列的步骤导出了主教会议协议。首先,它们证明了一个满足某种约束的协议可以保证一致性并允许进展下去。一个初步的协议就直接冲这些约束中导出来了。初步协议的严格版本提供了保证一致性的基本协议,但并没有进步。满足一致性和进展要求的完整版主教协议可以通过限定基本协议而得到。在2.1节描述了数学结果,并且在2.2-2.4节非正式地对协议进行了描述。更加正式的描述和对基本协议的修正证明在附录中有。
2.1 数学结果
主教会议的法令通过一系列带编号的选票选出来,其中每个选票会投在单条法令上。在每个选票中,一个牧师对于每条法令只有投票和不投票的权力。和一个选票关联的是被称为法定人数的牧师集合。一个选票仅且只在每个在法定人数中的牧师都赞成那条法令才会生效。正式地,选票B包含了如下4个部分(除非特别声明,set被认为是有限集。)

dec:正在被投票的法令
qrm:牧师的非空集合(投票的法定人数)
vot:牧师的集合(对这条法令进行投票的所有的牧师)
bal:投票的号码
一个投票B被认为是成功的当且仅当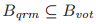 ,因此一个成功的投票是每个在法定人数中的成员都投票了。
,因此一个成功的投票是每个在法定人数中的成员都投票了。
投票号码是从一个无界的有序数的集合中选出来的。如果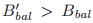 ,那么投票
,那么投票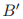 要比投票
要比投票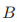 晚。然而这对于进行的投票在顺序上并没有什么意义;一个较晚的投票实际上很有可能要比早的那个先发生。
晚。然而这对于进行的投票在顺序上并没有什么意义;一个较晚的投票实际上很有可能要比早的那个先发生。
Paxon的数学家对于投票的集合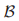 定义了三种条件,并且表明了如果投票的集合已经发生并且满足了下面的条件那么一致性可以得到保证以及进展是可能的。前两个条件很简单;它们可采用如下非正式的描述。
定义了三种条件,并且表明了如果投票的集合已经发生并且满足了下面的条件那么一致性可以得到保证以及进展是可能的。前两个条件很简单;它们可采用如下非正式的描述。
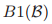 每个
每个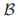 中的投票有唯一的投票号。
中的投票有唯一的投票号。
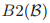
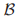 中任何两个投票的法定人中至少有一个共同的牧师。
中任何两个投票的法定人中至少有一个共同的牧师。
第三个条件要更加复杂一点。一个Paxon手稿中下面相当迷惑的陈述。
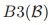 对于
对于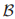 中的每个投票,如果任何一个
中的每个投票,如果任何一个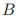 中的牧师在
中的牧师在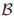 中的早一点的投票中投了票,那么
中的早一点的投票中投了票,那么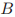 投票的法令等同于这些早期投票中的最近的一个的法令。对这些神秘文字的解释是在图1中描述的手稿帮助下进行的,采用了主教议会中包含了5个牧师A, B, Γ, ∆, 和 E的5个投票的集合
投票的法令等同于这些早期投票中的最近的一个的法令。对这些神秘文字的解释是在图1中描述的手稿帮助下进行的,采用了主教议会中包含了5个牧师A, B, Γ, ∆, 和 E的5个投票的集合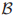 来描述了条件
来描述了条件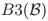 。集合
。集合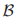 中包含了5个投票,对于每个投票投票人的集合是在名字在盒子中的法定人数的子集。例如投票13有一个法令α,一个包含了3个牧师的法定人数,以及两个投票者的集合。条件
中包含了5个投票,对于每个投票投票人的集合是在名字在盒子中的法定人数的子集。例如投票13有一个法令α,一个包含了3个牧师的法定人数,以及两个投票者的集合。条件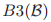 有如下形式:"对于
有如下形式:"对于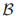 真的每个
真的每个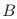 ...",其中"..."是在投票
...",其中"..."是在投票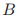 上的条件。对于图1中的5个投票的条件是如下的。
上的条件。对于图1中的5个投票的条件是如下的。

2. 投票号2是一个较早一点的投票,所以在这个投票的条件是平凡的为真。
5. 由于投票5中的4个法定成员没有一个在早一点的投票中投过票,因此在投票5上的条件也是平凡地为真。
14. 在投票14中唯一一个在早前的投票中投过的是 ,他在投票号2中已经投过票了,因此需要14法令必须和投票2的法令相同。
,他在投票号2中已经投过票了,因此需要14法令必须和投票2的法令相同。
27. (这是一个成功的投票。)在投票27中的法定成员是A, Γ, 和 ∆。牧师A并没有在早期的投票中投过票,唯一的早期投票中Γ在5号投票中投过票了,并且唯一的早期投票∆是在投票2中。在这两个投票中最近的一次是投票5,因此条件需要投票27和投票5的法令必须相同。
29. 投票29中的法定成员是B, Γ, 和 ∆。B早期投的唯一投票是14,牧师Γ在投票5和27中投过票了,并且∆在2和27中投过票了。四次投票中最近的一次是27,因此需要27和29号投票的法令是相同的。
接下来到了用数学来正式表示的地方了。呜呜呜
为了正式地陈述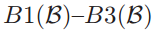 我们需要更多的记号。一次投票(vote)v被定义为包含了三个组成的对象:一个牧师
我们需要更多的记号。一次投票(vote)v被定义为包含了三个组成的对象:一个牧师 ,一个投票号
,一个投票号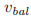 ,和一个法令
,和一个法令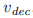 。它表示牧师
。它表示牧师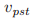 为法令
为法令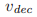 在投票号
在投票号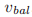 中投了票。Paxons同样定义了null投票为v,其中
中投了票。Paxons同样定义了null投票为v,其中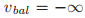 ,
,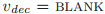 ,而且
,而且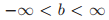 对于任意的投票号b,BLANK不是一个法令。对于任意的牧师p,定义了对于
对于任意的投票号b,BLANK不是一个法令。对于任意的牧师p,定义了对于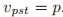 的唯一的空投票v为
的唯一的空投票v为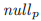 。
。
Paxon的数学家定义了所有投票的整个顺序,但是部分包含了定义的手稿已经遗失了。残留的碎片表明对于任意的投票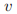 和
和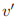 ,如果
,如果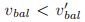 则
则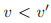 。但是当定义了
。但是当定义了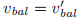 后就不知道了
后就不知道了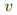 和
和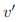 的相对顺序。
的相对顺序。
对于任意的选票集合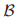 ,在
,在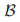 中的投票集合
中的投票集合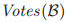 被定义为包含了所有的的投票v,使得对于某些
被定义为包含了所有的的投票v,使得对于某些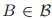 而言,
而言,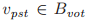 ,
,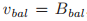 并且
并且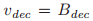 。如果p是一个牧师,b是一个选票号或者是
。如果p是一个牧师,b是一个选票号或者是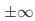 ,那么
,那么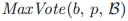 就被定义为由p投出的
就被定义为由p投出的 或者是如果没有这个投票
或者是如果没有这个投票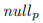 在
在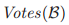 中最大的投票。由于
中最大的投票。由于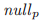 要比由p投出的任意实际的票要小,这意味着
要比由p投出的任意实际的票要小,这意味着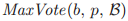 是在如下集合中最大的的投票
是在如下集合中最大的的投票
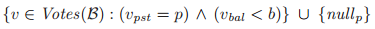
对于任意的非空牧师集合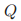 ,
,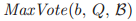 被定义为等于所有的在
被定义为等于所有的在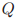 中的牧师p所有
中的牧师p所有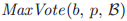 中最大的一个。
中最大的一个。
那么条件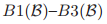 可以用如下方式来正式的表示了:
可以用如下方式来正式的表示了:
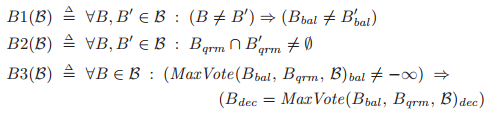
虽然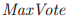 的定义依赖于投票的顺序,
的定义依赖于投票的顺序,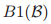 意味着
意味着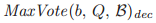 和每个选票号的排序是无关的。
和每个选票号的排序是无关的。
为了表明这些条件可以导出一致性,Paxons首先证明了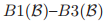 意味着如果在选票
意味着如果在选票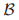 中选票
中选票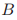 成功了,那么任何之后在
成功了,那么任何之后在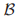 中的选票的法令都和
中的选票的法令都和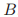 中的一样。
中的一样。
引理 如果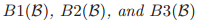 成立,那么
成立,那么
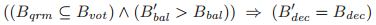
对于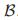 中任意的
中任意的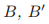 也都成立。
也都成立。
引理的证明
先不看证明了,把问题弄明白再看。
2.2 初始协议
Paxons从为了使条件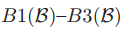 仍然为真的需求推导了preliminary protocol,其中
仍然为真的需求推导了preliminary protocol,其中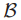 是已经进行了或者正在进行的所有的ballot的集合。协议的定义指明了集合
是已经进行了或者正在进行的所有的ballot的集合。协议的定义指明了集合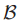 是如何改变的,但是集合从来没有被明确的计算出来。Paxons用一个只有上帝知道的对象来指代
是如何改变的,但是集合从来没有被明确的计算出来。Paxons用一个只有上帝知道的对象来指代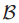 ,因为它对于任何凡人来说都是未知的。
,因为它对于任何凡人来说都是未知的。
每个ballot由一个牧师来进行初始化,这个牧师会选定这个ballot的号码,法令以及投票的群体。在选出来的投票群体中的每个牧师会在这场ballot中决定是否投票。用来决定开始的那个牧师如果选定ballot的号码以及法令还有投票群体,以及一个牧师在一场ballot中如何决定是否投票的规则都可以通过需要维持 来直接推导。
来直接推导。
为了维持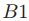 ,每场ballot必须有一个唯一的号码。通过记起来(用他在总账中的笔记)他之前已经初始化过的ballots,一个牧师可以很容易的避免用相同的号码来初始化两个不同的ballots。为了阻止两个不同的牧师用相同的号码来初始化不同的ballots,可能的ballot号会在牧师之间进行分区。如果仍旧不知道这个过程是如何完成的,一个显而易见的方法是让ballot的号码成为包含一个整数和牧师的一对,使用字典序,其中:
,每场ballot必须有一个唯一的号码。通过记起来(用他在总账中的笔记)他之前已经初始化过的ballots,一个牧师可以很容易的避免用相同的号码来初始化两个不同的ballots。为了阻止两个不同的牧师用相同的号码来初始化不同的ballots,可能的ballot号会在牧师之间进行分区。如果仍旧不知道这个过程是如何完成的,一个显而易见的方法是让ballot的号码成为包含一个整数和牧师的一对,使用字典序,其中:
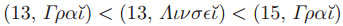
由于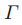 在Paxon的字母表中是在
在Paxon的字母表中是在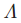 的前面。在任何例子中,每个牧师对于他所使用的任何无界的ballot数的集合是已知的。
的前面。在任何例子中,每个牧师对于他所使用的任何无界的ballot数的集合是已知的。
为了维持B2,一个ballot的quorum如果选择了包含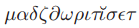 这些牧师。最开始,
这些牧师。最开始, 只是简单的大多数。之后的观察中会发现,更多的牧师的quorum的移动性会更差并且要比牧师少的quorum在Chamber中停留的时间更长,因此
只是简单的大多数。之后的观察中会发现,更多的牧师的quorum的移动性会更差并且要比牧师少的quorum在Chamber中停留的时间更长,因此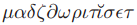 被拿来当做认为那些权重要比一半的牧师的权重更多的集合,而不是简单地多数的牧师。当一个瘦一点的牧师群体抱怨不公平的时候,实际的权重会用基于牧师到场记录的符号权重来代替。对于
被拿来当做认为那些权重要比一半的牧师的权重更多的集合,而不是简单地多数的牧师。当一个瘦一点的牧师群体抱怨不公平的时候,实际的权重会用基于牧师到场记录的符号权重来代替。对于 的主要需求是任意的两个包含了
的主要需求是任意的两个包含了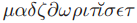 牧师的集合至少有一个共同的牧师。为了维持
牧师的集合至少有一个共同的牧师。为了维持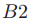 的条件,一个牧师会为ballot B选择
的条件,一个牧师会为ballot B选择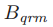 为大多数的集合。
为大多数的集合。
条件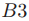 需要的是如果
需要的是如果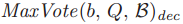 如果不等于BLANK,那么一个有着号码为b的投票群体为Q的ballot的法令必须为
如果不等于BLANK,那么一个有着号码为b的投票群体为Q的ballot的法令必须为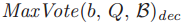 。如果
。如果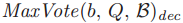 为BLANK,那么这个ballot可以是任何法令。为了维持
为BLANK,那么这个ballot可以是任何法令。为了维持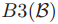 ,在用ballot号码b以及quorum Q初始化一个新的ballot之前,一个牧师必须找到
,在用ballot号码b以及quorum Q初始化一个新的ballot之前,一个牧师必须找到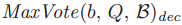 。为了完成这件事情,牧师p必须为Q中的每个牧师q找到
。为了完成这件事情,牧师p必须为Q中的每个牧师q找到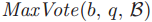 。
。
回想一下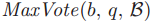 是在由q所投的所有投票中比投票号b要小的最大的投票号所对应的投票,或者是
是在由q所投的所有投票中比投票号b要小的最大的投票号所对应的投票,或者是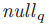 ,如果q并没有在任何小于b的ballot中投过票。牧师可以通过信息交换来获取牧师q的
,如果q并没有在任何小于b的ballot中投过票。牧师可以通过信息交换来获取牧师q的 。因此,前面在由p来通过协议的前面两个步骤初始化单个ballot的是:
。因此,前面在由p来通过协议的前面两个步骤初始化单个ballot的是:
(1)牧师p选择一个新的ballot号码并且向其他集合中的牧师发送NextBallot(b)。
(2)一个牧师q通过发送LastVote(b, v)信息响应对于NextBallot(b)响应发给p,其中v是q所作出的ballot号小于b的最大投票号码,或者是null vote如果q并没有在小于投票号b的投票中投过票。
牧师q必须使用它的总账背面的笔记来提醒自己它在之前投过了哪些票。
当q发送LastVote(b, v)信息的时候,v等于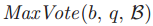 。但是投票集合
。但是投票集合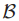 会随着新的投票创建以及投票进行而发生改变。由于牧师在选择法令来使得
会随着新的投票创建以及投票进行而发生改变。由于牧师在选择法令来使得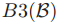 投票v作为
投票v作为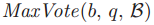 ,但需要保证在q发送了LastVote(b, v)信息之后,
,但需要保证在q发送了LastVote(b, v)信息之后,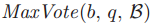 不会改变。为了阻止
不会改变。为了阻止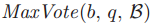 的改变,q必须对于
的改变,q必须对于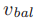 和b之间的ballot号码的投票不能进行新的投票了。(为了实现这个承诺,q必须在它的总账中记录必要的信息。)
和b之间的ballot号码的投票不能进行新的投票了。(为了实现这个承诺,q必须在它的总账中记录必要的信息。)
下面两个步骤在ballot协议(从步骤一中的牧师p开始)的是:
(3)在接收到了集合Q中大多数的牧师发出的LastVote(b, v)信息之后,牧师p会采用号码b以及群体Q和法令d来初始化一个新的ballot,其中d是选择的符合B3条件的法令,然后牧师会在它的总账后面记录下这个ballot,并且向Q中的每个牧师都发送一个BeginBallot(b, d)。
(4)一旦收到BeginBallot(b, d), 牧师q决定是否在b号ballot中进行投票。(他可能不会投票,如果这么做会和他所发送的LastVote(b', v')信息矛盾的话。)如果q决定对b号ballot投票,那么它会对p发送一个Voted(b, q)的信息并且在他的总账后面记录对ballot b的这次投票。
步骤三的执行被认为是将一个ballot B加入到了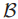 中,在ballot B中
中,在ballot B中 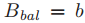 ,
,  (也就是还在还没有人在ballot中投过票),并且
(也就是还在还没有人在ballot中投过票),并且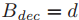 。在步骤4中,如果牧师q决定在ballot中投票,那么这个执行过程就相当于通过将q加入到在
。在步骤4中,如果牧师q决定在ballot中投票,那么这个执行过程就相当于通过将q加入到在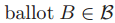 中的
中的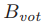 从而改变了ballot的集合
从而改变了ballot的集合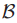 。
。
一个牧师可以选择不再步骤四中投票,即使投票不会和之前的诺言相违背。事实上,在上述的四个步骤中,所有的步骤都是可选的。例如,一个牧师q可以忽略NextBallot(b)信息,而只是执行步骤2.没能作出决策会阻止这个过程的继续,但是并不会造成任何的不一致问题,因为这样并不会是的条件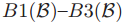 为假。由于不接受信息唯一的影响就是使得投票的行为进行不下去了,因此信息丢失也不会造成不一致性。因此这个协议可以保证即使在牧师离开了议院或者信息丢失的时候一致性也可以得到保证。
为假。由于不接受信息唯一的影响就是使得投票的行为进行不下去了,因此信息丢失也不会造成不一致性。因此这个协议可以保证即使在牧师离开了议院或者信息丢失的时候一致性也可以得到保证。
重复接受消息的拷贝会造成动作的重复执行。除了步骤3,其他步骤执行了2次也并没有什么影响。例如,在步骤四中发送了多次Voted(b, q)消息和发送一次的效果是一样的。通过使用在总账后面记录的条目可以防止步骤三的多次执行。因此,及时一个信息将相同的消息发送了多次之后一致性的条件也可以得到满足。
步骤(1)到(4)描述了用于对ballot进行初始化以及对它进行投票的完整协议。所有剩下要做的就是在一个法令完成选举之后决定ballotint的结果以及宣布。回想一下一个ballot成功当且仅当每个在quorum中的牧师都对法令进行投票了。一个成功的ballot的法令就是那个被Synod选出来的。协议剩下的步骤就是:
(5)如果p从Q(ballot号为b的法定投票人)的每个牧师q那里收到了Voted(b, q)消息,那么它会在它的总账撒花姑娘写下d(ballot的法令),并且向每个牧师发送一个成功的消息Success(d)。
(6)一旦接收到成功的消息,牧师就会把法令d记在它的总账上。
步骤(1)到(6)描述了单个的ballot是如何实施的。preliminary protocol允许任何牧师在任何时候初始化一个ballot。每一个步骤都维持条件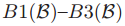 ,因此整个协议会维持这些条件。有一个一个牧师仅仅会在ballot的法令成功的时候才会把它记在总账中,定理1表明牧师的总账是一致的。这个协议并没有解决问题如何继续的问题。
,因此整个协议会维持这些条件。有一个一个牧师仅仅会在ballot的法令成功的时候才会把它记在总账中,定理1表明牧师的总账是一致的。这个协议并没有解决问题如何继续的问题。
在步骤3中,如果法令d是由条件B3决定的,那么有可能这条法令已经由某个牧师写到自己的总账中了。这个牧师不一定要在quorum Q中;他可能离开了议院。因此如果步骤三允许在选择法令d上有更大的自由时,一致性会得不到保证。
2.3 基本协议
在preliminary protocol中一个牧师必须记录:
(i)他所初始化的每个投票
(ii)他投的所有的票
(iii)他所发出的每个LastVote信息。
对于一个很忙的牧师来说要想记下来这么多东西是很困难的。Paxons因此对preliminary进行限制来获得更加实用的basic protocol,那么每个牧师只需要在他的总账后面维持一下信息就好了:
lastTried[p] 牧师p试图去初始化的最后一个ballot的号码,如果没有的话就是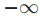 。
。
prevVote[p] 牧师p在他所投的票的ballot中号码最高的,如果牧师没有投过票的话就是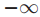 。
。
nextBal[p] p发送过的LastVote(b, v)消息的最大的b值,如果他从未发送者这种消息的话就是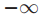 。
。
preliminary protocol 的步骤(1)-(6)描述了单个的ballot是如何由它的初始化人,牧师p,来实施的。preliminary protocol允许p并发地实施任何数量的ballots。在basic protocol中,他每次只会实施一个ballot——也就是ballot号为lastTried[p]的那个。在牧师p初始化了这个ballot之后,它会忽略那些属于他之前初始化的ballot的消息。牧师p在一张纸上记录所有的关于ballot号为lastTried[p]的过程。如果他遗失了这张纸,那么他就听停止进行这场ballot。
在preliminary protocol中,由牧师q发送的LastVote(b, v)消息代表着不会对任何ballot号在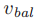 和b之间的ballot的投票的承诺。在basic protocol中,它代表了更强的承诺,即不会再小于b的ballot中进行新的投票。这个更强的承诺可能会阻止他在可以在preliminary protocol投票但是不能在basic protocol的步骤4中投票。然而由于preliminary protocol总是给牧师q不用投票的选择,basic protocol并不要求他去做任何preliminary protocol不允许做的事情。
和b之间的ballot的投票的承诺。在basic protocol中,它代表了更强的承诺,即不会再小于b的ballot中进行新的投票。这个更强的承诺可能会阻止他在可以在preliminary protocol投票但是不能在basic protocol的步骤4中投票。然而由于preliminary protocol总是给牧师q不用投票的选择,basic protocol并不要求他去做任何preliminary protocol不允许做的事情。
preliminary protocol中的步骤(1)~(6)变成了在basic protocol中实施的如下6个步骤。(所有p所选的执行ballot的信息,除了lastTried[p],prevVote[p]和nextBal[p]之外,也记录在一张纸上。)
(1)牧师p选择一个比lastTried[p]更大的ballot号b,并且将lastTried[p]设为b,然后将消息NextBallot(b)发送到牧师们的某个集合中。
(2)一旦从牧师p那里接收到了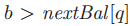 的NextBallot(b)的消息,牧师q会把nextBal[q]设置为b并且向p发送一个LastVote(b, v)的消息,其中v等于prevVote(q)。(如果
的NextBallot(b)的消息,牧师q会把nextBal[q]设置为b并且向p发送一个LastVote(b, v)的消息,其中v等于prevVote(q)。(如果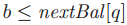 ,那么NextBallot(b)的消息会被忽略。)
,那么NextBallot(b)的消息会被忽略。)
(3)在某个大多数的集合Q中收到了每个牧师的LastVote(b, v)的消息,其中b=lastTried[p], 牧师p会用b, quorum Q以及法令d来初始化一个新的ballot,其中d从满足B3的条件中选。然后他会对Q中的每个牧师发送BeginBallot(b, d)的消息。
(4)一旦牧师q接收到了b=nextBal[q]的BeginBallot(b, d)的消息,牧师q会对ballot b进行投票,并且会prevVote[q]设置为这个投票,并且发送Voted(b, q)的消息给p。(如果b!=nextBal[q]的话,那么BeginBallot(b, d)的消息会被忽略。)
(5)如果p从Q(quorum for ballot number b)中的每个牧师哪里都收到了Voted(b, q)消息, 其中b=lastTried[p],那么它会将法令d(ballot的法令)写到他的总账中,并且对每个牧师都发送一个Success(d)的消息。
(6)一旦牧师收到了Success(d)的消息,那么他就会把法令d写到自己的总账中。
basic protocol是preliminary protocol的限制版本,意味着任何basic允许的动作在preliminary protocol中都是允许的。由于preliminary protocol满足一致性的条件,basic protocol也满足一致性的条件。就像preliminary protocol一样,basic protocol并不要求每个动作都必须执行,所以它也没有解决进行下去的问题。
从B1~B3对basic protocol的推导很容易发现可以满足一致性的条件。然而,有些相似的显而易见的古老智慧被证明是错误的,并且持怀疑态度的市民要求更加严格的证明。那么在附录后面有Paxon数学家对于协议满足一致性条件的证明。
2.4 完整的Synod Protocol
basic protocol可位置一致性的问题,但是它并不能确保进度因为它只是声明了一个牧师可能会做的事情;但是并没有要求他要做什么事情。完整的protocol包含了basic protocol中的相同的6个步骤。为了帮助达到进度,它包含了明显的额外条件,就是要求牧师尽可能快地执行协议的步骤2-6。然而,为了满足进度条件,需要某个牧师来完成步骤1,也就是初始化一个ballot。complete protocol的关键在于决定由哪个牧师来初始化一个ballot。
如果永远都不初始化一个ballot显然会阻止进度。然而,初始化了太多的ballot同样会阻碍进度。如果b是比其他任何ballot号都要大,那么在步骤2中牧师q接收到NextBallot(b)的消息可能会引发一个阻止他在步骤四中对任何之前初始化的ballot进行投票的承诺。因此,一个新的ballot的初始化会阻止任何之前初始化的ballot成功结束。如果新的ballot在之前的ballot可能成功结束之前继续用主键增长的ballot号进行初始化,那么进度将不会有任何改变。
要达到进度条件需要在直到一个新的ballot完成之前才能初始化一个新的ballot,但是那样的话它们就不能初始化得太频繁。为了发展complete protocoll,Paxons首先必须知道信使花多久的时间来传递消息以及牧师的响应。他们决定一个不离开议院的信使总是在4分钟之内发送一条消息,并且一个留在议院的牧师总是在7分钟之内执行完创建这个动作的事件。因此,如果p和q在某个事件使得p向q发送消息的时候都在议院中,并且q对p会进行响应,那么p会在22分钟内接收到响应如果信使都没有离开议院的情况下。(牧师p会在事件的7分钟内发送消息,q会在4分钟或则更多的时间后接收到消息,然后会用7分钟响应,并且在4分钟内由信使发送回复。)
假设仅仅只有一个牧师来初始化ballots,并且他在协议的步骤1中向每个牧师发送消息以此进行初始化。如果p在大多数的牧师都在议院中的时候初始化了一个ballot,那么他应该可以用22分钟来初始化ballot来执行步骤3,并在另外一个22分钟内执行步骤5.如果他不能在这些时间之内执行完步骤,那么在p初始化完成ballot之前某个牧师或者信使会离开议院,或者会有个ballot号码更大的ballot会被另外一个牧师初始化(在p称为唯一的那个初始化ballot的牧师之前)。为了处理后面的这种可能性,p必须了解任何比其他牧师的lastTried[p]大的ballot号码。这个可以通过扩展协议要求如果一个牧师q从p那里接受了一个NextBallot(b)或者BeginBallot(b, d)的消息而且b<nextBal[q]之后,然后他会向p发送一个包含nextBal[q]的消息。牧师p然后会用一个更大的ballot number来初始化一个新的ballot。
仍然假设p是那个唯一的初始化ballot的牧师,如果他需要初始化一个ballot当且仅当:
(i)他在之前的22分钟之内并没有执行step3或者step5,或者
(ii)他了解到有一个牧师初始化了一个号码更高的ballot。
如果议院的门是被p锁住了,而且大多数的牧师留在了里面,那么在99分钟之内一个法令会被通过并且记录在议院中所有牧师的总账中。(要花费22分钟对p开始一个新的ballot,22分钟的时候来了解另一个牧师初始化了一个更大号码的ballot,然后55分钟来完成步骤1-6获得一个成功的ballot。)因此,进度条件可以得到满足仅当一个唯一的牧师,不会离开议院,并且初始化ballots。
complete protocol因此包括了一个选择唯一的牧师的,也就是主席,来初始化ballots的步骤。在大多数形式的政府中,选择主席是一个困难的问题。但是,只有在大多数政府在任何时间只需要一个主席才会有这种困难。比如在美国,如果一部分人希望Bush当选,但是另一部分人又希望Dukakis当选,那么会造成混乱,因此它们其中的一个都可能会决定在法案上签字但是另一方会反对它。然而,在Paxon Synod,有多个主席仅仅会阻碍进度,而不会造成不一致的情况。为了使得complete protocol满足进度条件,那么选择主席的方法只要满足下列的presidential selection requirement就可以了:
如果没有人进入或者离开议院,那么在T分钟之后在议院中只有一个牧师会考虑让自己成为主席。
如果满足了主席选举要求的话,那么complete protocol就会有这样的属性:如果大多数的牧师都在议院中并且没有人在T+99分钟内进入或者离开议院,那么在这个周期结束之后在议院中的每个牧师都会在它们的总账中写下一条法令。
Paxons从身处议院中的所有牧师中选出名字在在字典序的最后一个的牧师作为主席,虽然我们并不知道这个是如何完成的。主席选举要求会在每T-11分钟内给其他牧师发送包含他的名字的消息而满足,并且一个牧师当且仅当他在T分钟之内没有收到比他名字排序更高的消息之后就认定自己是主席了。
complete Synod protocol可以通过basic protocol中要求牧师及时地完成步骤2-6,以及增加选出一个主席来初始化ballots的方法,以及主席在合适的时候初始化新的ballot从而得到满足。这个协议的很多细节都不得而知。我已经描述了一个用于选举主席的简单的方法以及决定主席在什么时候应该初始化一个新的ballot,但是它们无疑不是Paxos中所使用的。我给出的规则需要主席即使在一个法令在选择之后仍继续初始化ballots,因此需要确保刚进入议院的牧师要了解到选中的法令。这里显然有更好的方法来确保牧师了解到刚刚选出来的法令。同样,在选举主席的过程中,每个牧师可能向其他的牧师发送lastTried[p]的值,允许主席在第一次尝试的时候选择一个足够大的ballot number。
Paxons意识到任何protocol如果要达到进度条件的话就必须涉及到对时间的度量。给定了上述的选择主席以及初始化ballot的方法之后,协议很容易用精确的算法来描述,设置定时器以及在时间超时之后执行动作——假设有完美的精确地定时器。更进一步的分析表明这类protocol可以和一个进度范围的定时器一起工作。在Paxos有经验的玻璃鼓风机匠人可以毫无困难地制造一个合适的沙漏计时器。
考虑到Paxon数学家的复杂性,普遍认为必须找到一个最优的算法来满足主席选举需求。我们希望这中算法会在Paxos未来的发掘中被发现。
3 多法令议会
当议会成立之后,需要从Synod protocol中派生出来一个protocol来满足一致性以及进度需求。原始的parliamentary protocol的派生和属性在3.1和3.2节中描述。3.3节更进一步讨论了协议的发展。
3.1 协议
Paxon Parliament需要通过一些列带序号的法令,而不是仅仅只通过一条法令。就像在Synod protocol中那样会选出一个主席来。任何人想要通过一项法令需要先通知主席,然后主席会给该法令一条序号并且试图通过它。parliamentary protocol逻辑上使用分离的complete Synod protocol给每个法令的序号。然而,需要为这些实例都选出一个主席,并且主席只是完成一次协议的前两个步骤。
推导parliamentary protocol的关键是要观察到在Synod协议中,主席直到步骤3才会选择法令或者quorum。一个新当选的主席p可以为所有的的Synod实例的某些立法者发送一个单一的消息作为NextBallot(b)。(有无限个实例,并且每个实例都一个法令编号。)一个立法者q可以用作LastVote消息的单条消息为所有的Synod protocol的实例的步骤2。这条消息包含了有限的信息,由于q只能在有限个实例中投票。
当新的主席从大多数的集合中的每个那里都收到了响应,每个它准备为Synod protocol的每个实例执行步骤3.对于有限号码的实例(法令号码),在步骤3中法令的选择将会由B3来决定。主席会激励为试图通过这项法令的实例执行步骤3.然后,不管什么时候他收到了通过一个法令的请求,他会选一个他能够自由选择的最低号码的法令,然后为那个法令号执行步骤3(Synod protocol的实例)来试图通过这项法令。
对这个简单协议的修改得到了实际的Paxon Parliament's protocol。
——没有必要为一个已经知道的法令的结果来执行Synod protocol的步骤。因此,如果一个新选举的主席p有所有小于或者等于写在它的总账的法令n,那他会向Synod protocol所有的实例发送NextBallot(b, n)作为NextBallot(b)消息对那些法令号大于n的。在他对这些消息的响应中,立法者q会通通知所有法令编号大于n的已经在q的总账中出现了(除了发送通常的不在他的总账中的LastVote信息之外),并且它会要求p向他发送任何法令编号n或者小于那些不在他的总账的法令。
——假设法令125和法令126是在星期五下午的晚些时候引入的,法令126通过了并且写到了一到两个立法者的总账中,但是在任何事发生之前,立法者都回家过周末了。在假设在下个星期一, 被选举为新的主席并且了解到了法令126,但是她并不知道法令125,因为前一个主席和为它投票的所有的立法者仍然在议院外面。它会持有一个通过法令126的ballot,使得在总账中留下了间隙。将125号分配给一个新的法令会它比上周已经通过的法令126更早地出现在总账中。用这种方式通过无序的法令会造成疑惑——例如,如果市民提出了新的法令因为他知道法令126已经通过了。
被选举为新的主席并且了解到了法令126,但是她并不知道法令125,因为前一个主席和为它投票的所有的立法者仍然在议院外面。它会持有一个通过法令126的ballot,使得在总账中留下了间隙。将125号分配给一个新的法令会它比上周已经通过的法令126更早地出现在总账中。用这种方式通过无序的法令会造成疑惑——例如,如果市民提出了新的法令因为他知道法令126已经通过了。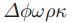 会通过如下法令:
会通过如下法令:
125: The ides of February is national olive day
一个传统的法令对于Paxos的任何人并没有绝对的意义。一般来说,一个新的主席将会通过"olive-day"法令来填补任何出现在总账中的空隙。
parliamentary protocol的一致性和进度可以立即从Synod protocol对应属性的推导而来。就我们所知的,Paxons从来不会因为写一个parliamentary protocol而困扰,因为很容易从Synod protocol中推导。
3.2 协议的属性
3.2.1 法令的排序 Balloting可以对很多不同的法令号码而并发的进行,只要通过不同的立法者来初始化ballots——每个在初始化ballot的时候都认为它是主席。我们不能精确的说明法令应该以何种顺序通过,尤其是在不知道主席是如何选出来的情况下。然而,对于法令的顺序有一个重要的属性需要被推导。
一个法令如果在步骤3中被主席从对应的实例中选出来被称之为提出。一个法令当他第一次被写入总账中被称之为通过。在一个主席可以提出一个新的法令之前,他必须了解到他么为这条法令投票的大多数成员中的每个成员。任何已经通过的法令必须被大多数中的至少一个立法者投票。因此,主席必须在初始化任何新的法令之前了解到所有之前已经通过的法令。主席可能不会使用重要的法令来填总账中的空隙——就是,用其他的法令而不是使用"olive-day"法令。主体不会提出无序的法令。一次,协议满足如下的法令有序属性。
如果法令A和B都是重要的并且A已经在B提出来之前通过了,那么A比B的法令号要低。
3.2.2 在关闭的门之后 即使我们不知道选出一个主席的细节,但是我们确实知道当主席选出来之后并且没有人进入或者离开议院的时候,Parliament是如何起作用的。一旦接收到了通过某个法令的请求——直接从市民那儿知道的或者是从另一个立法者那儿知道的——主席会分配一个法令并通过如下的信息交换来通过它。(以下的号码和Synod协议中的步骤对应。)
(3)主席向quorum中的每个立法者发送BeginBallot消息。
(4)在quorum中的每个立法者向主席发送一个Voted消息。
(5)主席向每个立法者发送Success消息。
这是3条信息延迟之和,而且大概是3N个消息,假设议会中的有N个立法者而且quorum中的立法者大约占N/2。而且,如果议会很忙的话,主席会将BeginBallot和前一个的Success信息一起发送,那么这样对于每个法令的话会有2N个消息发送。
3.3 进一步的发展
4 和计算机科学的关联
4.1 状态机方法
虽然Paxos的议会在很多世纪以前就被摧毁了,但是它的协议仍然十分有用。例如,考虑到一个简单的可能作为name server的分布式数据库系统。数据库的拷贝由多个服务器维护。一个客户端可以向任意的服务器中的名字发出读以及更新的请求。这里有两种读请求:一种是慢读(slow read),会返回当前赋给名字的值,还有一种就是快读,读的速度更快,但是也不会响应对数据库最近一次的变更。
在数据库系统和Paxon议会之间有着很明显的对应关系:


客户端对一个值进行修改的请求相当于去通过一条法令。一次慢读会涉及到通过一条法令,正如3.3.4节中所描述的那样。一次快读则是通过读取服务器当前版本数据库中的数据。Paxon议会协议提供了一个分布式的容错的数据库系统的实现。
这种实现的方法是一个分布式的数据库是状态机的实例,第一次在Lamport 1978中提到。在这种方法中,首先定义一个状态机,它包括了一系列的状态,一套命令,一套响应和一个分配响应/状态对的函数(这种对包括了响应以及状态)对于每个命令/状态对。直观上,状态机会通过产生响应来执行命令并且改变它的状态;命令和机器的当前状态决定了它的响应以及它的新值。对于分布式的数据库来说,一个状态机的状态就是一个数据库的状态。在图2中描述了指定响应和新状态的状态机命令以及函数。
系统的功能性是通过状态机来表达的,仅仅是一个从命令/状态到响应/状态的函数。同步和容错的问题是通过服务器来用一般的算法来执行一系列命令处理的。服务器会通过一套标准的已经证明为正确的分布式算法来获得状态机的指令。函数比分分布式的算法更容易设计并且获得正确的值。
第二篇 和第一篇差不多(省略)
第三篇
Paxos算法学习的更多相关文章
- paxos算法学习总结
核心思想 分布式系统架构下如何让整体尽快达成一致观点,也就是多个不同观点收敛到一个观点的过程. 难点 可能会发生少数节点故障,但绝不是大面积故障,不然系统也没法正常工作. 由于存在单点故障,因此不可能 ...
- paxos 算法原理学习
下面这篇关于paxos分布式一致性的原理,对入门来说比较生动有趣,可以加深下影响.特此博客中记录下. 讲述诸葛亮的反穿越 0.引子 一日,诸葛亮找到刘备,突然献上一曲<独角戏>,而后放声大 ...
- 模拟Paxos算法及其简单学习总结
一.导读 Paxos算法的流程本身不算很难,但是其推导过程和证明比较难懂.在Paxos Made Simple[1]中虽然也用了尽量简化的流程来解释该算法,但其实还是比较抽象,而且有一些细节问题没有交 ...
- Zookeeper学习之:paxos算法
paxos算法的重要性众所周知,它给如今的分布式一致性提供了迄今为止最好的解决方案.无论是Lamport自己的论文描述,还是网上的诸多资料,对paxos的描述都是及其简洁的,给人的感觉是paxos看似 ...
- 分布式系列文章——Paxos算法原理与推导
Paxos算法在分布式领域具有非常重要的地位.但是Paxos算法有两个比较明显的缺点:1.难以理解 2.工程实现更难. 网上有很多讲解Paxos算法的文章,但是质量参差不齐.看了很多关于Paxos的资 ...
- 分布式数据库中的Paxos 算法
分布式数据库中的Paxos 算法 http://baike.baidu.com/link?url=ChmfvtXRZQl7X1VmRU6ypsmZ4b4MbQX1pelw_VenRLnFpq7rMvY ...
- Paxos算法与Zookeeper分析
1 Paxos算法 1.1 基本定义 算法中的参与者主要分为三个角色,同时每个参与者又可兼领多个角色: ⑴proposer 提出提案,提案信息包括提案编号和提议的value; ⑵acceptor 收到 ...
- Ceph剖析:Paxos算法实现
作者:吴香伟 发表于 2014/10/8 版权声明:可以任意转载,转载时务必以超链接形式标明文章原始出处和作者信息以及版权声明 Recovery阶段 在Leader选举成功后,Leader和Peon都 ...
- Paxos算法细节详解(一)--通过现实世界描述算法
Paxos分析 最近研究paxos算法,看了许多相关的文章,概念还是很模糊,觉得还是没有掌握paxos算法的精髓,所以花了3天时间分析了libpaxos3的所有代码,此代码可以从https://bit ...
随机推荐
- POJ 2635 The Embarrassed Cryptographer (千进制,素数筛,同余定理)
The Embarrassed Cryptographer Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 15767 A ...
- 【Reship】use of tangible T4 template engine
1.first of all 之前在 “使用T4模板生成代码 – 初探” 文章简单的使用了T4模板的生成功能,但对于一个模板生成多个实例文件,如何实现这个方式呢?无意发现一个解决方案 “Multipl ...
- 自己写的页面加载进度条jquery插件
(function ($) { var progressId = "progress" + Math.round(Math.random() * 100) var progress ...
- luogu 1258 小车问题 小学奥数(?)
题目链接 题意 甲.乙两人同时从A地出发要尽快同时赶到B地.出发时A地有一辆小车,可是这辆小车除了驾驶员外只能带一人.已知甲.乙两人的步行速度一样,且小于车的速度.问:怎样利用小车才能使两人尽快同时到 ...
- getchar吸收回车
#include "stdio.h" int main() { int a; char b,c; scanf("%d",&a); c = getchar ...
- LeetCode OJ--Copy List with Random Pointer **
https://oj.leetcode.com/problems/copy-list-with-random-pointer/ 灵活的指针链表应用. 每个节点有两个指针next,random,对本链表 ...
- Android Studio查看其它APP的布局结构
概述 日常使用别家的APP过程中,会遇到一些比较好看的布局,这时候我们就想学习一下别人的布局结构,以便参考. (1)手机连接电脑.设置手机为USB调试模式 (2)运行Android Studio,打开 ...
- autofac 用法总结
autofac官网: http://autofaccn.readthedocs.io/en/latest/getting-started/index.html autofac作为一个热门ioc框架,还 ...
- NYOJ 27.水池数目-DFS求连通块
水池数目 时间限制:3000 ms | 内存限制:65535 KB 难度:4 描述 南阳理工学院校园里有一些小河和一些湖泊,现在,我们把它们通一看成水池,假设有一张我们学校的某处的地图,这个地 ...
- 牛客网 牛客小白月赛2 A.数字方阵-反魔方阵,梁邱构造法
天坑未补... 水一波博客,再不写博客就咸成鱼干了,只写题不写题解,过一段时间就忘了自己学过什么了. 最近重点就是把开学以来写的题补出来,没学的就滚去学会啊(= =),填一下坑... 从这篇博客开始, ...
