求斐波那契数列的第n项

问题描述：斐波那契数列是这样的一个数列，1，1，2，3，5，8，..，即前两项都是1，后面每一项都是其前面两项的和。

现在要你求出该数列的第n项。

分析：该问题是一个经典的数列问题，相信大家在很多语言的教科书上都碰到过这个练习题目。这里我给大家总结了三种经典解法，并对这三个方法进行了对比。

解法一：递归算法。很多教科书上都用这个题作为函数递归知识点讲解的例题，我们可以将每一个项的求法表达为这样一个式子：

f(n)=f(n-1)+f(n-2),f(1)=1,f(2)=1,可以看出，可以采用递归算法求解。

 解法二：循环求法。我们可以从第1项开始，一直求到第n项，即可，一个循环可以做到，时间复杂度为O(n).

解法三：矩阵链乘法。如果线性代数学的好的话，可以想出这样一种解法，

同样可以采用递归的算法求解，时间复杂度为O(logn).

三种解法对比：解法一编程最简单，但是效率最低，因为这种递归算法求解时，会重复求解子问题。如下图示：

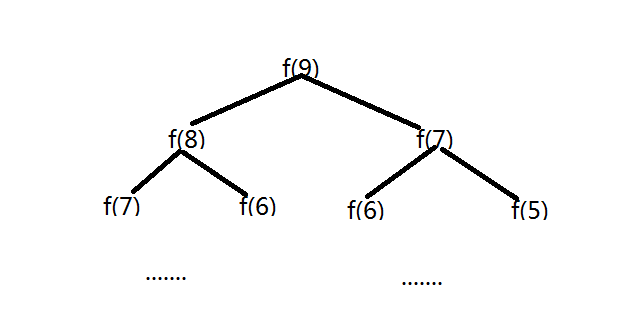
这样就看出来吧！另外如果n很大的话，递归的层数很大，会消耗系统大量的时间和资源。

解法二避免了重复求解子问题，线性时间即可求出，值得采用。

解法三效率最高，但是编程特别复杂，在有些情况下，很合适使用，但就本题目来说，推荐解法二。

针对上述三种解法，我给出了详细的Java代码，读者可以参考：

 import java.util.*;
 public class Main {
     public static int f1(int n){                     //方法一：递归算法，自底向上
         if(n<=2)return 1;                            //如果是求前两项，直接返回就可
         else return f1(n-1)+f1(n-2);
     }
     public static int f2(int n){                     //方法二：循环算法，自上而下
         if(n<=2)return 1;                            //如果是求前两项，直接返回就可
         int a1=1,a2=1,a3;
         for(int i=3;i<=n;i++)
             {
               a3=a1+a2;
               a1=a2;
               a2=a3;
             }
         return a2;
     }
     public static int[][] f3(int n){                 //方法三：矩阵链相乘算法，采用递归实现
         int a[][]={{1,1},{1,0}};                     //定义基矩阵
         int b[][];                                   //存储子方法的结果
         int c[][]=new int[2][2];                     //存储最后计算结果
         int d[][]=new int[2][2];                     //存储中间计算结果
         if((n)<=1)return  a;                         //如果次方小等于1直接返回
         else if((n) %2==1)
                  {b=f3((n-1)/2);

                  d[0][0]=b[0][0]*b[0][0]+b[0][1]*b[1][0];
                  d[0][1]=b[0][0]*b[0][1]+b[0][1]*b[1][1];
                  d[1][0]=b[1][0]*b[0][0]+b[1][1]*b[1][0];
                  d[1][1]=b[1][0]*b[0][1]+b[1][1]*b[1][1];

                  c[0][0]=d[0][0]*a[0][0]+d[0][1]*a[1][0];
                  c[0][1]=d[0][0]*a[0][1]+d[0][1]*a[1][1];
                  c[1][0]=d[1][0]*a[0][0]+d[1][1]*a[1][0];
                  c[1][1]=d[1][0]*a[0][1]+d[1][1]*a[1][1];

                 }
         else  {
              b=f3((n)/2);

              c[0][0]=b[0][0]*b[0][0]+b[0][1]*b[1][0];
              c[0][1]=b[0][0]*b[0][1]+b[0][1]*b[1][1];
              c[1][0]=b[1][0]*b[0][0]+b[1][1]*b[1][0];
              c[1][1]=b[1][0]*b[0][1]+b[1][1]*b[1][1];
         }
         return c;
     }
     public static void main(String[] args) {
         // TODO 自动生成的方法存根
         Scanner scan=new Scanner(System.in);
         int n=scan.nextInt();
         System.out.println("方法一："+f1(n));
         System.out.println("方法二："+f2(n));
         int a[][]=f3(n-1);                            //因为是要求矩阵{{1,0},{1,0}}的n-1次方
         System.out.println("方法三："+a[0][0]);

     }

 }

输出结果为：

10
方法一：55
方法二：55
方法三：55