Essentially No Barriers in Neural Network Energy Landscape

梗概
主要内容

Draxler F, Veschgini K, Salmhofer M, et al. Essentially No Barriers in Neural Network Energy Landscape[C]. international conference on machine learning, 2018: 1308-1317.

梗概

作者认为，神经网络中，假设$\theta_1, \theta_2$都是使得损失达到最小的参数，那么通过一些手段，可以找到一个路径(path)，沿着这条路径，其上的$\theta$也会使得损失很小，几乎与最小没什么区别.

并且作者给出了如何寻找，以及一种扩展方式.

可惜的是，这些都只是猜想，有许多事实支撑，但缺乏理论论证.

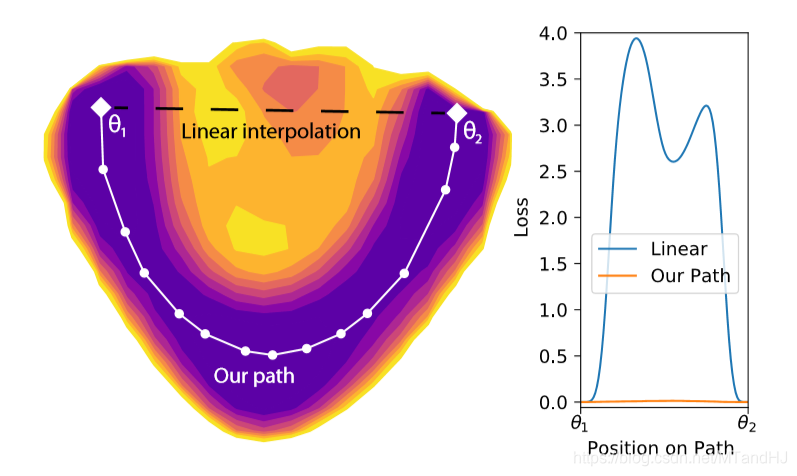
主要内容

path的定义

\[p(\theta_1, \theta_2)^*= \mathop{\mathrm{argmin}} \limits_{p \: from \: \theta_1 \: to \: \theta_2} \{\max_{\theta \in p} L(\theta)\}.
\]

可以说，这个定义非常之简单粗暴了.

需要一提的，作者是$\theta \in p(\theta_1, \theta_2)^*$中使得$L(\theta)$到达最大的点为鞍点，不过我不知道该怎么证明.

称此路径为MEP(minimum energy path).

path的逼近

上面的那个问题自然是很难求解的，所以不得不去寻找一个替代.

Mechanical Model

假设已经有一组点$p_i$(N+2)个, $p_0=\theta_0, p_{N+1}=\theta_2$, 考虑下式:

\[E(p)=\sum_{i=1}^N L(p_i) + \sum_{i=0}^N \frac{1}{2}k\|p_{i+1}-p_i\|^2,
\]

其中，$k$是人为设定的值.

当$k$很小的时候，高能量(损失)的点之间的距离会拉大. 关于这个论点我有一点存疑，因为我觉得如果$k$真的很小很小，那么$p_i$应该会缩在一起吧，比如俩端. 当$k$过大的时候，路径会被缩短和拉紧(像弹簧)，这点我是认同的，因为$p_0, p_{N+1}$之间的线段会最短，这个肯定是不会太好的，因为会错过"鞍点".

Nudged Elastic Band

一个改进的版本是:

\[F_i = -\nabla_{p_i} E(p)=F_i^L+F_i^S,
\]

即把$E(p)$分成了俩个部分, 进一步:

\[F_i^{NEB}=F_i^L|_{\perp}+F_i^S|_{\parallel}.
\]

也就是说，认为第一部分$\sum L(p_i)$只提供一个垂直的力，而剩下的一部分只提供一个平行的力，就像一根弹性绳一样，一方面有一个上下拉扯的力，另一方面有一个水平伸缩的力.

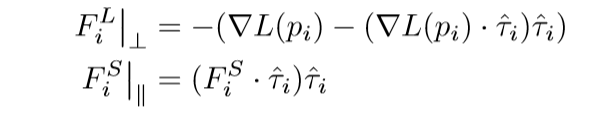
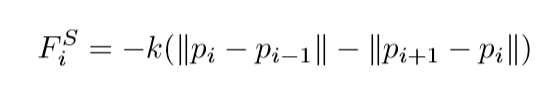
其中$\hat{\tau}_i$是路径的切线方向. 如何定义这个方向呢:

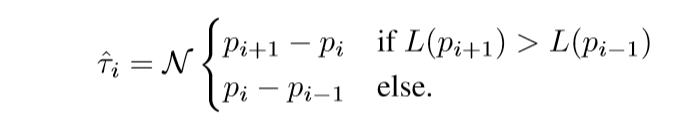
$\mathcal{N}(x)$将$x$归一化.

作者说，这么做，使得不会出现拉紧的情况了，值得商榷.

算法:

我奇怪的一点是，为什么更新$p_i$的时候，只受到$F_i^L|_{\perp}$的作用，切线方向的力呢?

还有一个AutoNEB, 这个算法就是上面的扩展，使得我们自动增加点$p_i$.

局部最优

作者说，通过上面的算法，往往会找到局部最优的MEP，但是呢，通过某些方法，我们也能使得这些局部最优显得可靠.

假设$A, B, C$三个点，代表了三个最小的参数点, 而且我们有了局部最优的路径$L_{AB}, L_{BC}$, 那么:

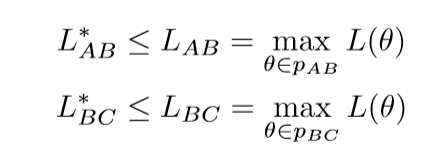
这个结论是显然的, 另外:

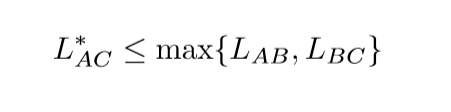
这个什么意思呢，就是$A\rightarrow B \rightarrow C$也是$A \rightarrow C$的一个路径，所以自然有上式成立.

这个有什么用呢?

假设我们有很多个最小值点$t_1, \ldots, t_N$, 先利用算法找到$t_1$到$t_2, \ldots, t_N$的路径，这个就像一棵树(论文用树来表示，其实图更恰当吧). 可能绝大部分都是局部最优的，如何判断这些局部最优的优劣性. 首先，选出每一条路径中的最大能量点(“鞍点”)$c_2, \ldots, c_N$, 不妨设$t_1 \rightarrow t_k$的路径拥有这些点中最大的，也就是最坏的一个路径. 我们可以试着从$t_k$往其它的寻找路径，如果能够找到一个路径(假设为$t_j$), $t_k \rightarrow t_j$，使得$t_1 \rightarrow t_j \rightarrow t_k$比直接$t_1 \rightarrow t_k$更优，那么我们就找到一个更好的路径，将其替换，以论下来，再对次劣的进行操作...

这样子，我们就能够有足够的理由相信，这些局部最优的路径是可靠的.

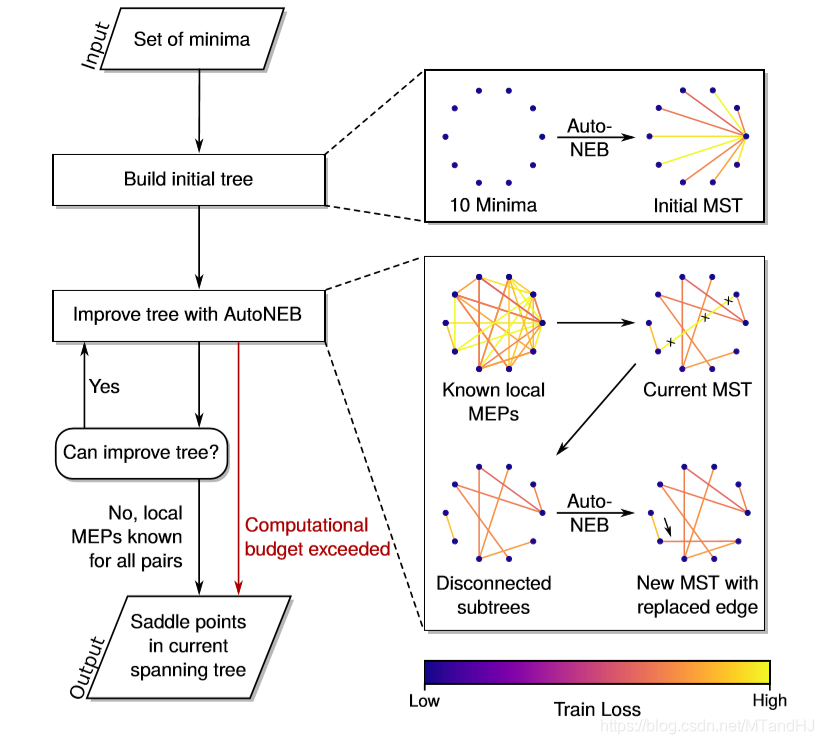
经过实验，作者发现，越深，越宽(每层的神经元个数)的网络，最优点之间的MEP越会展现出无障碍平坦的性质，即普遍的小损失.

如果确实如此，那么我们就容易构造一族解，这样网络就更灵活了不是？