Chapter 2 Randomized Experiments

目录

• 概
• 2.1 Randomization
• 2.2 Conditional randomization
• 2.3 Standardization
• 2.4 Inverse probability weighting
• Technical Point 2.2 Formal definition of IP weights
• Technical Point 2.3 Equivalence of IP weighting and standardization

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

概

计算causal effect的一个令人头疼的地方就在于, 往往对于一个个体来讲, 我们是无法同时观测到\(Y^0, Y^1\)的, 毕竟一个人如果做了心脏迁移手术(\(A=1\)), 则我们就无法得知\(Y^0\), 反之亦然.

2.1 Randomization

要知道, 计算\(\mathrm{Pr}(Y^a)\), 等价于

\[\sum_b \mathrm{Pr}(Y^a|A=b)\mathrm{Pr}(A=b),
\]

由于最开始讲的缘故, 我们很难通过模拟实验通过上式子来计算causal effect.

但是, 如果\(A\)是纯随机选择的, 与\(Y^a\)无关, 则我们有

\[\mathrm{Pr}(Y^a|A) = \mathrm{Pr}(Y^a),
\]

则我们能够很容易地计算出causal effect了.

这个在实际模拟实验中, 便是指, 对于任意一个个体, 我们抛一枚与其无关的硬币来判断其是否进行\(A=1\).

不过需要注意的是, \(Y\)与\(A\)依然不是独立的, 这是因为\(Y\)需要根据\(A\)来选择需要表现出\(Y^0\)或者是\(Y^1\).

\(Y^a\)与\(A\)是独立的, 我们记为\(Y^a \amalg A\).

因为markdown没法用\upmodels这个符号, 就姑且用\amalg来代替了.

2.2 Conditional randomization

自然的, 我们可以在条件\(L\)寻找一个

\[Y^a \amalg A | L.
\]

即, \(\mathrm{Pr}(Y^a|A,L) = \mathrm{Pr}(Y^a|L)\).

在实际的模拟实验中, 即\(A\)根据\(L\)的不同可以进行选择, 但与\(Y^a\)没有任何关系.

上面的两种随机实验的情况, 都是为了满足可交换性, 即exchangeability, 更具体的一个是边际性质的, 一个是条件性质的.

2.3 Standardization

那么根据我们的模拟实验如何计算causal effect呢?

一种方法是standardization, 实际上就是普通的全概率公式.

\[\sum_{l} \mathbb{E}[Y|L=l,A=a] \cdot \mathrm{Pr} [L=l].
\]

2.4 Inverse probability weighting

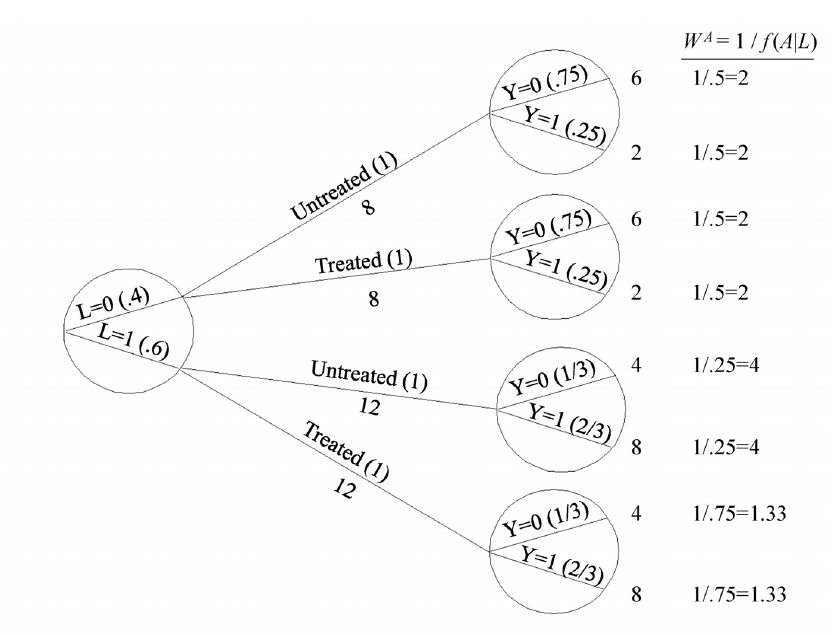
设想, 计算\(\mathrm{Pr}[Y^a]\), 实际上就只需要知道这个群体的每个个体的\(Y^a\)即可.

现在, 假设我们想要知道\(Y^0\), 但是在模拟实验中一部分是treated\((A=1)\), 所以, 我们需要知道\((A=1)\)的人的\(Y^0\)如何. 假设对这批样本进行的是untreated\((A=0\)), 则因为可交换性, 我们可以得知,

\[\mathrm{Pr}[Y^0|A=1,L=l] = \mathrm{Pr} [Y^0|A=0,L=l],
\]

所以只是单纯的\(\mathrm{Pr}[A=1,L=l]\)乘上右项而已.

可以公式化表示为

\[\mathbb{E} [ \frac{I(A=a)Y}{f[A|L]}],
\]

容易证明这个式子和上面的standardization实际上是一致的.

不过需要注意的是, 这个方法只适用于\(A\)是离散的时候.

Technical Point 2.2 Formal definition of IP weights

p23

Technical Point 2.3 Equivalence of IP weighting and standardization

p24

这个technical 讨论了IP weighting 和 standardization 的等价性以及适用条件, 这里特别注明, 当\(A\)是连续的时候, 且\(f(A|L)\)表示概率密度的时候:

\[\mathbb{E} [ \frac{I(A=a)Y}{f[A|L]}] = \mathbb{E} \{\mathbb{E}[\frac{I(A=a)}{f(a|L)}|L]\mathbb{E}[Y^a|L]\} = \mathbb{E}[\mathrm{Pr}[A=a|L]\mathbb{E}[Y^a|L]] = 0.
\]

最后等于0是因为\(\mathrm{Pr}(A=a|L)=0\).