31、下一个排列 | 算法（leetode，附思维导图 + 全部解法）300题

零 标题：算法（leetode，附思维导图 + 全部解法）300题之（31）下一个排列

一 题目描述

二 解法总览（思维导图）

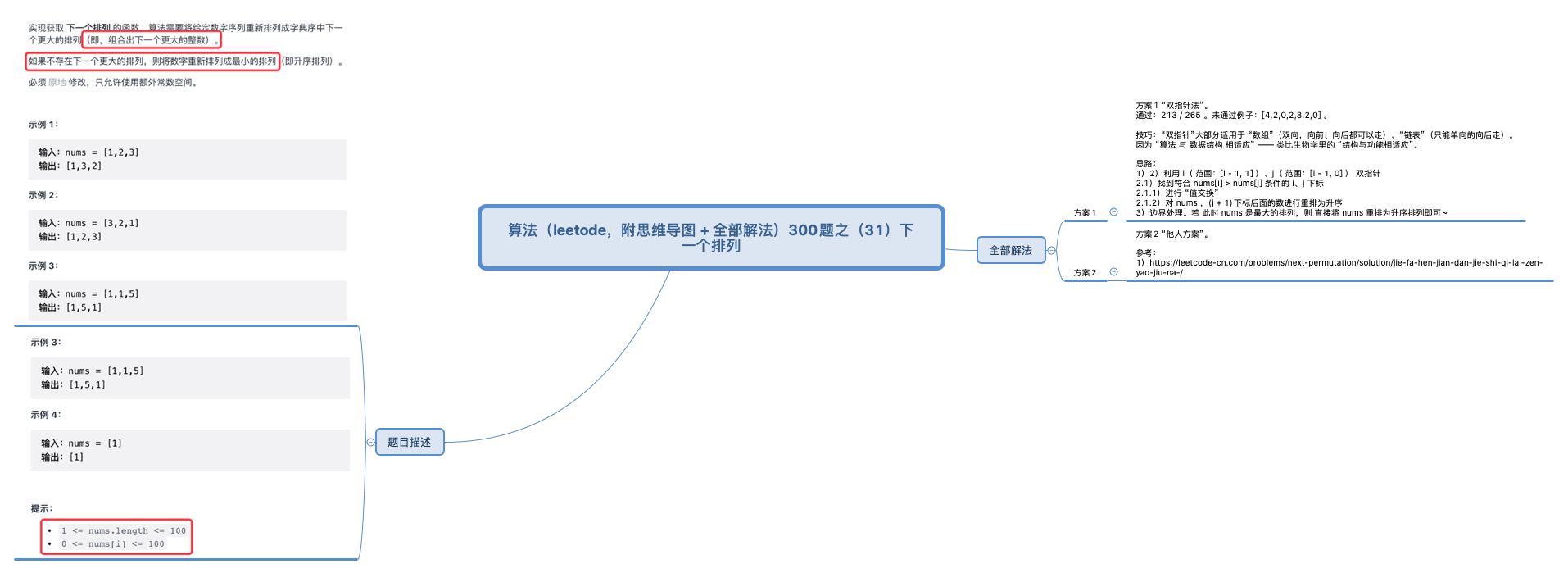
三 全部解法

1 方案1

1)代码：

// 方案1 “双指针法”。
// 通过：213 / 265 。未通过例子：[4,2,0,2,3,2,0] 。

// 技巧：“双指针”大部分适用于 “数组”（双向，向前、向后都可以走）、“链表”（只能单向的向后走）。
// 因为 “算法 与 数据结构 相适应” —— 类比生物学里的 “结构与功能相适应”。

// 思路：
// 1）2）利用 i（ 范围：[l - 1, 1] ）、j（ 范围：[i - 1, 0] ） 双指针
// 2.1）找到符合 nums[i] > nums[j] 条件的 i、j 下标
// 2.1.1）进行 “值交换”
// 2.1.2）对 nums ，(j + 1)下标后面的数进行重排为升序
// 3）边界处理。若 此时 nums 是最大的排列，则 直接将 nums 重排为升序排列即可~
var nextPermutation = function(nums) {
    // 1）状态初始化
    const l = nums.length;

    // 2）利用 i（ 范围：[l - 1, 1] ）、j（ 范围：[i - 1, 0] ） 双指针
    for (let i = l - 1; i >= 1; i--) {
        for (let j = i - 1; j >= 0; j--) {
            // 2.1）找到符合 nums[i] > nums[j] 条件的 i、j 下标
            if (nums[i] > nums[j]) {
                // 2.1.1）进行 “值交换”
                [nums[i], nums[j]] = [nums[j], nums[i]];
                // 2.1.2）对 nums ，(j + 1)下标后面的数进行重排为升序
                let tempList = nums.slice(j + 1);
                tempList.sort((a, b) => a - b);
                nums.splice(j + 1, (l - j - 1), ...tempList);
                return;
            }
        }
    }

    // 3）边界处理。若 此时 nums 是最大的排列，则 直接将 nums 重排为升序排列即可~
    nums = nums.sort((a, b) => a -b);
};

2 方案2

1)代码：

// 方案2 “他人方案”。

// 参考：
// 1）https://leetcode-cn.com/problems/next-permutation/solution/jie-fa-hen-jian-dan-jie-shi-qi-lai-zen-yao-jiu-na-/
var nextPermutation = function(nums) {
    const l = nums.length;
    let i = l - 2;

    // 从右往左遍历拿到第一个左边小于右边的 i,此时 i 右边的数组是从右往左递增的
    while (i >= 0 && nums[i] >= nums[i+1]){
        i--;
    }

    if (i >= 0){
        let j = l - 1;
        // 从右往左遍历拿到第一个大于nums[i]的数,因为之前nums[i]是第一个小于他右边的数，所以他的右边一定有大于他的数
        while (j >= 0 && nums[j] <= nums[i]){
            j--;
        }
        // 交换两个数
        [nums[j], nums[i]] = [nums[i], nums[j]]
    }

    // 对 i 右边的数进行交换
    // 因为 i 右边的数原来是从右往左递增的，把一个较小的值交换过来之后，仍然维持单调递增特性
    // 此时头尾交换并向中间逼近就能获得 i 右边序列的最小值
    let left = i + 1;
    let right = l - 1;
    while (left < right){
        [nums[left], nums[right]] = [nums[right], nums[left]]
        left++
        right--
    }
}