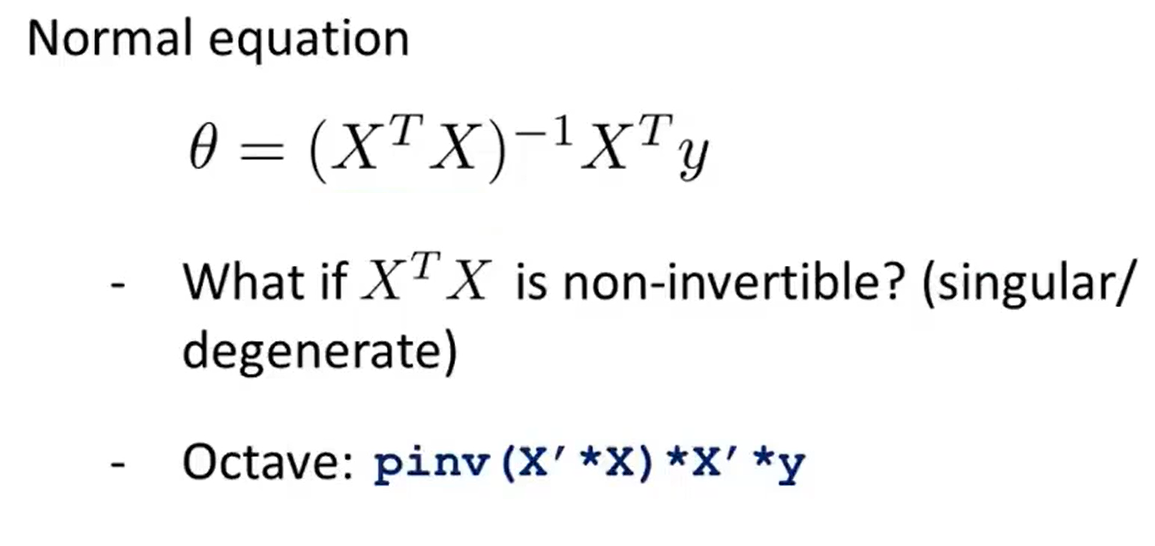Machine learning(4-Linear Regression with multiple variables )
1、Multiple features
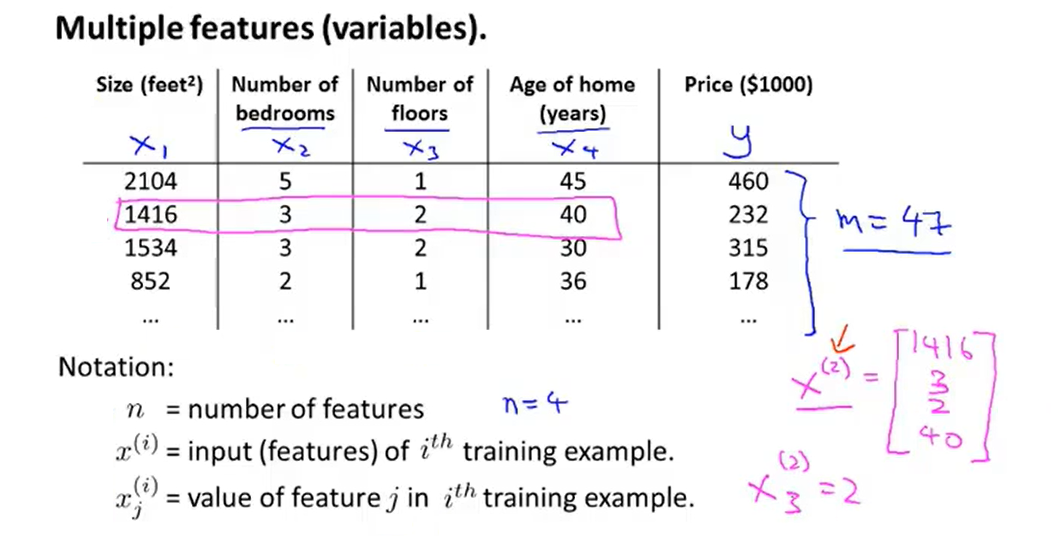
- So what the form of the hypothesis should be ?
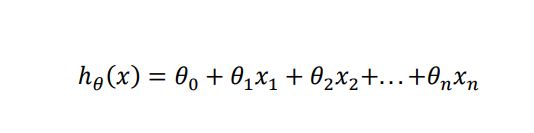
- For convenience, define x0=1
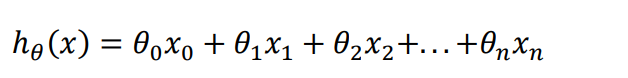
- At this time, the parameter in the model is a ( + 1)-dimensional vector, and any training instance is also a ( + 1)-dimensional vector. The dimension of the feature matrix is { ∗ ( + 1)} , so the formula can be simplified to :

2、Gradient descent for multiple variables
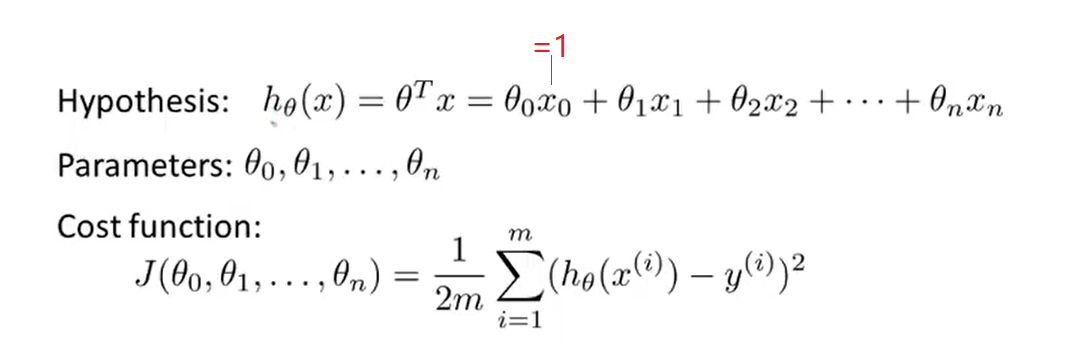
- Here is the gradient descent looks like

- Python code:
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X)
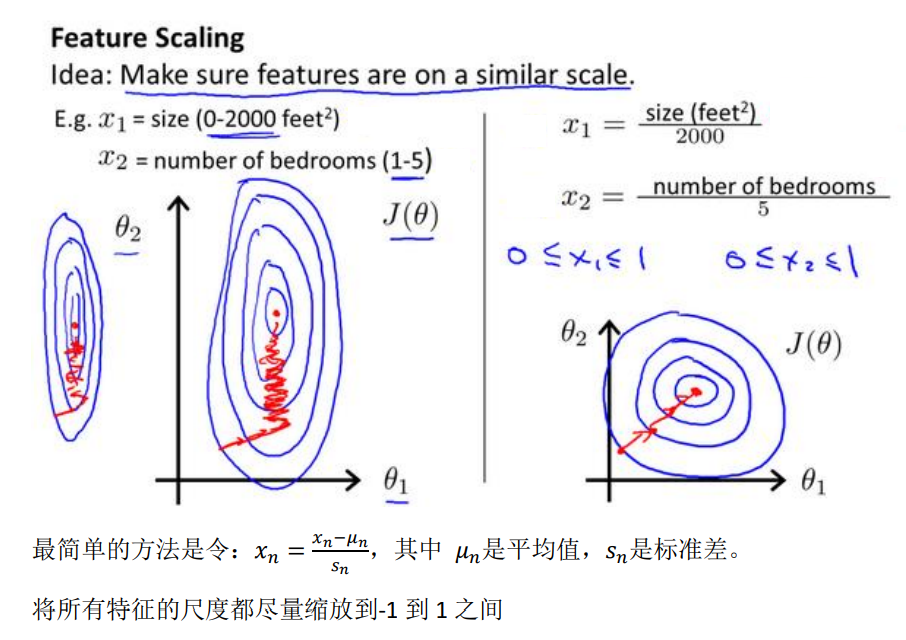
3、Gradient descent in practice I :Feature Scaling
- An idea about feature scaling(特征缩放) --- make sure features are on a similar scale and get every feature into approximately a -1≤xi≤1 range
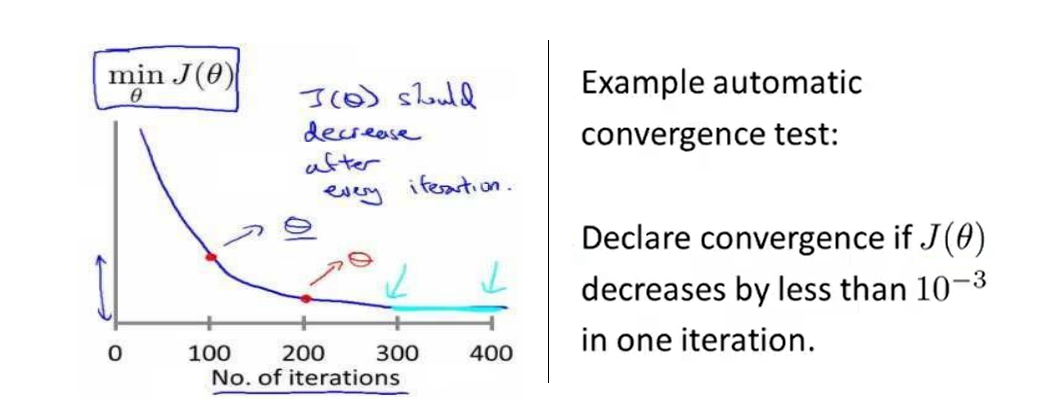
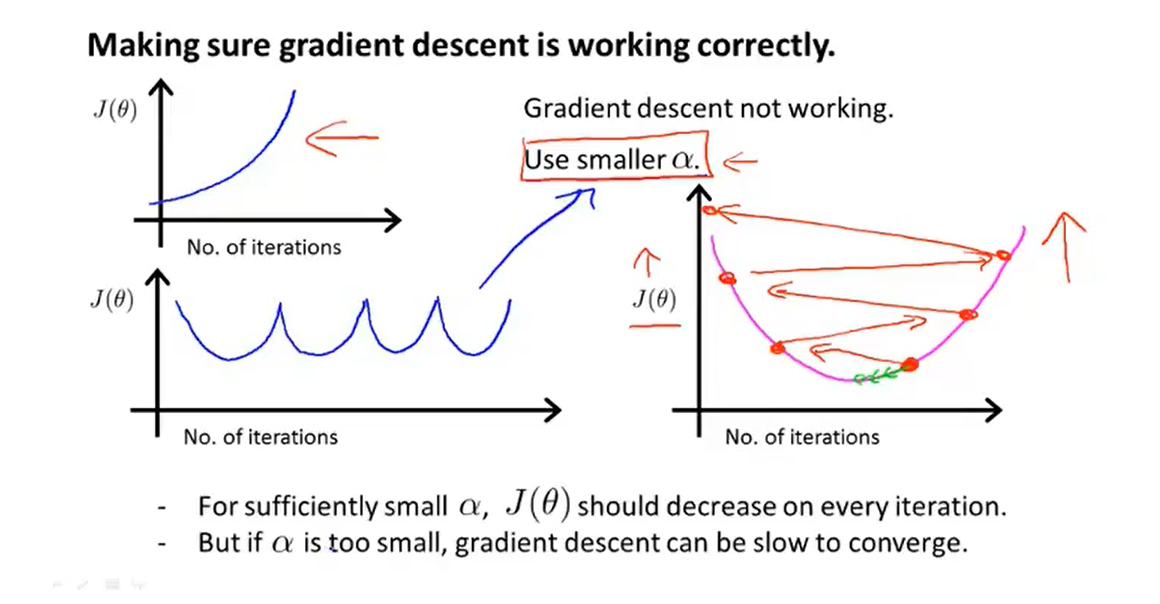
4、Gradient descent in practice II: Learning rate
5、Features and Polynomial Regression
- Housing price prediction

- Linear regression is not suitable for all data, sometimes we need a curve to fit our data, such as a quadratic model :
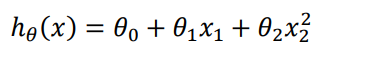
- Or maybe a cubic model :
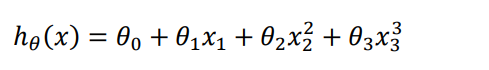
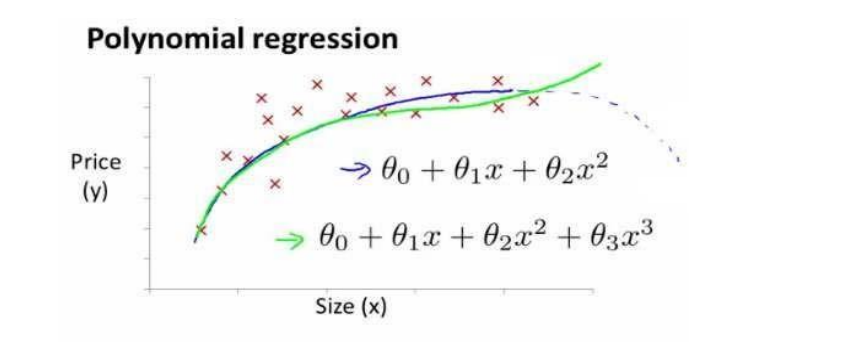
- According to the graphical characteristics of the function, we can also use :
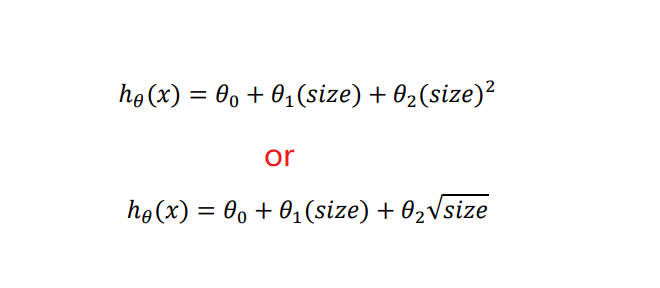
6、Normal Equation
- Normal equation : method to solve for θ analytically
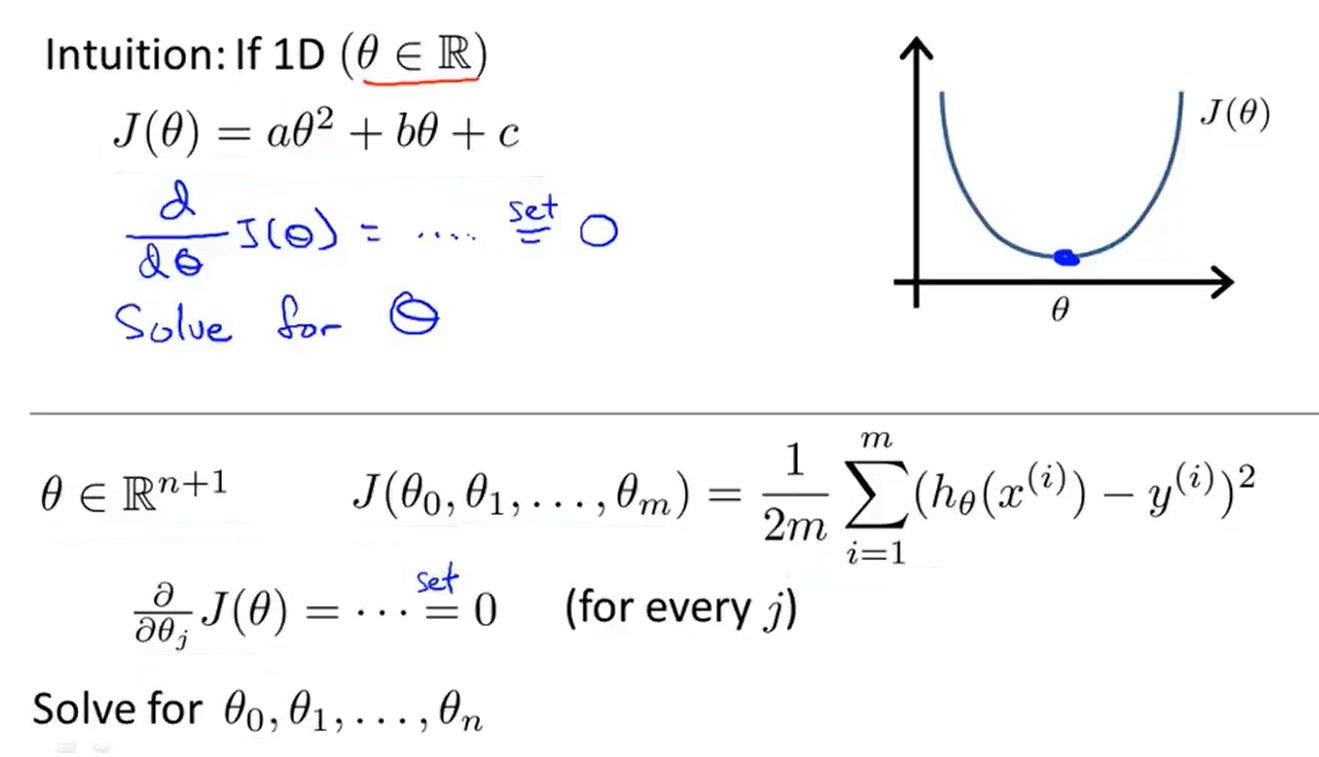
- It is too long and involved
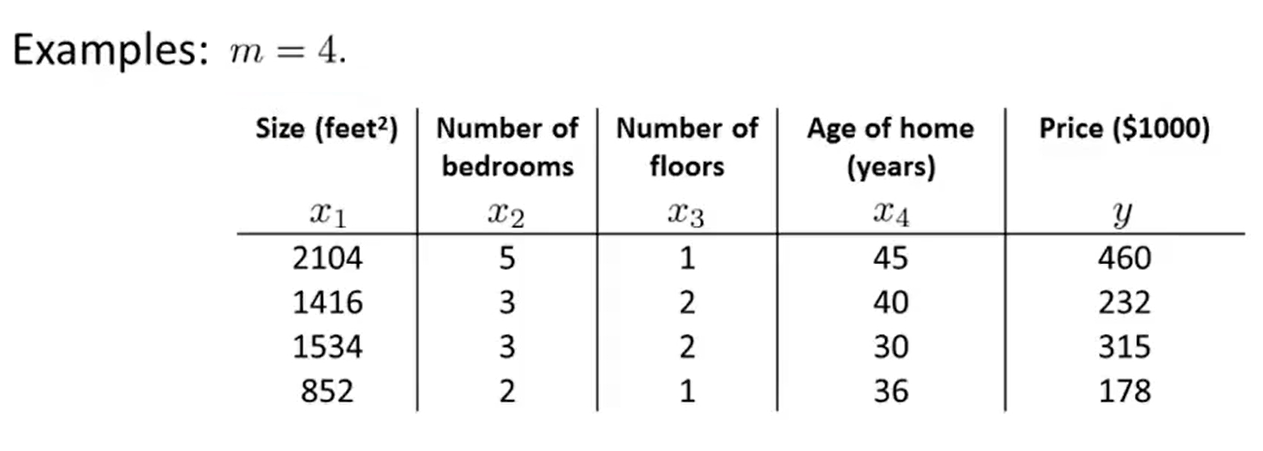
- And now,I am going to take the dataset and add an extra column
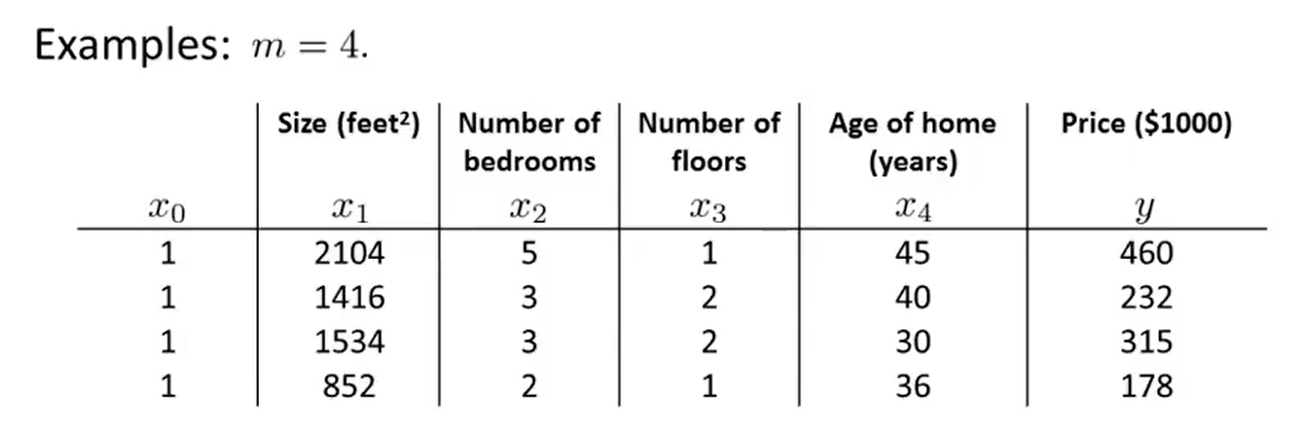
- Then construct a matrix X :

- And construct a vector y :
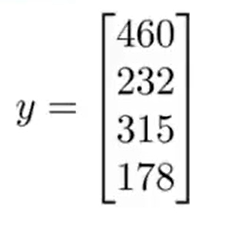
- Solve the vector using the normal equation :
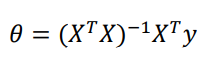
- We get :
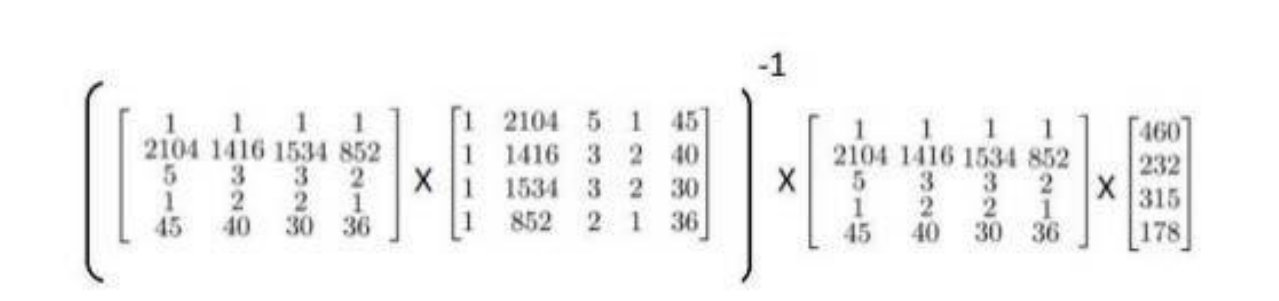
pinv(X'*X)*X'*y
- How to choose gradient descent or normal equation ?
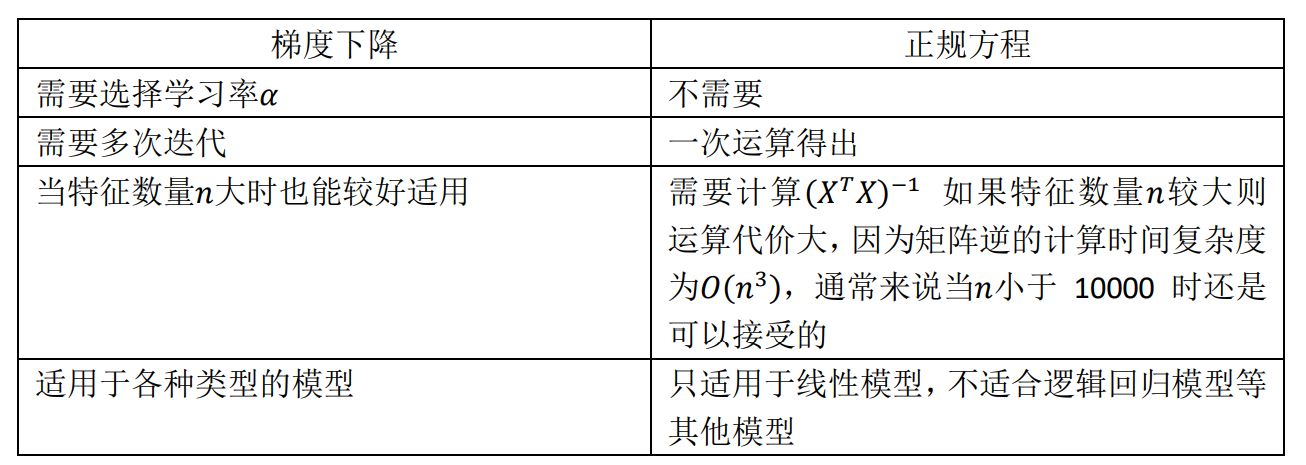
- Use python to implement Normal Equation
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X 等价于 X.T.dot(X)
return theta
7、Normal Equation Non-invertibility
8、Supplement

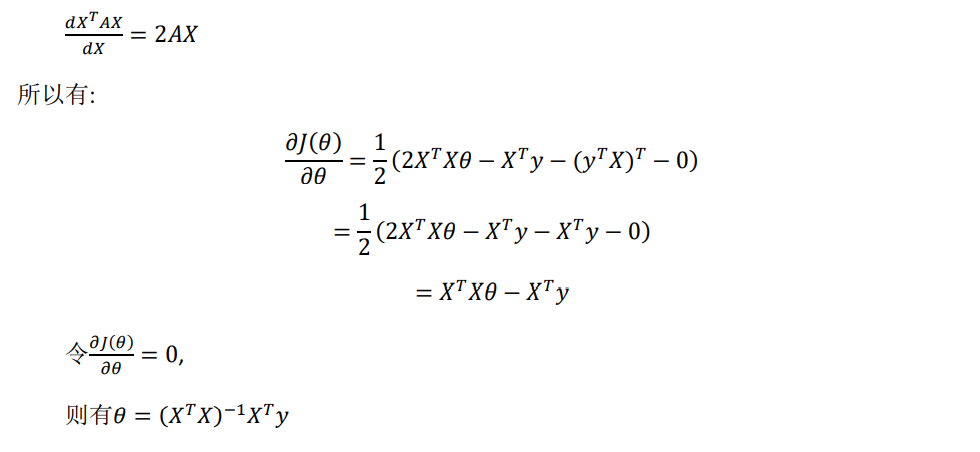
Machine learning(4-Linear Regression with multiple variables )的更多相关文章
- Machine Learning No.2: Linear Regression with Multiple Variables
1. notation: n = number of features x(i) = input (features) of ith training example = value of feat ...
- 机器学习之多变量线性回归(Linear Regression with multiple variables)
1. Multiple features(多维特征) 在机器学习之单变量线性回归(Linear Regression with One Variable)我们提到过的线性回归中,我们只有一个单一特征量 ...
- [Machine Learning] 多变量线性回归(Linear Regression with Multiple Variable)-特征缩放-正规方程
我们从上一篇博客中知道了关于单变量线性回归的相关问题,例如:什么是回归,什么是代价函数,什么是梯度下降法. 本节我们讲一下多变量线性回归.依然拿房价来举例,现在我们对房价模型增加更多的特征,例如房间数 ...
- ML:多变量线性回归(Linear Regression with Multiple Variables)
引入额外标记 xj(i) 第i个训练样本的第j个特征 x(i) 第i个训练样本对应的列向量(column vector) m 训练样本的数量 n 样本特征的数量 假设函数(hypothesis fun ...
- Machine Learning – 第2周(Linear Regression with Multiple Variables、Octave/Matlab Tutorial)
Machine Learning – Coursera Octave for Microsoft Windows GNU Octave官网 GNU Octave帮助文档 (有900页的pdf版本) O ...
- Andrew Ng Machine Learning 专题【Linear Regression】
此文是斯坦福大学,机器学习界 superstar - Andrew Ng 所开设的 Coursera 课程:Machine Learning 的课程笔记. 力求简洁,仅代表本人观点,不足之处希望大家探 ...
- CheeseZH: Stanford University: Machine Learning Ex5:Regularized Linear Regression and Bias v.s. Variance
源码:https://github.com/cheesezhe/Coursera-Machine-Learning-Exercise/tree/master/ex5 Introduction: In ...
- 机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables)
机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables) 同样是预测房价问题 如果有多个特征值 那么这种情况下 假设h表示 ...
- Linear regression with multiple variables(多特征的线型回归)算法实例_梯度下降解法(Gradient DesentMulti)以及正规方程解法(Normal Equation)
,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, , ...
- 机器学习 (二) 多变量线性回归 Linear Regression with Multiple Variables
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...
随机推荐
- Flex语法和常用鼠标手势
Flex弹性和模型 1.display : flex/inline-flex ;(设置给氟元素) flex : 将对象作为弹性伸缩盒显示: inline-flex : 将对象作为内联块级弹性伸缩显示: ...
- 在 vue-cli 项目中 使用elementUI 的“自定义主题”功能
1.安装elementUI $ npm i element-ui -S 2.安装主题工具 npm i element-theme -g 3.安装chalk主题 npm 安装 npm i element ...
- 关于AS下Gradle安装问题总结
在之前安装AS的随笔中简单描述了解决方法,但不够详细,在第二次创建项目时又遇到了gradle安装错误,通过在网上查找解决方法,发现方法比较多样,且描述不够仔细,本随笔将详细记录我在gradle安装中的 ...
- 朴素贝叶斯原理、实例与Python实现
初步理解一下:对于一组输入,根据这个输入,输出有多种可能性,需要计算每一种输出的可能性,以可能性最大的那个输出作为这个输入对应的输出. 那么,如何来解决这个问题呢? 贝叶斯给出了另一个思路.根据历史记 ...
- jmeter加密解密(加密篇)
最近刚好在弄jmeter加密解密,可以分享下.(有一段时间没写了,有点不知道从何写起,这篇写的有点乱o(╥﹏╥)o) 需求是:接口中的请求体的部分参数需要先加密再请求,返回的结果中部分字段需解密. 1 ...
- HTML在网页上不能显示图片问题
我遇到的问题是写了一个HTML程序,结果在网页上面不能显示,原因是图片路径放置错了. 修改前代码: <!DOCTYPE html> <html> <head> &l ...
- python3使用imaplib获取邮件
imaplib 获取邮件,email解析邮件config文件中存有路径 1 # config.py 2 FILE_PATH_PREFIX = os.getcwd() + '/static/' 3 FI ...
- DeDeCMS v5.7 漏洞复现
DedeCMS V5.7 漏洞复现 XSS漏洞 首先我们在首页要进行用户的注册以及登录 这里我们已经提前注册过了,登录即可 普通用户账号密码:root/passwd 管理员账号密码:admin/pik ...
- 生动直观的Gif图告诉你如何安装Python安装第3方库,在线安装离线安装全都搞定
前言 学Python的小伙伴都知道,Python学习过程中需要装不少的第3方的库,今天就和大家一起分享下第3方库的安装方法 在线安装(推荐安装式式) 点开Pycharm--file--Project- ...
- Python3入门系列之-----元组
元组 Python 的元组与列表类似,不同之处在于元组的元素不能修改 元组使用小括号,列表使用方括号 元组创建很简单,只需要在括号中添加元素,并使用逗号隔开即可 实例 tup1 = (1,2,3,4, ...