OO面向对象第三次作业总结

面向对象第三次作业总结

一、JML基础梳理及工具链

注释结构

• 行注释：//@annotation
• 块注释：/*@ annotation @*/

两种注释都是放在被注释部分上面。

常见表达式

1. 原子表达式

   1. \result表达式：表示一个方法执行所获得的结果，即方法执行后的返回值。这里此表达式的类型根据被注释的函数的返回值而定。
   2. \old(expr)表达式：用来表示一个表达式expr在相应方法执行前的取值。当expr有被修改时，使用此表达式，表示expr被修改之前的值。这里有一点需要注意，对于一个引用对象，只能判断引用本身是否发生变化，即只能描述引用对象的地址是否发生变化，而不能描述对象的成员变量等是否发生变化。
   3. \not_assigned(x,y,…)表达式：用来表示括号中的变量是否在方法执行过程中被赋值。
   4. \not_modified(x,y,…)表达式：限制括号中的变量在方法执行期间的取值未发生变化。
   5. \nonnullelements(container)表达式:表示container对象中存储的对象不会有null。

2. 量化表达式

   1. \forall表达式`：全称量词修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。使用的结构如下：

      以下几种表达式均有类似的使用结构。

   2. \exists表达式：与forall表达式使用结构类似，为存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。

   3. \sum表达式：返回给定范围内的表达式的和。

   4. \product表达式：返回给定范围内的表达式的连乘结果。

   5. \max表达式：返回给定范围内的表达式的最大值。

   6. \min表达式：返回给定范围内的表达式的最小值。

   7. \num_of表达式：返回指定变量中满足相应条件的取值个数。

3. 操作符

   1. 子类型关系操作符E1<:E2，如果类型E1是类型E2的子类型(sub type)，则该表达式的结果为真，否则为假。如果E1和E2是相同的类型，该表达式的结果也为真。
   2. 等价关系操作符b_expr1<==>b_expr2或者 b_expr1<=!=>b_expr2，其中b_expr1和b_expr2都是布尔表达式，这两个表达式的意思是 b_expr1==b_expr2 或者 b_expr1!=b_expr2 。
   3. 推理操作符b_expr1==>b_expr2 或者 b_expr2<==b_expr1，即数理逻辑中的蕴含运算。
   4. 变量引用操作符
      • \nothing 表示空集；
      • \everything 表示全集。

方法规格

• 前置条件(pre-condition)

  前置条件是对调用者的限制，即要求调用者确保条件为真。

• 后置条件(post-condition)

  后置条件是对方法实现者的要求，即方法实现者确保方法执行返回结果一定满足谓词的要求，即确保后置条件为真。

• 副作用范围限定(side-effects)

  1. assignable 表示可赋值
  2. modifiable 表示可修改
  3. 多数情况下二者可以交换使用

• signals子句

  signals子句的结构为signals (Exception e) b_expr，当b_expr为true时，方法会抛出括号中给出的相应异常e。signals_only子句是对signals子句的简化版本，不强调对象状态条件，强调满足前置条件时抛出相应的异常。

类型规格

• 不变式invariant

• 状态变化约束constraint

  可以认为状态变化约束比上面的不变式放宽了一定的限制，它并不要求一定不发生变化，而是在变化过程中形成要满足一定的约束条件。

二、部署SMT Solver

我的测试代码：

package test;

public class SimplePath {

    /*@ requires ints != null && ints.length > 10
      @ requires ints[0] == 1 && ints[2] = 2;
      @ ensures \result == (\num_of int i, j; 0 <= i && i < j && j < ints.length;ints[i] != ints[j]);
      @*/
    public static int getDistinctnode(int[] ints) {
        int num = 0;
        for (int i = 0;i < ints.length;i++) {
            num++;
            for (int j = 0;j < i;j++) {
                if (ints[i] == ints[j]) {
                    num--;
                    break;
                }
            }
        }
        return num;
    }

    /*@ requires ints != null && ints.length > index;
      @ requires ints[0] == 1 && ints[2] == 2;
      @ ensures \result == ints[index];
      @*/
    public static int getnode(int[] ints, int index) {
        return ints[index];
    }

    /*@ ensures result == (a + b);
      @*/
    public static int addaandb(int a, int b) {
        if (a == 2 && b == 3) {
            return 1;
        }
        return a + b;
    }
}

我的测试程序：

java -jar openjml/openjml.jar -check test/SimplePath.java

我的测试结果：

test/SimplePath.java:6: 错误: The expression is invalid or not terminated by a semicolon
      @ requires ints[0] == 1 && ints[2] = 2;
        ^
test/SimplePath.java:31: 错误: 找不到符号
    /*@ ensures result == (a + b);
                ^
  符号:   变量 result
  位置: 类 SimplePath
2 个错误

三、JML Unit自动测试

• 在jml语法方面，并不能使用exist和formal，导致实际使用价值十分有限。
• 在生成数据方面，除了能生成几个边界数字之外，不能支持ArrayList甚至int数组，只能生成空，导致测试结果没有参考价值。

我的测试代码：

package test;

public class SimplePath {

    /*@ requires ints != null && ints.length > 10;
      @ requires ints[0] == 1 && ints[2] == 2;
      @ ensures \result == (\num_of int i, j; 0 <= i && i < j && j < ints.length;ints[i] != ints[j]);
      @*/
    public static int getDistinctnode(int[] ints) {
        int num = 0;
        for (int i = 0;i < ints.length;i++) {
            num++;
            for (int j = 0;j < i;j++) {
                if (ints[i] == ints[j]) {
                    num--;
                    break;
                }
            }
        }
        return num;
    }

    /*@ requires ints != null && ints.length > index;
      @ requires ints[0] == 1 && ints[2] == 2;
      @ ensures \result == ints[index];
      @*/
    public static int getnode(int[] ints, int index) {
        return ints[index];
    }

    /*@ ensures \result == (a + b);
      @*/
    public static int addaandb(int a, int b) {
        if (a == 2 && b == 3) {
            return 1;
        }
        return a + b;
    }
}

我的测试命令：

java -jar jmlunitng.jar test/SimplePath.java

我的测试结果：

[TestNG] Running:
  Command line suite

Failed: racEnabled()
Passed: constructor SimplePath()
Passed: static addaandb(-2147483648, -2147483648)
Passed: static addaandb(0, -2147483648)
Passed: static addaandb(2147483647, -2147483648)
Passed: static addaandb(-2147483648, 0)
Passed: static addaandb(0, 0)
Passed: static addaandb(2147483647, 0)
Passed: static addaandb(-2147483648, 2147483647)
Passed: static addaandb(0, 2147483647)
Passed: static addaandb(2147483647, 2147483647)
Failed: static getDistinctnode(null)
Passed: static getDistinctnode({})
Failed: static getnode(null, -2147483648)
Failed: static getnode({}, -2147483648)
Failed: static getnode(null, 0)
Failed: static getnode({}, 0)
Failed: static getnode(null, 2147483647)
Failed: static getnode({}, 2147483647)

===============================================
Command line suite
Total tests run: 19, Failures: 8, Skips: 0
===============================================

Process finished with exit code 0

四、架构设计与重构分析

第一次作业

• 结构分析
  
  

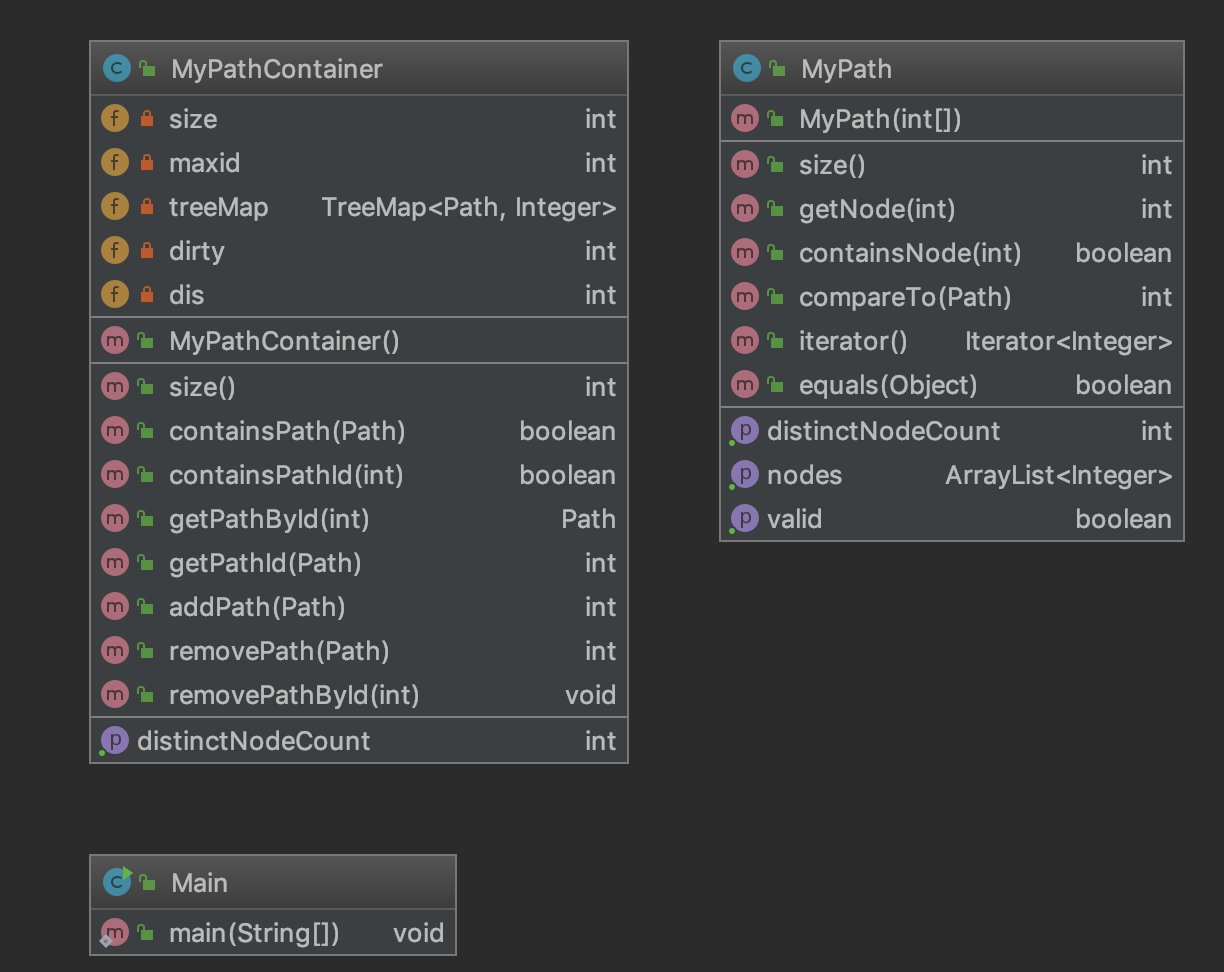
  第一次作业的结构比较简单，就是从Main调用Mypath和Mypathcontianer进行操作。

  在Mypath中主要是只有初始化时增加，初始化后就不需要变化，同时结点的顺序使用Arraylist保存。

  在Mypathcontianer中有很多查找删减，在求不同点的个数的时候甚至需要重新遍历。对于程序的优化有较大的需要。

• 复杂度与依赖度分析
  
  
  
  

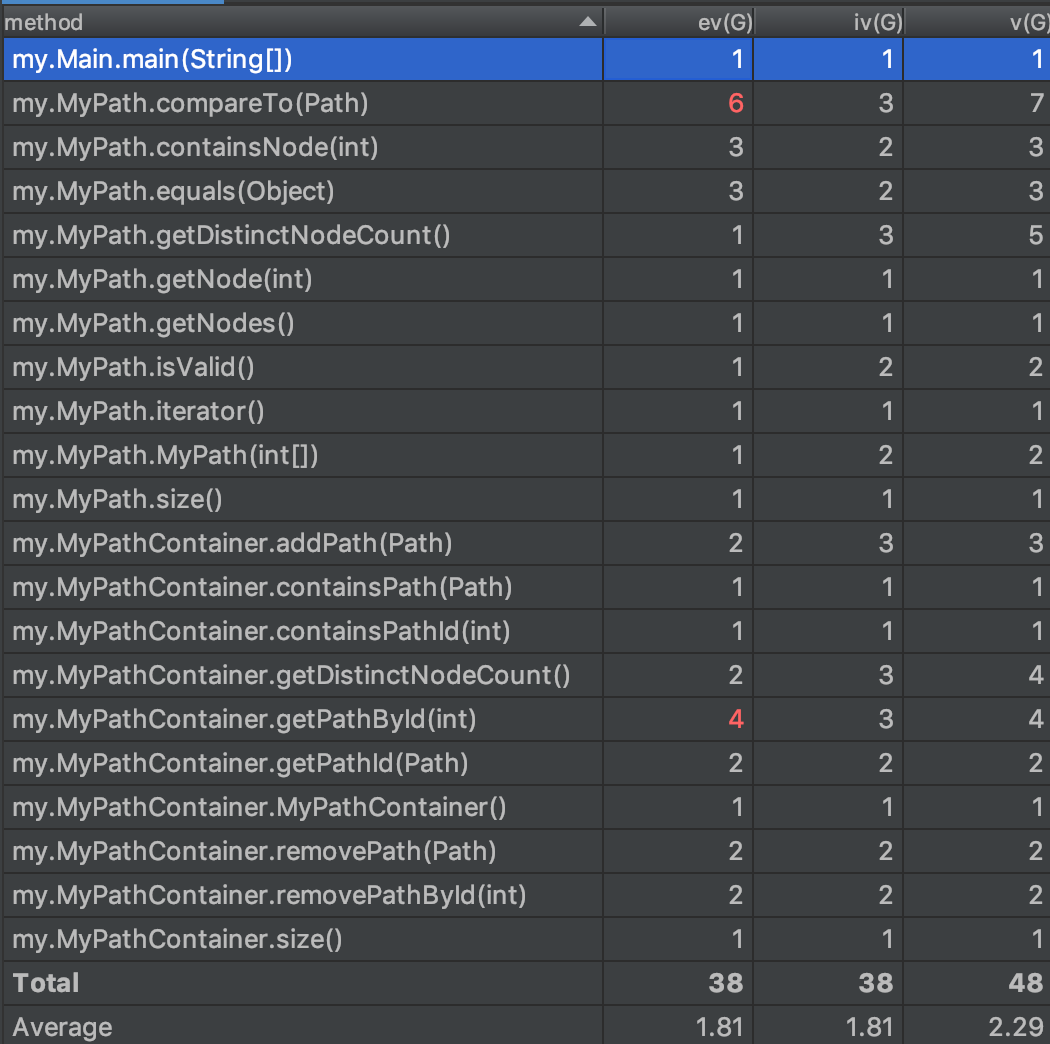
  由于第一次作业比较简单，只有compare函数比较复杂。因为此方法不得不便利对比，导致其复杂度较大。

第二次作业

• 结构分析

  在继承方面第二次作业保留了对第一次作业的继承，只是把原来的函数加了一点进一步的操作，这样就可以直接用super方法，不用复制，避免bug带来的麻烦。

  在重构方面，增加了一个对象来专门管理图，其实可以直接放在Mygraph中的，只是考虑到类的复杂度太高了，就把其剥离。我使用的是邻接表的思想来保存边，但是并不是真的用了链表，而是在每个node的对象里面放了一个Hashmap，同时借助了操作系统中的page的管理方法，记录每个边产生的次数，来更简单的管理边。

  在优化性能方面，我在每个node的对象中都有一个hashset来保存连通的点，通过BFS计算出连通的点后就不必重复计算。最短路径也是一样，每次用迪杰斯特拉计算后都会保存。为了支持图的修改，我设计了一个静态变量的int，作为当前图的version，每当图修改时，version就会增加，而每次计算出的一些中间变量都会附带当前的version，所以，只有当读取之前保存的结果且发现version不匹配时，才会重新计算。

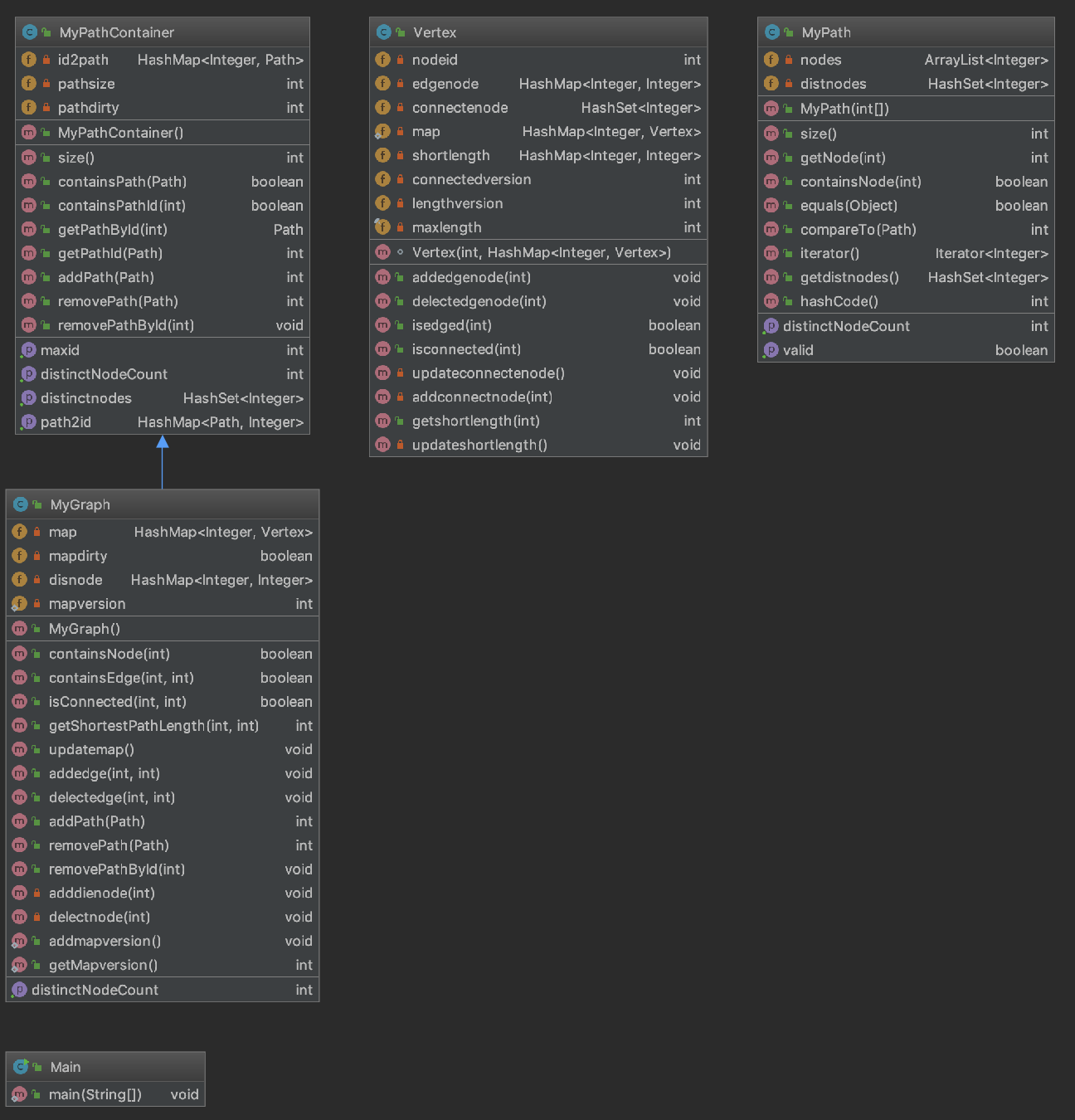
• 复杂度与依赖度分析
  
  
  
  
  
  

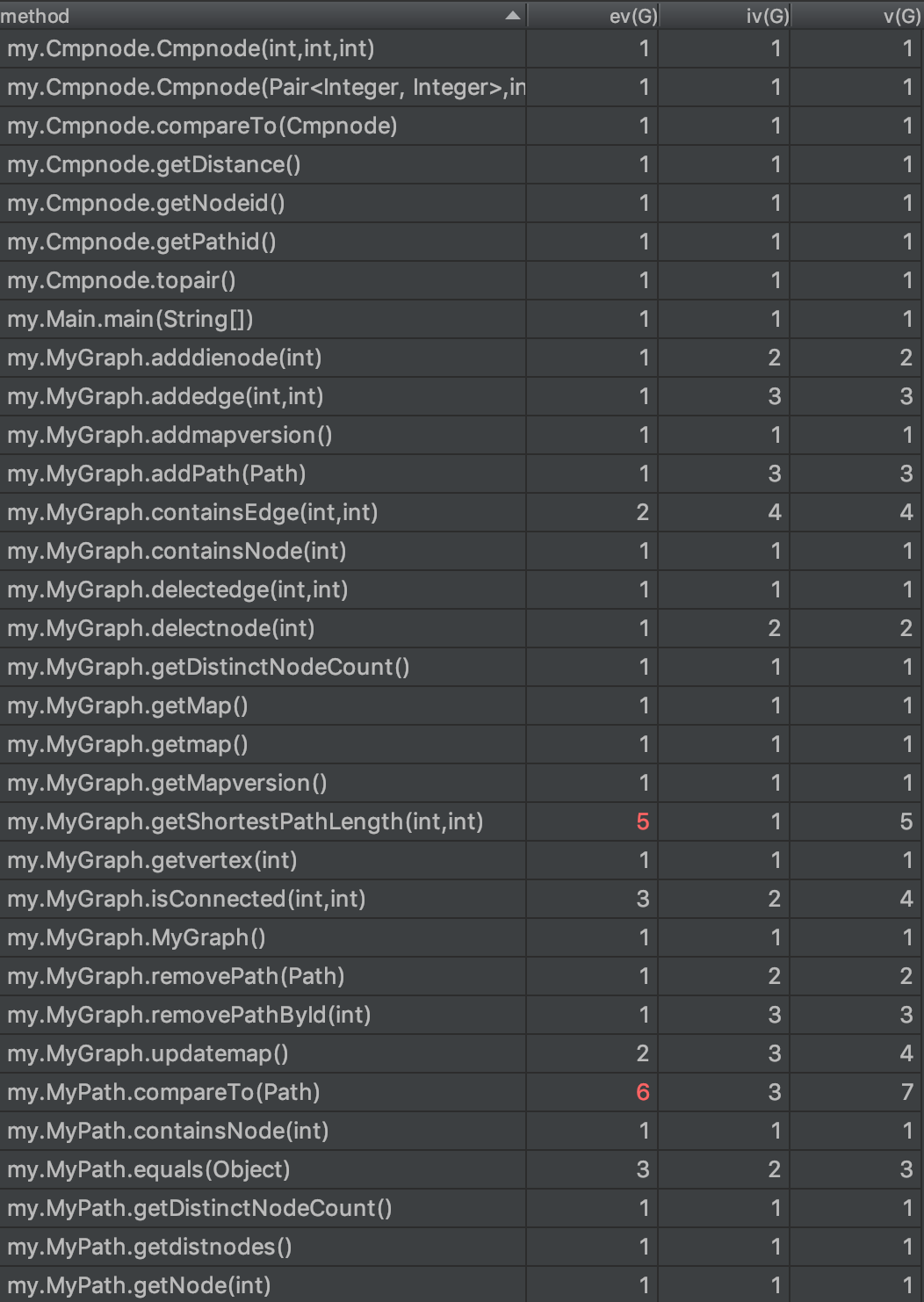
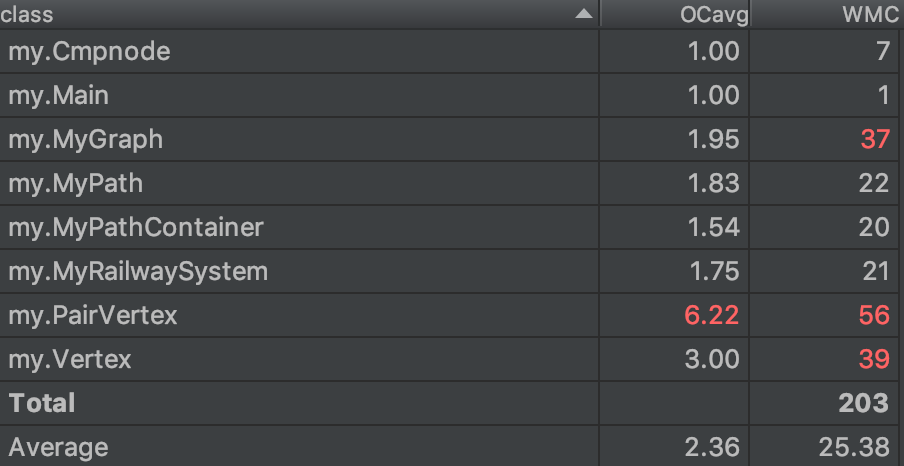
  由于本人使用了如上的更新策略，导致计算时经常需要检查version，所以依赖复杂度有所增加，不过由于我把更新机制都封存在一个方法中了，所以整体方法的复杂度不是特别高。当然由于使用了迪杰斯特拉算法，所以哪个方法的复杂度也比较高。

第三次作业

• 结构分析
  
  
  
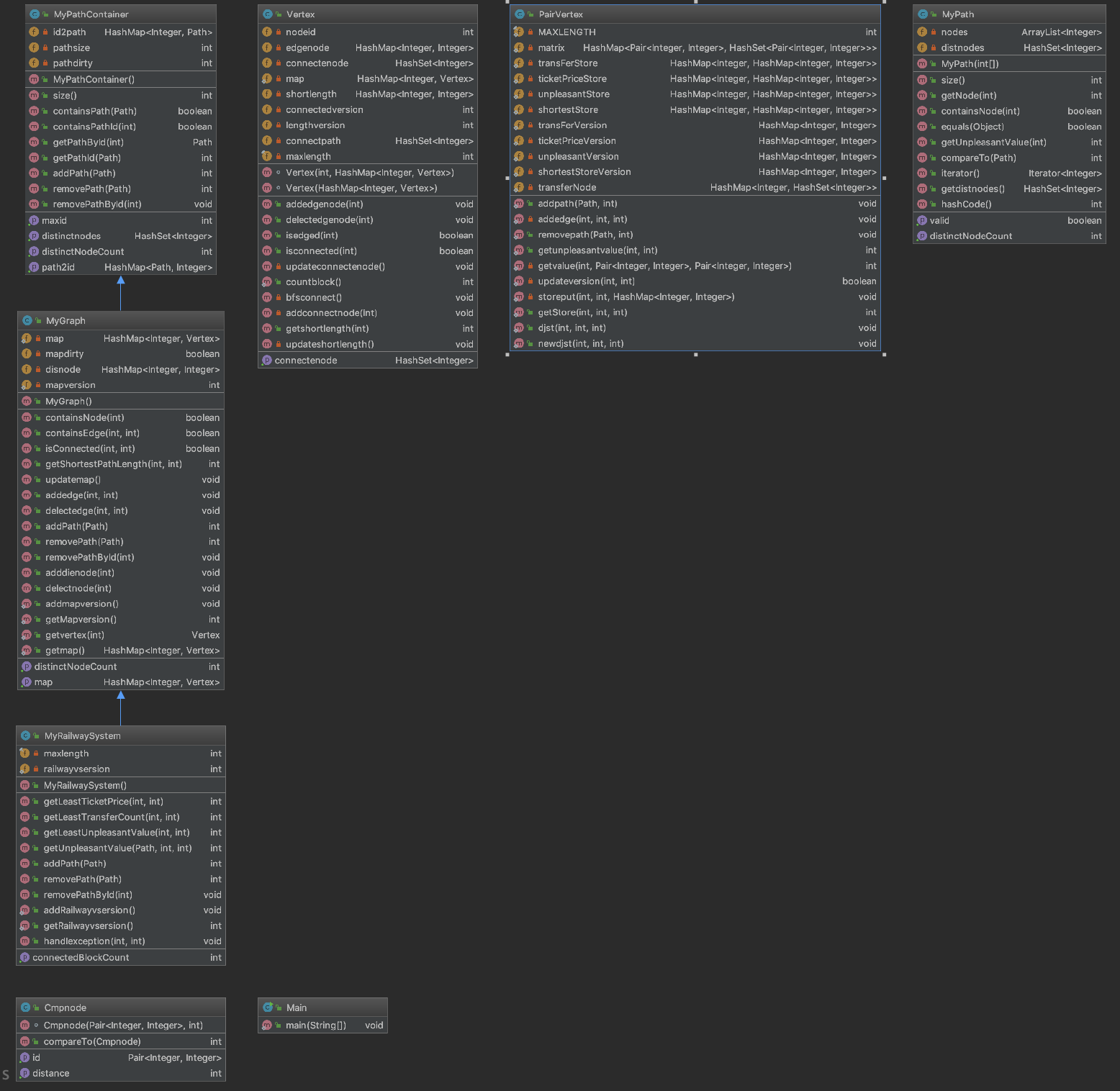
  在继承方面，第三次作业同样是继承前两次作业，只是把原来的函数加了一点进一步的操作，这样就可以直接用super方法，不用复制，避免bug带来的麻烦。但是，由于super之后改动的较多，所以强行调用super并不是完全合理，但是从减少bug和工作量的角度我还是使用了大量继承。

  在重构方面，增加了一个对象来管理地铁系统，增加一个对象在堆优化的时候代表结点。我采取了拆点的设计，把只有结点号和path号完全一样才能视作一个结点。这样的问题是在计算距离时图过于庞大。

  在优化性能方面，我把构建图和删除图都放在add和remove方法中，所以不用每次重新画图，减少了计算量，同时在迪杰斯特拉时使用了堆优化。和上一次一样我使用了version的方法保存更新计算出了各种距离值。

• 依赖度和复杂度分析
  
  
  
  
  
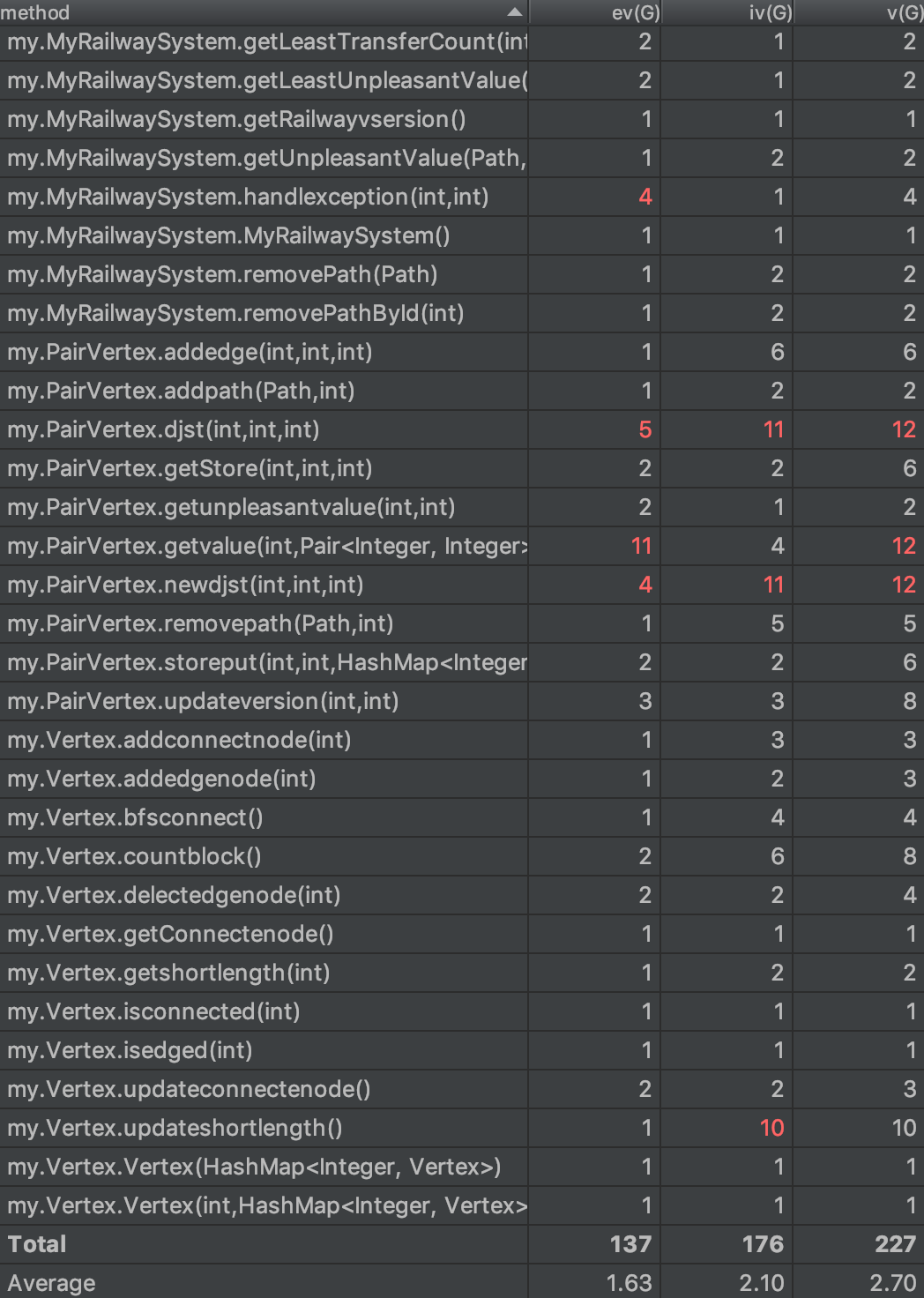
  由于很多方法都用了继承，所以很长的方法看起来复杂度也不是很高。这得益于面向对象思想在工程中的便捷性。

bug与修复

• 第一次作业

  本人课上课下都没有wronganser，但是由于刚开始没有提升效率的概念，导致强测出现了10个超时。我从以下三个方面修改优化了自己的程序：

  把计算时的便利类型的操作尽量放在add和remove这样的方法中。

  使用了Hashset来存不同的值。

  增加了保存机制，在连续两次相同计算中可以直接返回结果。

• 第二次作业

  这次作业课上课下都没有出问题，但是这次作业的程序我还有很多优化空间。

  计算连通的时候应该采用BFS而不是DFS。

  迪杰斯特拉没有使用堆优化。

  迪杰斯特拉并不是最高效的算法。

• 第三次作业

  这次作业强测和互测中都被找到了很多超时。但是我已经使用了缓存，堆优化，拆分计算等等技术。最终的发现我的问题时求路近距离是由于地铁的性质，需要考虑从同一个站点不同线路出发，导致原本n^{2的复杂度变为n}2*m。

  我的修改策略是在计算距离时新建一个点连接所有相同结点号不同路径号的点，然后从那个点开始寻找，这样算法的复杂度就是(n+1)^2。

五、规格撰写与理解的心得体会

• 使用规格的目的是在于能够用一种相对于自然语言而言更加严谨、更加没有二义性的方式对一个方法或者类的功能进行描述，这样在多人进行协作开发，而且开发的项目对于正确性与准确性的要求比较严格的时候，更能够保证不会因为不同的成员对于方法或者类的功能理解缠身歧义，导致开发过程中出错。
• 在实际体会了这种模式之后，一方面确实看到，如果确实能够做到描述严谨，JML可以对规格进行非常客观的描述，这种描述并不是实现思路，而是提供对于功能与特性的理解。但是与此同时，我也感觉到对于我来说JML其本事还是很有难度的，对于一个相对比较复杂的功能，JML的表述会显得很长，而且有时为了简化表述，还需要借助一些本来并不一定需要实现的方法，并且为这些方法还要单独写规格。感觉这样不论是书写还是理解，都会产生一定的困难，特别是当读者的编程水平并不高的时候，有可能反而因为其复杂性造成理解的偏差。因此，我觉得在一些要求比较高的特定工作领域中，使用JML更能够进行规范，但是在一些领域，比如小团队进行普通的应用开发时，个人感觉使用比较详细的自然语言更能够节约开发成本，提高效率。
• 在探索了JMLUNIT生成自动测试后，本人发现这些东西离成熟还有很遥远的距离，不光有很多JML的语法不支持，还有很多错误很难找到，且生成的测试数据并不符合实际。希望在未来的发展中这部分技术能更加完善。