【数据结构与算法Python版学习笔记】图——词梯问题 广度优先搜索 BFS

词梯Word Ladder问题

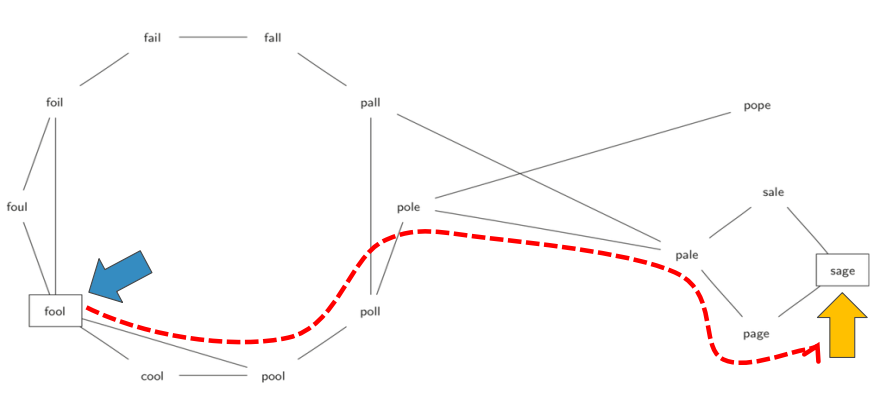
• 要求是相邻两个单词之间差异只能是1个字母，如FOOL变SAGE：

FOOL >> POOL >> POLL >> POLE >> PALE>> SALE >> SAGE

• 目标是找到最短的单词变换序列
  • 用图表示单词之间的关系；
  • 用一种名为广度优先搜索 BFS的图算法找到从起始单词到结束单词的最短路径。

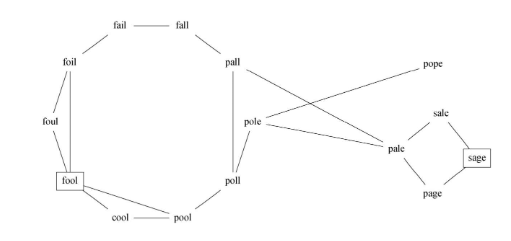
构建词梯图

算法

• 首先是将所有单词作为顶点加入图中，再设法建立顶点之间的边
• 对每个顶点（单词） ， 与其它所有单词进行比较， 如果相差仅1个字母， 则建立一条边
• 时间复杂度是O(n²)，对于所有4个字母的5110个单词，需要超过2600万次比较

优化算法

• 改进的算法是创建大量的桶， 每个桶可以存放若干单词
  • 桶标记是去掉1个字母，通配符“_”占空的单词
• 所有匹配标记的单词都放到这个桶里
  • 所有单词就位后，再在同一个桶的单词之间建立边即可
• 单词关系图是一个非常稀疏的图

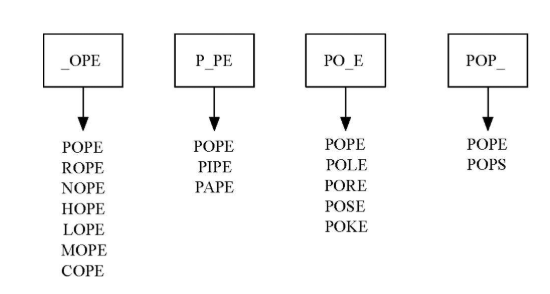
采用字典建立桶

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile, 'r')
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i]+'_'+[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]

    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1, word2)

    return g

---

广度优先搜索 BFS (breadth first search)

在单词关系图建立完成以后， 需要继续在图中寻找词梯问题的最短序列

算法思路

• 给定图G， 以及开始搜索的起始顶点s
  • BFS搜索所有从s可到达顶点的边
  • 而且在达到更远的距离k+1的顶点之前， BFS会找到全部距离为k的顶点
  • 可以想象为以s为根，构建一棵树的过程，从顶部向下逐步增加层次
  • 广度优先搜索能保证在增加层次之前，添加了所有兄弟节点到树中
• 为了跟踪顶点的加入过程， 并避免重复顶点， 要为顶点增加3个属性
  • 距离distance：从起始顶点到此顶点路径长度；
  • 前驱顶点predecessor：可反向追溯到起点；
  • 颜色color：
    • 标识了此顶点是尚未发现（白色）
    • 已经发现（灰色）
    • 还是已经完成探索（黑色）
• 还需要用一个队列Queue来对已发现的顶点进行排列
  
  决定下一个要探索的顶点（队首顶点）

算法过程

从起始顶点s开始， 作为刚发现的顶点，标注为灰色， 距离为0， 前驱为None，加入队列， 接下来是个循环迭代过程：

• 从队首取出一个顶点作为当前顶点；
• 遍历当前顶点的邻接顶点，如果是尚未发现的白色顶点，则将其颜色改为灰色（已发现），距离增加1，前驱顶点为当前顶点，加入到队列中
• 遍历完成后，将当前顶点设置为黑色（已探索过），循环回到步骤1的队首取当前顶点

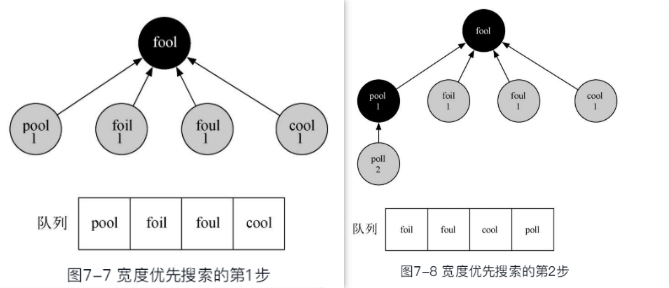
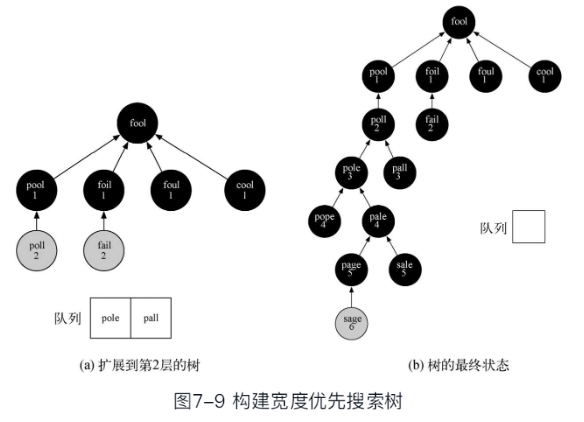
代码

• 在以FOOL为起始顶点， 遍历了所有顶点， 并为每个顶点着色、 赋距离和前驱的代码

def bfs(g, start):
    start.setDistance(0)
    start.setPred(None)
    vertQueue = Queue()
    vertQueue.enqueue(start)
    while(vertQueue.size > 0):
        currentVert = vertQueue.dequeue()
        for nbr in currentVert.getConnections():
            if(nbr.getColor() == 'white'):
                nbr.setColor('gray')
                nbr.setDistance(currentVert.getDistance()+1)
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
        currentVert.setColor('black')

• 最后，通过一个回途追溯函数来确定FOOL到任何单词顶点的最短词梯！

def traverse(y):
    x = y
    while(x.getPred()):
        print(x.getId())
        x = x.getPred()
    print(x.getId())

---

完整代码

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile, 'r')
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i]+'_'+[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]

    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1, word2)

    return g

def bfs(g, start):
    start.setDistance(0)
    start.setPred(None)
    vertQueue = Queue()
    vertQueue.enqueue(start)
    while(vertQueue.size > 0):
        currentVert = vertQueue.dequeue()
        for nbr in currentVert.getConnections():
            if(nbr.getColor() == 'white'):
                nbr.setColor('gray')
                nbr.setDistance(currentVert.getDistance()+1)
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
        currentVert.setColor('black')

def traverse(y):
    x = y
    while(x.getPred()):
        print(x.getId())
        x = x.getPred()
    print(x.getId())

if __name__ == "__main__":
    wordgrah = buildGraph("fourletterwords.txt")
    bfs(wordgrah, wordgrah.getVertex('FOOL'))
    traverse(wordgrah.getVertex('SAGE'))

---

算法分析

• BFS算法主体是两个循环的嵌套
  • while循环对每个顶点访问一次，所以是O(|V|)
  • 而嵌套在while中的for，由于每条边只有在其起始顶点u出队的时候才会被检查一次
  • 而每个顶点最多出队1次，所以边最多被检查1次，一共是O(|E|)
  • 综合起来BFS的时间复杂度为O(|V|+|E|)
• 词梯问题还包括两个部分算法
  • 建立BFS树之后， 回溯顶点到起始顶点的过程，最多为O(|V|)
  • 创建单词关系图也需要时间，最多为O(|V|2)