P1045 [NOIP2003 普及组] 麦森数

题目描述

形如2^P−1的素数称为麦森数，这时P一定也是个素数。但反过来不一定，即如果P是个素数，2^P−1不一定也是素数。

到1998年底，人们已找到了37个麦森数。最大的一个是P=3021377，它有909526位。麦森数有许多重要应用，它与完全数密切相关。

任务：从文件中输入P（1000<P<3100000），计算2^P−1的位数和最后500位数字（用十进制高精度数表示）

输入格式

文件中只包含一个整数P（1000<P<3100000）

输出格式

第一行：十进制高精度数2^P−1的位数。

第2-11行：十进制高精度数2^P−1的最后500位数字。（每行输出50位，共输出10行，不足500位时高位补0）

不必验证2^P−1与PP是否为素数。

输入输出样例

输入 #1

1279

输出 #1

386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087

分析

对于2^p,有

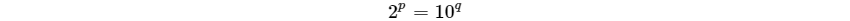
所以

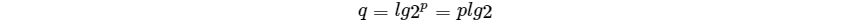
对于10^n，其位数为n+1位，故2^p的位数为

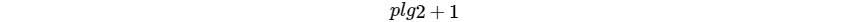
直接输出

其次就是压位高精度

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;
typedef unsigned long long Ull;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}
inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}

int a[100001];
const int Maxn = 100000;

int main()
{
    int p;
    p = Read();
    Write((int)(p*log10(2.0)+1));
    Enter;
    int left = p % 10;
    p /= 10;
    a[0] = 1;
    for(int i = 1; i <=p; i++)
    {
        for(int j = 0; j <= 100; j++)
            a[j] <<= 10;
        for(int j = 0; j <= 100; j++)
        {
            if(a[j] >= Maxn)
            {
                a[j + 1] += a[j] / Maxn;
                a[j] %= Maxn;
            }
        }
    }
    for(int i = 1; i <= left; i++)
    {
        for(int j = 0; j <= 100; j++)
            a[j] <<= 1;
        for(int j = 0; j <= 100; j++)
        {
            if(a[j] >= Maxn)
            {
                a[j + 1] += a[j] / Maxn;
                a[j] %= Maxn;
            }
        }
    }
    a[0]--;
    for(int i = 99; i >= 0; i--)
    {
        printf("%05d" , a[i]);
        if(i % 10 == 0)
            Enter;
    }
    return 0;
}