noip模拟45[真是啥也不会]

noip模拟45 solutions

真是一个题都不会了，然而考完试之后我在10min之内切掉了最后一个题

话说这是为什么呢，

因为最后一个是回滚莫队的大板子，然而我忘记了，不不不，是没有记起来过

T1 打表

好像还真的是一个打表题，找找规律就能过，真的

结论就是

\(\huge res=\frac{\sum\limits^{n}_{i=1}abs(x_i-x_{ans})}{2^k}\)

这个是可以证出来的，

首先对于只剩下一位没有选的时候，肯定是一个CPU选1，另外一个选0

我们考虑剩下更多的情况，可以知道每次两个CPU都会选择同一位进行操作，并选择不同的数

所以期望仍然是一半一半，所以还是剩下的数的差的平均数

AC_code

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
const int N=1<<18;
const ll mod=1e9+7;
ll k,ans,a[N],res;
ll ksm(ll x,ll y){
	ll ret=1;
	while(y){
		if(y&1)ret=ret*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return ret;
}
signed main(){
	scanf("%lld%lld",&k,&ans);
	for(re i=0;i<(1<<k);i++)scanf("%lld",&a[i]);
	ans=a[ans];
	for(re i=0;i<(1<<k);i++)res=(res+abs(a[i]-ans))%mod;
	printf("%lld",res*ksm(ksm(2ll,k),mod-2)%mod);
}

其实考场上没有看懂题，还找人讲了一下

T2 蛇

好象是CF的原题，我也没做过，暴搜还打错了，不知道为啥，不打了，直接正解

肯定是扭来扭去的走的，最后接上两个平着的

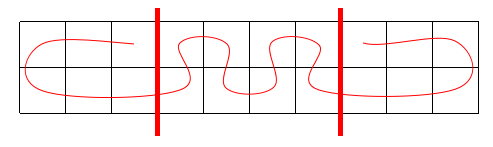
那我们就设dp[i][j][k][0/1]表示在第i行，第j列，匹配到了第k个字符

0表示可以竖着转移，1表示不可以

我们直接枚举下一个字符，转移就行了

前面的那个横着的直接预处理就好了，后面的等到dp完了之后再处理

这个处理就用hash就行了

AC_code

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ull unsigned long long
#define ll long long
const ull bas=131;
const int N=2005;
const ll mod=1e9+7;
ll n,m,dp[2][N][N][2],ans;
char ch[2][N],a[N];
ull hc[2][2][N],ha[N],ba[N];
ull get_hc0(int x,int l,int r){return hc[x][0][r]-hc[x][0][l-1]*ba[r-l+1];}
ull get_hc1(int x,int l,int r){return hc[x][1][l]-hc[x][1][r+1]*ba[r-l+1];}
ull get_ha(int l,int r){return ha[r]-ha[l-1]*ba[r-l+1];}
void get_ans(){
	memset(dp,0,sizeof(dp));
	for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)hc[i][0][j]=hc[i][0][j-1]*bas+ch[i][j]-'a';
	for(re i=0;i<=1;i++)for(re j=n;j>=1;j--)hc[i][1][j]=hc[i][1][j+1]*bas+ch[i][j]-'a';
	for(re i=0;i<=1;i++)for(re j=1;j<=n;j++){
		dp[i][j][1][0]=(ch[i][j]==a[1]);
		for(re k=2;k<=j;k++)
		if((k<<1)<=m)dp[i][j][k<<1][1]=(get_hc0(i,j-k+1,j)==get_ha(k+1,k<<1)&&get_hc1(i^1,j-k+1,j)==get_ha(1,k));
	}
	for(re k=1;k<=m;k++)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++){
		if(ch[i][j]!=a[k])continue;
		dp[i][j][k][0]=(dp[i][j][k][0]+dp[i][j-1][k-1][0]+dp[i][j-1][k-1][1])%mod;
		dp[i][j][k][1]=(dp[i][j][k][1]+dp[i^1][j][k-1][0])%mod;
	}
	for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)for(re k=0;k<=m;k++){
		if((m-k)&1)continue;
		if(m-k==2)continue;
		int mid=m-k>>1;
		if(m!=k&&(j+mid>n||get_hc0(i,j+1,j+mid)!=get_ha(k+1,k+mid)||get_hc1(i^1,j+1,j+mid)!=get_ha(k+mid+1,m)))continue;
		ans=(ans+dp[i][j][k][0]+dp[i][j][k][1])%mod;
	}
}
signed main(){
	scanf("%s",ch[0]+1);scanf("%s",ch[1]+1);n=strlen(ch[0]+1);
	scanf("%s",a+1);m=strlen(a+1);ba[0]=1;
	for(re i=1;i<=m;i++)ba[i]=ba[i-1]*bas,ha[i]=ha[i-1]*bas+a[i]-'a';
	get_ans();
	reverse(ch[0]+1,ch[0]+n+1);
	reverse(ch[1]+1,ch[1]+n+1);
	get_ans();
	if(m==1)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)ans=(ans-(ch[i][j]==a[1])+mod)%mod;
	if(m==2)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)ans=(ans+mod-(ch[i][j]==a[1]&&ch[i^1][j]==a[2]))%mod;
	printf("%lld",ans);
}

T3 购物

这个说白了也是一个结论题，我还是不会

结论：我们在K的覆盖轴上，可能出现空缺的点一定在i-1的前缀和与\(\frac{x_i}{2}\)之间

我们证明这个结论：

我们现在不在乎i-1之前如何，我们之在乎i这个数，

设\(sum_i\)为前i个数的和，\(x_i\)为第i个数，我们按照\(x_i\)从小到大排序

如果在\(sum_{i-1}\)和\(\frac{x_i}{2}\)之间出现了没有覆盖的点，

因为后面的点都比\(x_i\)大，所以没有点可以填补这个空缺

还要证明\(\frac{x_i}{2}-sum_i\)这个区间是连续的

首先\(sum_i=sum_{i-1}+x_i\)那么\(\frac{sum_i}{2}\le\max(x_i,sum_{i-1})\)

所以这样的区间一定可以接上。

AC_code

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
const int N=1e5+5;
ll n,a[N],sum[N],rec;
signed main(){
	scanf("%lld",&n);
	for(re i=1;i<=n;i++)scanf("%lld",&a[i]);
	sort(a+1,a+n+1);
	for(re i=1;i<=n;i++){
		rec+=((a[i]+1)/2-sum[i-1]-1>0?(a[i]+1)/2-sum[i-1]-1:0);
		sum[i]=sum[i-1]+a[i];
	}
	printf("%lld",sum[n]-rec);
}

T4 ants

题面翻译：给定l,r，求[l,r]区间内的数的最长连续段

回滚莫队大板子。。。

AC_code

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=100005;
int n,m;
int c[N],pos[N],di;
int ans[N];
int lb[N],rb[N];
struct query{
	int l,r,id,p;
}qus[N];
struct front{
	int typ,p,val;
}fro[N];
inline bool comp(query x,query y){
	if(pos[x.l]==pos[y.l])
		return x.r<y.r;
	return x.l<y.l;
}
int main(){
	scanf("%d%d",&n,&m);
	di=sqrt(n);
	for(re i=1;i<=n;i++){
		scanf("%d",&c[i]);
		pos[i]=i/di+1;
	}
	for(re i=1;i<=m;i++){
		scanf("%d%d",&qus[i].l,&qus[i].r);
		qus[i].id=i;
		qus[i].p=pos[qus[i].l];
	}
	sort(qus+1,qus+m+1,comp);
	int r,sum,res,tmp;
	for(re i=1;i<=m;i++){
		if(qus[i].p!=qus[i-1].p){
			sum=0;
			for(re j=1;j<=n;j++)
				lb[j]=rb[j]=0;
			r=qus[i].p*di;
		}
		while(r<qus[i].r){
			r++;
			lb[c[r]]=lb[c[r]-1]+1;
			rb[c[r]]=rb[c[r]+1]+1;
			tmp=lb[c[r]]+rb[c[r]]-1;
			sum=max(sum,tmp);
			lb[c[r]+rb[c[r]]-1]=tmp;
			rb[c[r]-lb[c[r]]+1]=tmp;
		}
		res=sum;
		int s=0;
		for(re l=qus[i].l;l<=min(qus[i].r,qus[i].p*di);l++){
			lb[c[l]]=lb[c[l]-1]+1;
			rb[c[l]]=rb[c[l]+1]+1;
			tmp=lb[c[l]]+rb[c[l]]-1;
			res=max(res,tmp);
			fro[++s].typ=1;fro[s].p=c[l]+rb[c[l]]-1;fro[s].val=lb[c[l]+rb[c[l]]-1];
			fro[++s].typ=2;fro[s].p=c[l]-lb[c[l]]+1;fro[s].val=rb[c[l]-lb[c[l]]+1];
			lb[c[l]+rb[c[l]]-1]=tmp;
			rb[c[l]-lb[c[l]]+1]=tmp;
		}
		ans[qus[i].id]=res;
		for(re j=s;j>=1;j--){
			if(fro[j].typ==1)
				lb[fro[j].p]=fro[j].val;
			else
				rb[fro[j].p]=fro[j].val;
		}
		for(re j=qus[i].l;j<=min(qus[i].r,qus[i].p*di);j++){
			lb[c[j]]=rb[c[j]]=0;
		}
	}
	for(re i=1;i<=m;i++){
		printf("%d\n",ans[i]);
	}
}