对Spring IOC容器的思考

　　最近在看Spring5的视频教学，学到了IOC容器这块，对IOC有些浅薄的理解，分享一二；有错误之处，还请大佬指出

　　IOC（Inversion of Control 控制反转），是面向对象编程中的一种设计原则，可以用来减低计算机代码之间的耦合度。什么叫降低耦合度，大致理解就是在对代码进行维护升级的时候，尽量不去动源代码，而是采用其它方式来进行功能实现，而最常用的就是利用DI（Dependency Injection 依赖注入），通过更改配置文件的方式，来进行升级维护

　　在讨论IOC容器之前，我们要思考，为什么我们要解耦，先来个例子：

　　　　我们每天所使用的手机可以理解为一个Phone类实例，其中它有很多组成部分来构成，比如CPU、屏幕、喇叭等等。。。这些基础的元素就是类中的一个个属性，我们也可以称之为手机的依赖，DI（依赖注入）你就可以理解为一个给属性赋值的动作。然后具体的属性比如屏幕，它又属于Screen类的一个实例，它也有自己的一些属性，比如玻璃、屏幕中间的传感器等等。这样从大到小，每个类由好多属性构成，每个属性又是一个类实例，又继续分下去，可以想象当我们要造一个最新的IPhone 13手机的时候，要为每个基础属性赋值（注入依赖），不断的new实例（比如new Glass()），然后将实例作为上一层类的属性注入，然后再重复封装，直到最后组装成为一个IPhone 13手机，这时候我们才造好了一个手机。如果我们还要造另外的手机IPhone 13Pro，那么我们又要对代码进行大规模的改动。牵一发（制造另外的手机）而动全身（更改手机的基本属性）

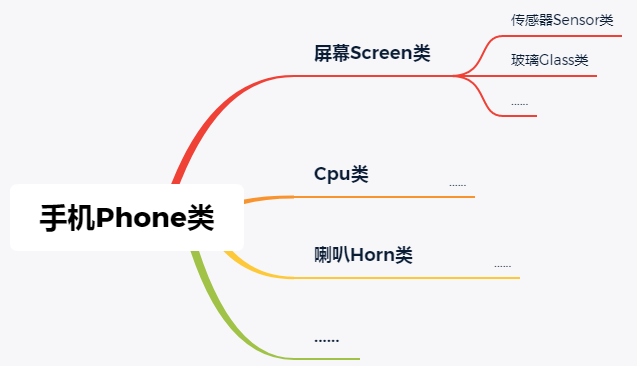
在实际的开发过程中，其实也是在各种类实例、基本数据类型作为类的属性，这将是一个巨大的工程，没人敢这么玩。

　　因此这时候，我们就需要解耦，怎么解呢？这就涉及到了今天的主题：IOC容器。

　　IOC容器是干嘛的呢，它其实就是解决了在实际开发过程中不用new的方式来造对象，而最常用的就是采用DI注入依赖（DI后面马上会重新写一个博客再说说我的看法），最常用的就是按配置文件来进行注入，通过DI利用反射+工厂模式，来动态的帮我们造对象，省去了上面说所的手动new的工程，在实际开发中，我们只需要对修改配置文件（DI需要用到的），就可以完成功能的升级、完善。这样，底层源代码还是底层源代码，不需要去改动，所要做的事就只是改我们的配置文件。