Insertion Sort and Merge Sort
Insertion Sort(插入排序)
思路:for 循环遍历数组中的每一个数
用while将每次遍历到的数于左侧的数进行对比,将小的排到左边
void InsertionSort(int*A, int n){
int key,i=0,p;
for(p=0;p<n;p++){
key=A[p];
i=p-1;
while(i>=0 && A[i]>key){
A[i+1]=A[i];
i=i-1;
}
A[i+1]=key;
}
}
中规中矩的排序方法
时间复杂度:
Best-case Running time : O(n)(数组已经被排好序的情况)
Worst-case Running Time : O(n^2)
Average Running Time : O(n^2)
从时间复杂度来看,处理少量数据还可以。当数据量较为庞大时,速度就很慢了
Merge Sort
思路:利用递归将数组分成两个相同大小的部分,直至长度为1
然后利用merge函数分别对每个部分进行排序
最后重新放在一起
void Merge(long int*A,long int left,long int center,long int right){
long int i1=left,i2=center+1,i=0,j;
long int B[100000];
long int length =sizeof(B)/sizeof(B[0]);
//比较左右两侧的大小,然后将小的的放入数组B
while (i1<=center && i2<=right)
{
if(A[i1]>A[i2]){
B[i++]=A[i2++];
}else{
B[i++]=A[i1++];
}
}
//将左侧或者右侧剩余的数以此放入数组B中
for(;i1<=center;i1++){
B[i++]=A[i1];
}
for(;i2<=right;i2++){
B[i++]=A[i2];
}
//将数组B中排好序的值赋给A
//由于每调用一次函数,B数组都会重新创建,因此B从0开始,A从left开始
for(j=0,i=left;j<=right-left;j++,i++){
A[i]=B[j];
}
}
void MergerSort(long int*A,long int left,long int right){
long int center=0;
if(left>=right){
return ;
}
center=(left+right)/2;
//这种先进行第一个递归,直至最后,没进行一次就相当于建立一层平台,当进行完后再返回上一层,执行下一个语句
MergerSort(A,left,center);
MergerSort(A,center+1,right);
Merge(A,left,center,right);
}
这个就是merge sort 的排序过程:
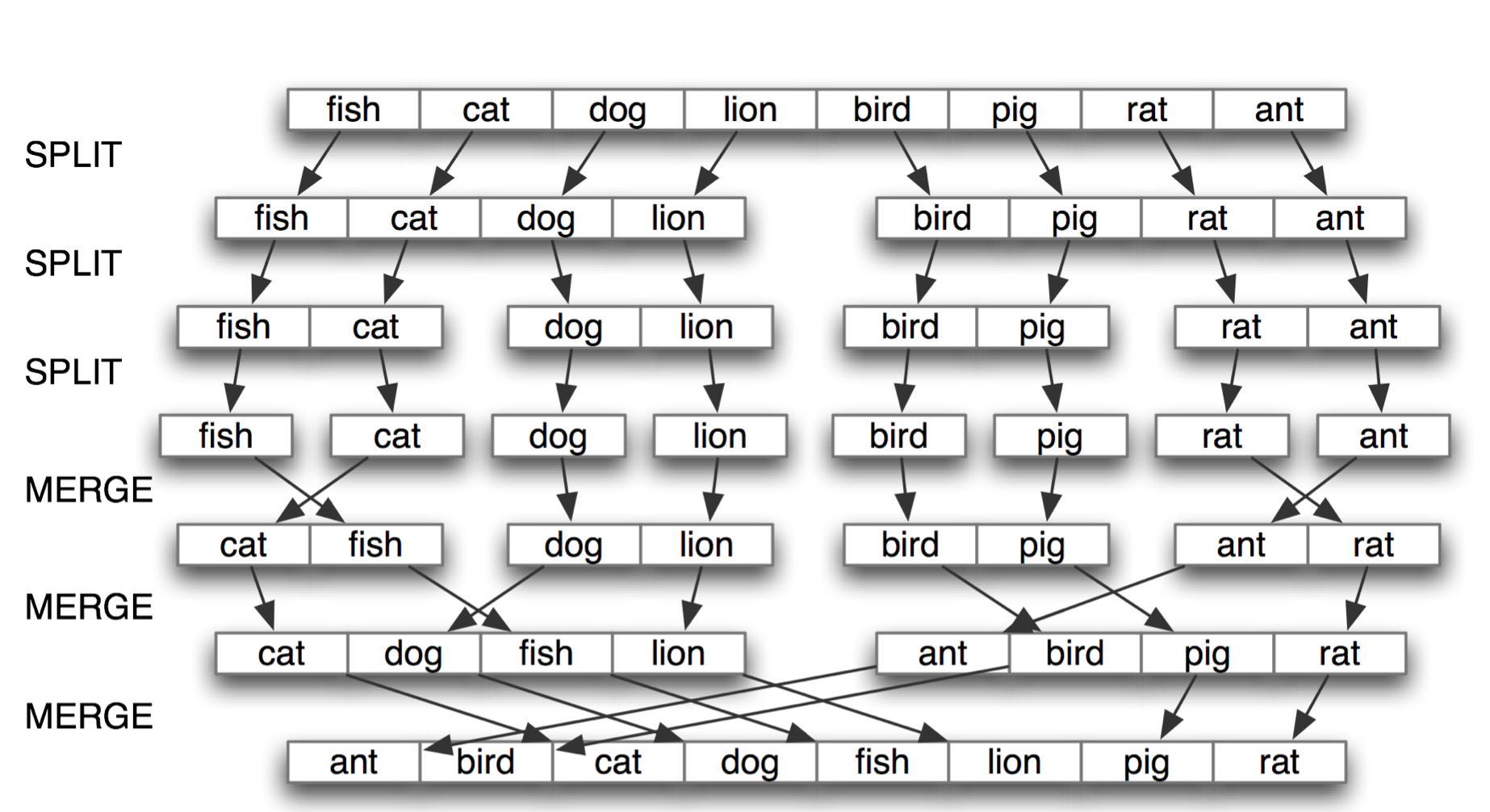
个人觉得递归部分的代码不是很好理解,其余部分都还可以
时间复杂度:
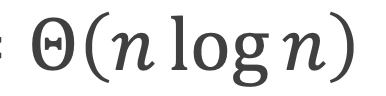
Insertion Sort and Merge Sort的更多相关文章
- Insertion Sort 与 Merge Sort的性能比较(Java)
public static void main(String[] args) { Scanner input = new Scanner(System.in); int n = input.nextI ...
- 【Sort】Merge Sort归并排序
归并排序运行时间O(N log N),但是由于需要线性附加内存,所以很少用于主存排序. 算法核心在于以下三条语句,分治递归,分别对左半边和右半边的数组进行排序,然后把左右半边的数组一一进行比较放入数组 ...
- [Algorithms] Sorting Algorithms (Insertion Sort, Bubble Sort, Merge Sort and Quicksort)
Recently I systematicall review some sorting algorithms, including insertion sort, bubble sort, merg ...
- 归并排序(merge sort)
M erge sort is based on the divide-and-conquer paradigm. Its worst-case running time has a lower ord ...
- [算法]——归并排序(Merge Sort)
归并排序(Merge Sort)与快速排序思想类似:将待排序数据分成两部分,继续将两个子部分进行递归的归并排序:然后将已经有序的两个子部分进行合并,最终完成排序.其时间复杂度与快速排序均为O(nlog ...
- SQL Tuning 基础概述06 - 表的关联方式:Nested Loops Join,Merge Sort Join & Hash Join
nested loops join(嵌套循环) 驱动表返回几条结果集,被驱动表访问多少次,有驱动顺序,无须排序,无任何限制. 驱动表限制条件有索引,被驱动表连接条件有索引. hints:use_n ...
- 归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用.将已有序的子序列合并,得到完全有序的序列:即先使每个子序列有序,再使子序 ...
- Summary: Merge Sort of Array && 求逆序对
常用算法(后面有inplace版本): package ArrayMergeSort; import java.util.Arrays; public class Solution { public ...
- 基础排序算法之并归排序(Merge Sort)
并归排序是学习分治法 (Merge Sort) 的好例子.而且它相对于选择,插入,冒泡排序来说,算法性能有一定提升.我首先会描述要解决的问题,并给出一个并归排序的例子.之后是算法的思路以及给出伪代码. ...
随机推荐
- SpringBoot 整合 hibernate 连接 Mysql 数据库
前一篇搭建了一个简易的 SpringBoot Web 项目,最重要的一步连接数据库执行增删改查命令! 经过了一天的摸爬滚打,终于成功返回数据! 因为原来项目使用的 SpringMVC + Hibern ...
- 详细探秘Linux 和 Window 双系统访问Windows 磁盘需要输入密码问题解决过程分析
将要讲很多的内容真正产生作用的配置就只有下面这一句而已.如果你只是想要解决问题看这一句就行了,后面都没有必要在看下去了. 将allow-active标签中的auth_admin_keep 改为 yes ...
- 使用PowerDesigner进行数据库设计并直接把设计好的表导出相应的建表语句
Power Designer:数据库表设计工具 PowerDesigner是Sybase公司的一款软件,使用它可以方便地对系统进行分析设计,他几乎包括了数据库模型设计的全过程.利用PowerDesig ...
- Linux的启动过程及init进程
Linux下有三个特殊进程: idle进程(pid=0)idle进程其前身是系统创建的第一个进程,0号进程,也唯一一个没有通过fork()或者kernel_thread产生的进程,由系统自动创建,运行 ...
- 在16G笔记本上安装GaussDB 200
云主机太贵(最便宜的每月几千吧),长期如果需要GaussDB200有个功能测试或学习环境,那么性价比最高的方式还是在自己的笔记本电脑上尝试安装一个本地的数据库进行学习和功能验证. 01 安装环境信息 ...
- 后端程序员之路 31、Protocol Buffer
google/protobuf: Protocol Buffers - Google's data interchange formathttps://github.com/google/protob ...
- 关于redis缓存数据库的一些思考
今晚无聊,躺在床上,在刷技术文章时,看见了一篇关于redis缓存的文章 写的蛮好,这也就引起了我对于redis思考! 不如往深了说 引起了我对于追求探索技术本质的一些思考 平时在网上刷到很多关于red ...
- AmazonS3 使用AWS SDK for Java实现跨源资源共享 (CORS)
CORS 配置 创建 CORS 配置并对存储桶设置该配置 通过添加规则来检索并修改配置 向存储桶添加修改过的配置 删除配置 import com.amazonaws.AmazonServiceExce ...
- win8 下删除服务
1.右键 我的电脑-管理-服务和应用程序-服务,找到想要删除的服务,双击后复制服务名称. 2.管理员身份运行cmd 在命令框中输入 sc delete "secbizsrv" 就删 ...
- 学习Python的书籍——入门到进阶
入门读物 <Python基础教程>(Beginning Python From Novice to Professional) <Python学习手册>(Learning Py ...
