hdu4421-Bit Magic（2-SAT）

题意

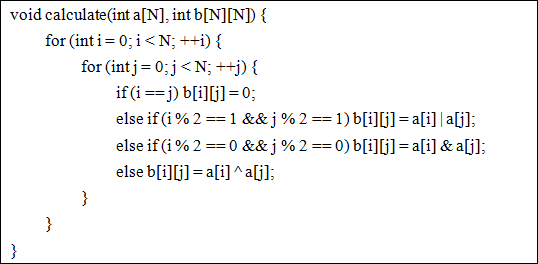
根据图中公式由A[]构造B[][]，现在给你B，问你存不存在一个数组A使之成立。

题解：对于每一位进行2-sat求解。

比赛半个小时时间，没做出来……

一直T。

因为本身对算法不确定，所以也不知道怎么办

赛后才发现是数组开小了、、、、

真坑啊。。。

#include <bits/stdc++.h>

using namespace std;

const int N = ;
int a[N], b[N][N];

struct Edge {
    int from, to, next;
} edge[N*N*];
int head[N], cntE;

void addedge(int u, int v) {
    edge[cntE].from = u;
    edge[cntE].to = v;
    edge[cntE].next = head[u];
    head[u] = cntE++;
}

int dfn[N], low[N], idx;
int stk[N], top;
int in[N];
int kind[N], cnt;

void tarjan(int u) {
    dfn[u] = low[u] = ++idx;
    in[u] = true;
    stk[++top] = u;
    for (int i = head[u]; ~i; i = edge[i].next) {
        int v = edge[i].to;
        if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
        else if (in[v]) low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++cnt;
        while () {
            int v = stk[top--];
            kind[v] = cnt;
            in[v] = false;
            if (v == u) break;
        }
    }
}

int opp[N], ind[N], col[N];
bool topsort(int n) {
    for (int i = ; i < *n; ++i) {
        if (!dfn[i]) tarjan(i);
    }
    for (int i = ; i < n; ++i) {
        int k1 = kind[i], k2 = kind[i+n];
        if (k1 == k2) return false;
    }
    return true;
}

void init() {
    cntE = ;
    memset(head, -, sizeof head);
    memset(dfn, , sizeof dfn);
    memset(in, false, sizeof in);
    idx = top = cnt = ;
    memset(ind, , sizeof ind);
    memset(col, , sizeof col);
}

int main()
{
    //freopen("in.txt", "r", stdin);

    int n;
    while (~scanf("%d", &n)) {
        for (int i = ; i < n; ++i) {
            for (int j = ; j < n; ++j) {
                scanf("%d", &b[i][j]);
            }
        }

        bool fg = true;

        for (int i = ; i < n; ++i) {
            for (int j = i; j < n; ++j) {
                if (i == j) {
                    if (b[i][j] != ) {
                        fg = false;
                        break;
                    }
                } else if (b[i][j] != b[j][i]) {
                    fg = false;
                    break;
                }
            }
            if (!fg) break;
        }

        if (!fg) {
            printf("NO\n");
            continue;
        }

        for (int w = ; w <= ; ++w) {
            init();
            int cnt = ;
            for (int i = ; i < n; ++i) {
                for (int j = i+; j < n; ++j) {
                    //if (i == j) continue;

                        if (i %  ==  && j %  == ) {
                            if (b[i][j] & ( << w)) {
                                addedge(i, i+n);
                                addedge(j, j+n);
                            } else {
                                addedge(j+n, i);
                                addedge(i+n, j);
                            }
                        } else if (i %  ==  && j %  == ) {
                            if (b[i][j] & ( << w)) {
                                addedge(j, i+n);
                                addedge(i, j+n);
                            } else {
                                addedge(i+n, i);
                                addedge(j+n, j);
                            }
                        } else {
                            if (b[i][j] & ( << w)) {
                                addedge(i, j+n);
                                addedge(j, i+n);
                                addedge(j+n, i);
                                addedge(i+n, j);
                            } else {
                                addedge(i, j);
                                addedge(j, i);
                                addedge(i+n, j+n);
                                addedge(j+n, i+n);
                            }
                        }
                }
            }
             if (!topsort(n)) {
                fg = false;
                break;
            }
        }

        if (fg) printf("YES\n");
        else printf("NO\n");
    }
    return ;
}