Topic Model

Topic Model

标签（空格分隔）： 机器学习

---

\(\Gamma\)函数

\(\Gamma\)函数可以看做是阶乘在实数域上的推广，即：
\(\Gamma(x) = \int_{0}^{+\infty} t^{x-1}e^{-t}dt = (x-1)!\)
性质：\(\frac{\Gamma(x)}{\Gamma(x-1)} = x-1\)

Beta分布

• Beta分布的概率密度：\[f(x) = \begin{cases} \frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1}, & \text{$x \in [0,1]$} \\ 0, & \text{others} \end{cases}\]
  其中，B为\(\int_{0}^{1}x^{\alpha-1}(1-x)^{\beta-1}dx = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\)；
• Beta分布的期望：\(E(x) = \int_{0}^{1}x·f(x)dx = \int_{0}^{1}x·\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}dx = \frac{\alpha}{\alpha+\beta}\)

共轭先验分布

在贝叶斯决策中，已知先验概率和似然函数，求后验概率，则可以根据贝叶斯公式求得：
\(P(\theta|x) = \frac{P(x|\theta)P(\theta)}{P(x)} \propto P(x|\theta)P(\theta)\)
而如果后验概率\(P(\theta|x)\)和先验概率P(\(\theta\))满足同样的分布律，那么，先验分布和后验分布叫做共轭分布，此时，先验分布叫做似然函数的共轭先验分布。
（当变量x是离散的时候叫做分布律，连续的时候叫做概率密度）

伯努利分布的共轭先验是Beta分布

• 伯努利分布的似然：\(P(x|\theta) = \theta^{x}(1-\theta)^{1-x}\);
• 先验函数为：\(P(\theta|\alpha, \beta) = \frac{1}{B(\alpha,\beta)}\theta^{\alpha-1}(1-\th eta)^{\beta-1}\);
• 则后验概率为：\(P(\theta|x) \propto P(x|\theta)P(\theta) \propto \theta^{(x+a)-1}(1-\theta)^{(1-x+\beta)-1}\)
  后验概率的形式与先验概率的形式是一样的，所以伯努利分布的共轭先验是Beta分布。

从Beta分布Dirichlet分布

从2到K，

• 二项分布推到多项分布；

• Beta分布推到Dirichlet分布。

• Beta分布的概率密度：\[f(x) = \begin{cases} \frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1}, & \text{$x \in [0,1]$} \\ 0, & \text{others} \end{cases}\]
  其中，\(B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\)；

• Dirichlet分布的概率密度：\[f(p|\alpha) = \begin{cases} \frac{1}{\Delta(\alpha)}\Pi_{k=1}^{K}p_{k}^{\alpha_{k}-1}, & \text{$p_{k}\in [0, 1]$} \\ 0, & \text{others} \end{cases}\]
  其中，\(\Delta(\alpha) = \frac{\Pi_{k=1}^{K}\Gamma(\alpha_{k})}{\Gamma(\sum_{k=1}^{K}\alpha_{k})}\)

对称的Dirichlet分布

即参数\(\alpha_{i}\)的值都是相等的。

• 当\(\alpha = 1\)时，退化为均匀分布；
• 当\(\alpha > 1\)时，\(p1 = p2 = p3 = ... = pk\)的概率增大；

• 当\(\alpha < 1\)时，\(pi = 1, p_{非i} = 0\)的概率增大

• 在狄利克雷分布中，\(\alpha_{i}\)是参数，那么参数\(\alpha_{i}\)对分布有什么影响呢？
  
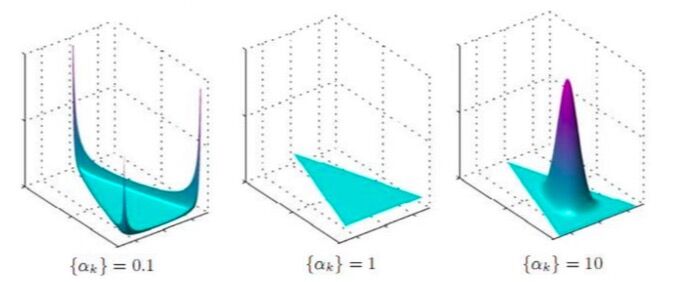
• 当\(\alpha_{k} < 1\)时，即所有的参数都取k，小于1，当某个变量趋于0时，分布会取到最大值；
• 当\(\alpha_{k} = 1\)时，即所有的参数都取1时，分布趋于均匀分布；

• 当\(\alpha_{k} > 1\)时，即所有的参数都取k，大于1，当自变量取值都相等时，分布会取到最大值。

LDA解释 —— 贝叶斯学派的典型应用

LDA是典型的无监督学习，事先不需要知道label，也不需要知道每个topic具体是什么含义，只需给出topic的数目即可。
Topic Model与聚类、降维的关系。

• Topic Model可以看做是聚类，即若干个文档在K个话题下的软聚类；

• Topic Model也可以看做是降维，由原来维度较高的次分布变为维度较低的主题分布，大大降低了特征向量的维度。
  为什么使用多话题呢？
  -- 如果语料中存在一词多义和多词一义的问题，如果使用词向量作为文档的特征，一词多义和多词一义会造成基三文档间相似度的不准确性。
  -- 所以通过增加主题的方式解决上述问题。一个词可能被映射到多个主题中，多个词可能被映射到某个主题的概率很高。

• 共有m篇文档，K个主题；
• 每篇文章（长度为N）都有各自的主题分布（多项分布），该多项分布的参数服从Dirichlet分布，参数为为\(\alpha\)；
• 每个主题都有各自的词分布（多项分布），该多项分布的参数服从Dirichlet分布，参数为\(\beta\)；

• 对于每篇文章中的第n个词，首先从该文章的主题分布中采样一个主题，然后在这个主题对应的词分布中采样一个词。不断的重塑这个随机生成过程，直到m篇文章全部完成上述过程。
  LDA的概率图模型为：
  

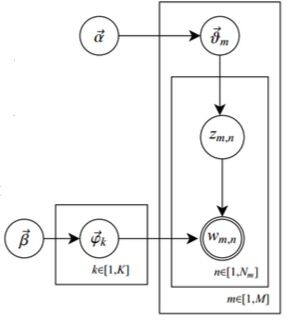
• 其中，\(\alpha\)和\(\beta\)为先验分布的参数，一般是需要事先给定，比如取0.1的堆成Dirichlet分布，表示在参数学习结束之后，期望每个文档的主题不会十分集中；
• \(\theta\)是每篇文档的主题分布，是长度为K的向量；
• \(\varphi_{k}\)表示第k个主题的词分布；

• 由\(z_{ij}\)选择\(\varphi_{zij}\)，表示由词分布\(\varphi_{zij}\)确定term，即得到观测值\(w_{ij}\)。

参数的学习

给定一个文档集合，\(w_{m,n}\)是可以观察到的已知变量，\(\alpha\)和\(\beta\)是根据经验给定的先验参数，其他的变量\(z_{m,n},\theta, \varphi\)都是未知的隐变量，需要根据观察到的变量来学习估计。则LDA所有变量的联合分布为：
\(p(w_{m}, z_{m}, \theta_{m}, \Phi|\alpha, \beta) = \Pi_{n=1}^{N_{m}}p(w_{m,n}|\varphi_{z_{m,n}})p(z_{m,n}|\theta_{m})p(\theta_{m}|\alpha)p(\Phi|\beta)\)

Gibbs Sampling

吉布斯采样算法的运行方式是每次选取概率向量的一个维度，给定其他维度的变量值采样当前维度的值。不断迭代直到收敛输出待估计的参数。

• 初始时随机给文本中的每个词分配主题\(z^{(0)}\)，然后统计每个主题z下出现词t的数量以及每个文档m下出现主题z的数量，每一轮计算\(p(z_{i}|z_{-i},d,w)\)，即排除当前词的主题分布；
• 根据其他所有词的主题分布估计当前词分配各个主题的概率；
• 当得到当前词属于所有主题z的概率分布后，根据这个概率分布为该词采样一个新的主题；
• 用同样的方法更新下一个词的主题，直到发现每个文档的主题分布\(\theta_{i}\)和每个主题的词分布\(\varphi_{i}\)收敛。算法停止，输出待估计的参数\(\theta\)和\(\varphi\)，同时每个单词的主题也可以得出