特征值分解与奇异值分解(SVD)

1.使用QR分解获取特征值和特征向量

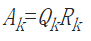
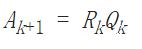
将矩阵A进行QR分解，得到正规正交矩阵Q与上三角形矩阵R。由上可知Ak为相似矩阵，当k增加时，Ak收敛到上三角矩阵，特征值为对角项。

2.奇异值分解(SVD)

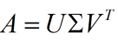
其中U是m×m阶酉矩阵；Σ是半正定m×n阶对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。

将矩阵A乘它的转置，得到的方阵可用于求特征向量v，进而求出奇异值σ和左奇异向量u。

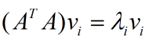
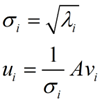
 #coding:utf8
 import numpy as np
 np.set_printoptions(precision=4, suppress=True)
 
 def householder_reflection(A):
     """Householder变换"""
     (r, c) = np.shape(A)
     Q = np.identity(r)
     R = np.copy(A)
     for cnt in range(r - 1):
         x = R[cnt:, cnt]
         e = np.zeros_like(x)
         e[0] = np.linalg.norm(x)
         u = x - e
         v = u / np.linalg.norm(u)
         Q_cnt = np.identity(r)
         Q_cnt[cnt:, cnt:] -= 2.0 * np.outer(v, v)
         R = np.dot(Q_cnt, R)  # R=H(n-1)*...*H(2)*H(1)*A
         Q = np.dot(Q, Q_cnt)  # Q=H(n-1)*...*H(2)*H(1)  H为自逆矩阵
     return (Q, R)
 
 def eig(A, epsilon=1e-10):
     '''采用QR分解法计算特征值和特征向量 '''
     (q,r_)=householder_reflection(A)
     h = np.identity(A.shape[0])
     for i in range(50):
         B=np.dot(r_,q)
         h=h.dot(q)
         (q,r)=gram_schmidt(B)
         if abs(r.trace()-r_.trace())< epsilon:
             print("Converged in {} iterations!".format(i))
             break
         r_=r
     return r,h
 
 def svd(A):
     '''奇异值分解'''
     n, m = A.shape
     svd_ = []
     k = min(n, m)
     v_=eig(np.dot(A.T, A))[1]  #np.linalg.eig(np.dot(A.T, A))[1]
     for i in range(k):
         v=v_.T[i]
         u_ = np.dot(A, v)
         s = np.linalg.norm(u_)
         u = u_ / s
         svd_.append((s, u, v))
     ss, us, vs = [np.array(x) for x in zip(*svd_)]
     return  us.T,ss, vs
 
 if __name__ == "__main__":
 
     mat = np.array([
         [2, 5, 3],
         [1, 2, 1],
         [4, 1, 1],
         [3, 5, 2],
         [5, 3, 1],
         [4, 5, 5],
         [2, 4, 2],
         [2, 2, 5],
     ], dtype='float64')
     u,s,v = svd(mat)
     print u
     print s
     print v
     print np.dot(np.dot(u,np.diag(s)),v)