凸优化: 回溯线搜索(Backtracking line search)
声明:
本文大量摘录 https://www.cnblogs.com/kemaswill/p/3416231.html 内容。
======================================
回溯线搜索(Backtracking line search)
预备知识:
函数的梯度--最快上升方向。下降方向则是负梯度。
给出 回溯线搜索(Backtracking line search)的算法流程描述:

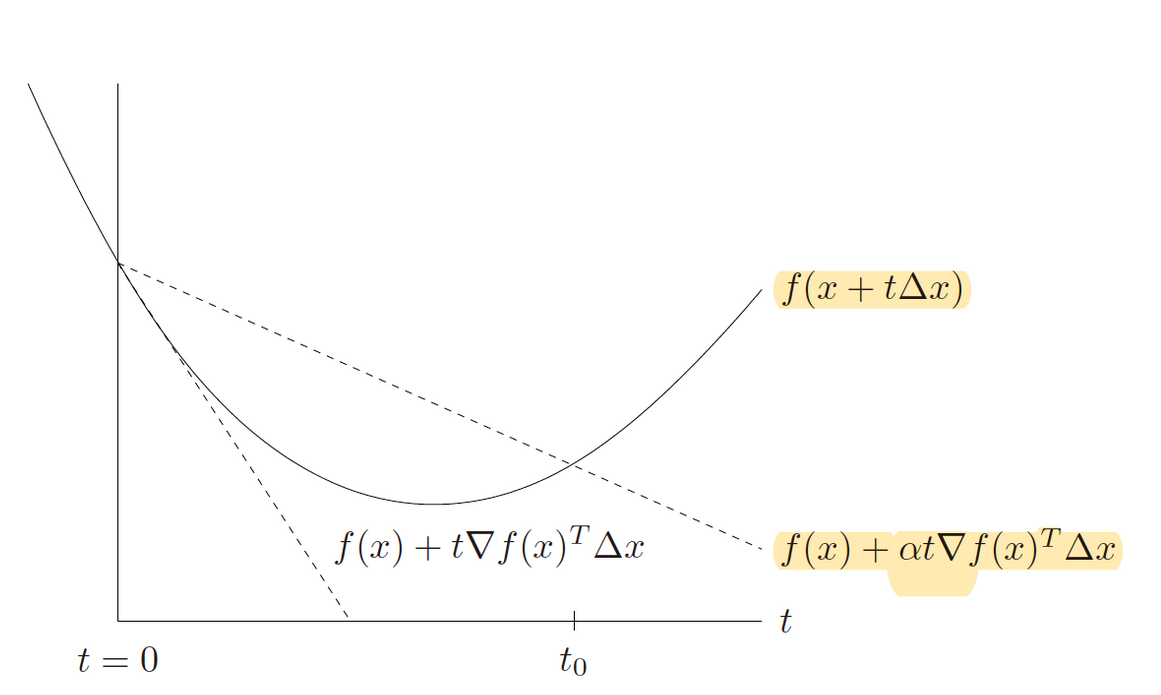
===================================================
下面内容摘录自:
https://www.cnblogs.com/kemaswill/p/3416231.html
个人推荐阅读上面这个链接的内容,这个内容比较易懂,而且讲的也比较透彻。

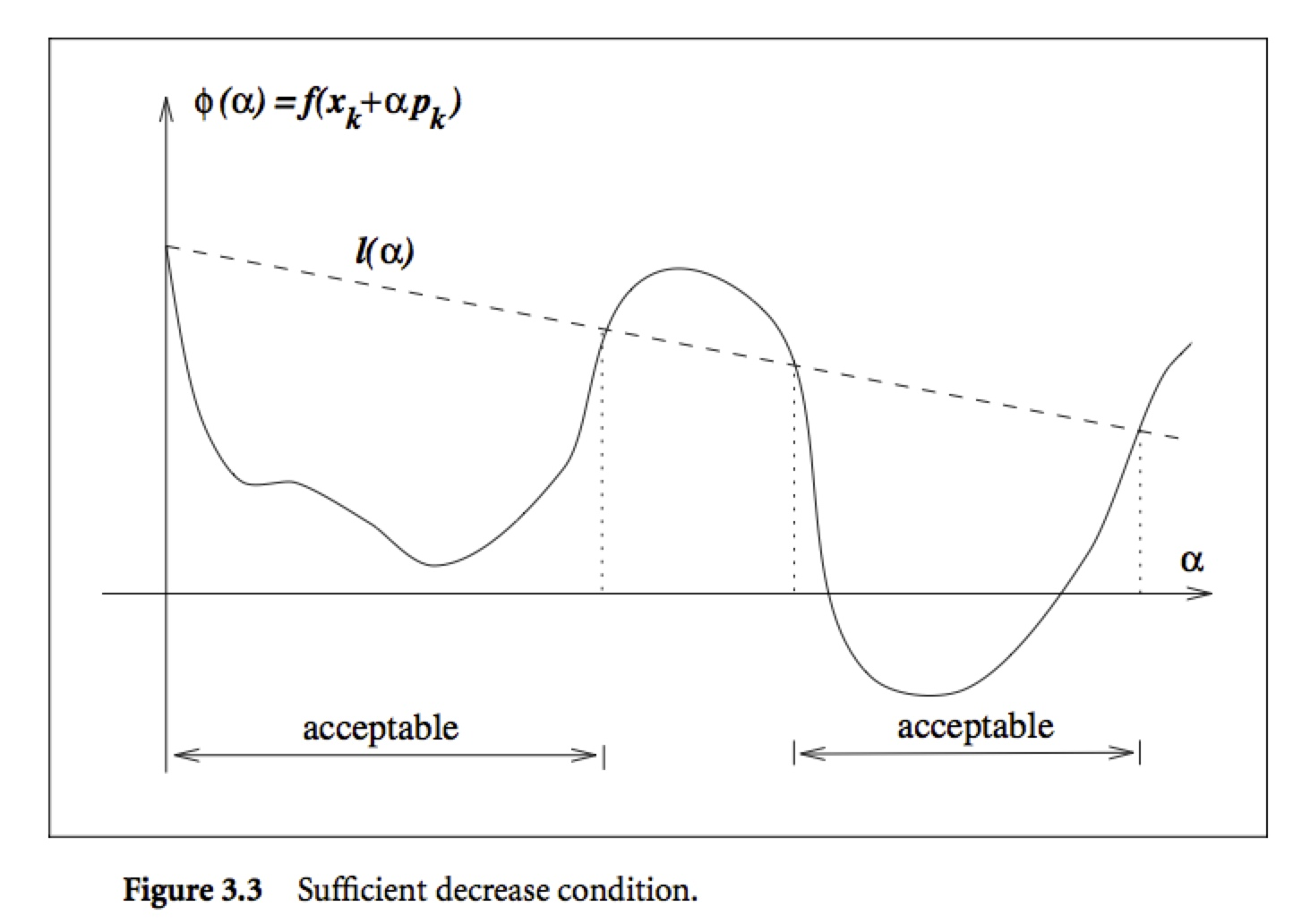

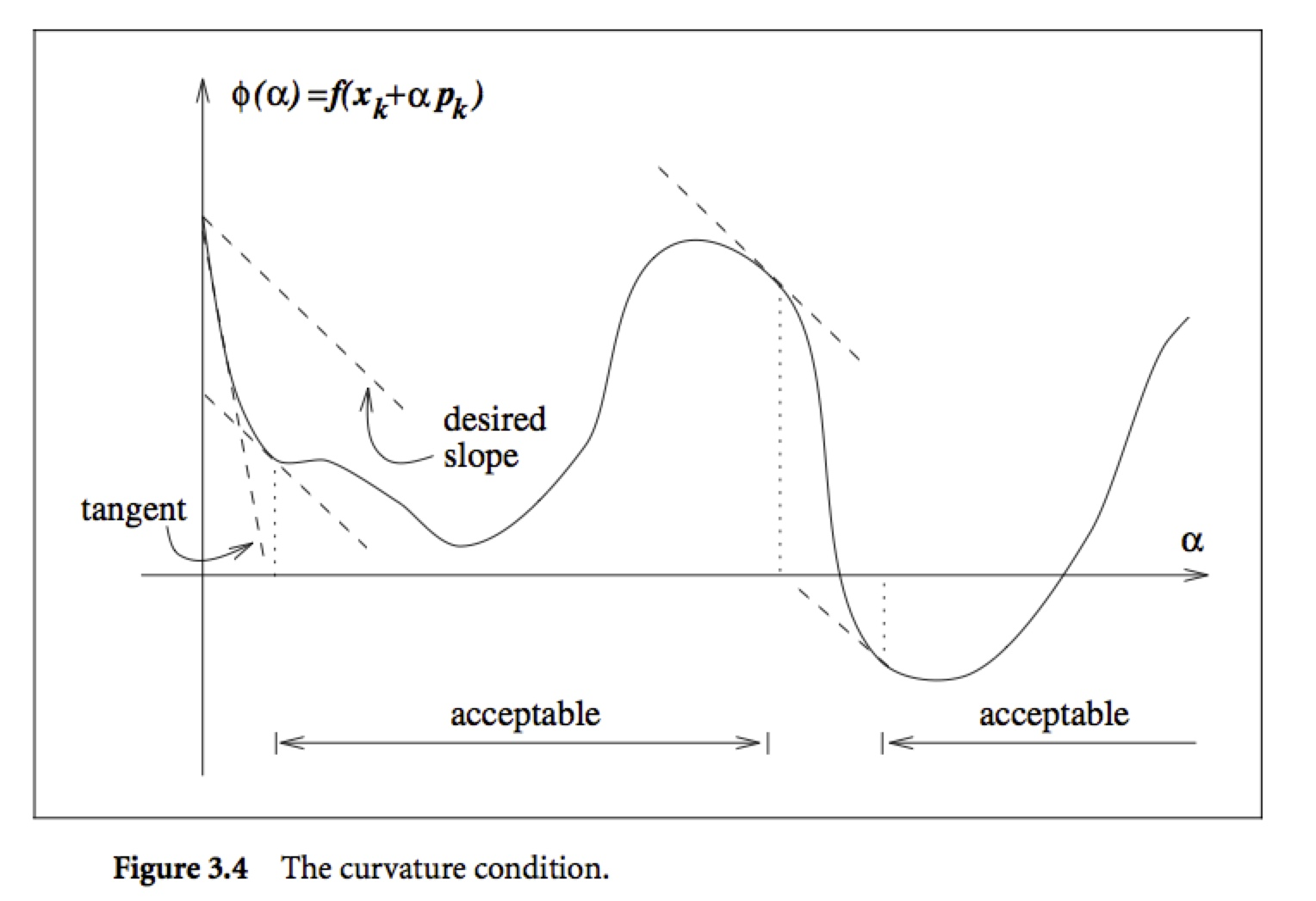

===================================================
根据 https://www.cnblogs.com/kemaswill/p/3416231.html 中的理论,我们可以得到下面的demo代码:
import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.25
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
data_gen = Data_Gen(N)
x = torch.randn(N, requires_grad=True) #####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
sgd(x, data_gen) # bls算法
bls(x, data_gen) #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
"""
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
sgd(x, data_gen) # bls算法
bls(x, data_gen)
"""
对于二阶正定矩阵所形成的凸优化问题,我们使用随机梯度下降,代码:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.25
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
data_gen = Data_Gen(N)
x = torch.randn(N, requires_grad=True) #####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
sgd(x, data_gen) # bls算法
# bls(x, data_gen) #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
"""
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
sgd(x, data_gen) # bls算法
bls(x, data_gen)
"""
运行结果:
iter_num: 109598 y_old: -24.1126766204834 y_new: -24.11280059814453
iter_num: 109599 y_old: -24.11280059814453 y_new: -24.11285972595215
iter_num: 109600 y_old: -24.11285972595215 y_new: -24.112972259521484
iter_num: 109601 y_old: -24.112972259521484 y_new: -24.113067626953125
iter_num: 109602 y_old: -24.113067626953125 y_new: -24.113168716430664
iter_num: 109603 y_old: -24.113168716430664 y_new: -24.113237380981445
iter_num: 109604 y_old: -24.113237380981445 y_new: -24.11332130432129
iter_num: 109605 y_old: -24.11332130432129 y_new: -24.113388061523438
iter_num: 109606 y_old: -24.113388061523438 y_new: -24.11349868774414
iter_num: 109607 y_old: -24.11349868774414 y_new: -24.11361312866211
iter_num: 109608 y_old: -24.11361312866211 y_new: -24.113622665405273
对于二阶正定矩阵所形成的凸优化问题,我们使用bls算法,代码:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.25
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
data_gen = Data_Gen(N)
x = torch.randn(N, requires_grad=True) #####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen) #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
"""
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
sgd(x, data_gen) # bls算法
bls(x, data_gen)
"""
运行结果:
iter_num: 1 search_time: 4 y_old: 741.302490234375 y_new: 61.191226959228516
iter_num: 2 search_time: 4 y_old: 61.191226959228516 y_new: -6.580791473388672
iter_num: 3 search_time: 5 y_old: -6.580791473388672 y_new: -24.848424911499023
iter_num: 4 search_time: 5 y_old: -24.848424911499023 y_new: -25.728652954101562
iter_num: 5 search_time: 5 y_old: -25.728652954101562 y_new: -25.78291893005371
iter_num: 6 search_time: 5 y_old: -25.78291893005371 y_new: -25.786640167236328
iter_num: 7 search_time: 5 y_old: -25.786640167236328 y_new: -25.786869049072266
iter_num: 8 search_time: 3 y_old: -25.786869049072266 y_new: -25.786916732788086
iter_num: 9 search_time: 5 y_old: -25.786916732788086 y_new: -25.786951065063477
iter_num: 10 search_time: 3 y_old: -25.786951065063477 y_new: -25.78696060180664
可以看到,对于凸优化问题,我们使用随机梯度下降和bls算法相差不大,甚至bls算法的结果要由于随机梯度下降,但是最为重要的是运算的迭代次数,我们可以看到随机梯度下降算法共进行了109608次迭代,而bls算法只进行了10次迭代,虽然bls算法在每次迭代的过程中都会进行search操作,但是每次迭代过程中search次数都没有超过5。
可以看到对于凸优化问题,bls算法在总体表现上要优与随机梯度sgd算法。
对于非凸优化问题,给出demo代码:
非凸优化问题,随机梯度下降算法,sgd:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.25
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
x = torch.randn(N, requires_grad=True) """
#####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
""" #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
sgd(x, data_gen) # bls算法
# bls(x, data_gen)
运算结果:
iter_num: 18261 y_old: 29.948509216308594 y_new: 29.945993423461914
iter_num: 18262 y_old: 29.945993423461914 y_new: 29.94289207458496
iter_num: 18263 y_old: 29.94289207458496 y_new: 29.940031051635742
iter_num: 18264 y_old: 29.940031051635742 y_new: 29.93958282470703
iter_num: 18265 y_old: 29.93958282470703 y_new: 29.936599731445312
iter_num: 18266 y_old: 29.936599731445312 y_new: 29.932973861694336
iter_num: 18267 y_old: 29.932973861694336 y_new: 29.930309295654297
iter_num: 18268 y_old: 29.930309295654297 y_new: 29.92643165588379
iter_num: 18269 y_old: 29.92643165588379 y_new: 29.92643928527832
非凸优化问题,bls算法,代码:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.25
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
x = torch.randn(N, requires_grad=True) """
#####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
""" #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
运算结果:
iter_num: 12931 search_time: 50 y_old: 21.942323684692383 y_new: 21.939422607421875
iter_num: 12932 search_time: 49 y_old: 21.939422607421875 y_new: 21.936918258666992
iter_num: 12933 search_time: 51 y_old: 21.936918258666992 y_new: 21.934120178222656
iter_num: 12934 search_time: 47 y_old: 21.934120178222656 y_new: 21.93170738220215
iter_num: 12935 search_time: 51 y_old: 21.93170738220215 y_new: 21.92693519592285
iter_num: 12936 search_time: 48 y_old: 21.92693519592285 y_new: 21.924362182617188
iter_num: 12937 search_time: 51 y_old: 21.924362182617188 y_new: 21.922771453857422
iter_num: 12938 search_time: 45 y_old: 21.922771453857422 y_new: 21.919511795043945
iter_num: 12939 search_time: 51 y_old: 21.919511795043945 y_new: 21.914203643798828
iter_num: 12940 search_time: 49 y_old: 21.914203643798828 y_new: 21.911758422851562
iter_num: 12941 search_time: 51 y_old: 21.911758422851562 y_new: 21.9085693359375
iter_num: 12942 search_time: 48 y_old: 21.9085693359375 y_new: 21.904415130615234
iter_num: 12943 search_time: 89 y_old: 21.904415130615234 y_new: 21.904300689697266
iter_num: 12944 search_time: 90 y_old: 21.904300689697266 y_new: 21.904294967651367
可以看到,对于非凸优化问题,bls算法虽然依旧获得由于sgd算法的结果,但是在运算迭代次数上却远远高于sgd算法;上面的非凸优化问题,随机梯度下降共迭代18296次,而bls算法迭代12944次,但是bls算法在每次迭代过程中都进行了50次左右的search,因此bls算法对于非凸优化问题在运行时间上是不占优势的。
不过对于bls算法,我们可以通过对其参数的修改优化其运算性能,比如将 c 设置为: c = 0.5
代码:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.5
beta = 0.8
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
x = torch.randn(N, requires_grad=True) """
#####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
""" #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
运算结果:
iter_num: 3676 search_time: 53 y_old: 29.511341094970703 y_new: 29.50807762145996
iter_num: 3677 search_time: 34 y_old: 29.50807762145996 y_new: 29.432992935180664
iter_num: 3678 search_time: 53 y_old: 29.432992935180664 y_new: 29.379230499267578
iter_num: 3679 search_time: 47 y_old: 29.379230499267578 y_new: 29.374101638793945
iter_num: 3680 search_time: 51 y_old: 29.374101638793945 y_new: 29.368497848510742
iter_num: 3681 search_time: 62 y_old: 29.368497848510742 y_new: 29.3680362701416
iter_num: 3682 search_time: 70 y_old: 29.3680362701416 y_new: 29.367828369140625
iter_num: 3683 search_time: 82 y_old: 29.367828369140625 y_new: 29.367551803588867
iter_num: 3684 search_time: 90 y_old: 29.367551803588867 y_new: 29.367528915405273
iter_num: 3685 search_time: 98 y_old: 29.367528915405273 y_new: 29.367528915405273
将 c 设置为: c = 0.5, 将 beta 设置为:beta=0.1
代码:


import random
import numpy as np
from scipy.linalg import orth
import torch seed = 9999
random.seed(seed)
np.random.seed(seed) torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True class Data_Gen():
def __init__(self, N, positive_definite=True):
self.N = N # 不变的矩阵
B = np.random.rand(N, 1)
# 数据集,数据B矩阵
self.B = torch.tensor(B, dtype=torch.float32) if positive_definite==True:
# 正定矩阵的生成, A_
X = np.diag(np.abs(np.random.rand(N))+1)
U = orth(np.random.rand(N, N))
A = np.dot(np.dot(U.T, X), U)
else:
# 非正定矩阵的生成,A
M = np.random.rand(N, N)
A = np.dot(M.T, M) + 0.01*np.eye(N)
self.A = torch.tensor(A, dtype=torch.float32) def data_gen(self, x: torch.FloatTensor):
""" 数据生成 """
# 训练数据,x_data, x
# x = torch.randn(N, requires_grad=True)
N = x.size()[0]
assert N==self.N, "向量长度不匹配" # 构建训练数据,非正定数据矩阵生成的y_data
y=self.object_fun(self.A, self.B, x)
return y def object_fun(self, A: torch.FloatTensor, B: torch.FloatTensor, x: torch.FloatTensor):
if x.dim() == 1:
x = torch.unsqueeze(x, 1)
ans = torch.mm(x.T, torch.mm(A, x)) + torch.mm(x.T, B)
# print( torch.mm(A, x) )
# print( torch.mm(x.T, torch.mm(A, x)) )
# print( torch.mm(x.T, B) )
return torch.squeeze(ans) #####################################################
# 随机梯度法
def sgd(x: torch.FloatTensor, data_gen: Data_Gen, step=0.00001):
# x = torch.randn(N, device="cuda:0", requires_grad=True)
y = data_gen.data_gen(x) iter_num = 0
while True:
g = torch.autograd.grad(y, x, retain_graph=False, create_graph=False)[0]
x.data.add_( -step*g )
y_new = data_gen.data_gen(x) iter_num += 1
print("iter_num: ", iter_num, "y_old: ", y.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y.item()) < 0.00001:
break
else:
y = y_new #####################################################
# 回溯线搜索(Backtracking line search)
def bls(x: torch.FloatTensor, data_gen: Data_Gen):
iter_num = 0
c = 0.5
beta = 0.1
while True:
iter_num += 1
y0 = data_gen.data_gen(x)
g = torch.autograd.grad(y0, x, retain_graph=False, create_graph=False)[0] p = -1.0*g # 求最小值,梯度下降,使用负梯度
delta_f = g search_time = 0
alpha_step = 1.0
while True:
y_new = data_gen.data_gen(x.detach() + alpha_step*p)
y_up = y0 + c*alpha_step*torch.dot(delta_f, p) if y_new.item() > y_up.item():
search_time += 1
alpha_step *= beta
else:
break
x.data.add_( alpha_step*p ) print("iter_num: ", iter_num, "search_time: ", search_time, " y_old: ", y0.item(), "y_new: ", y_new.item())
if abs(y_new.item()-y0.item()) < 0.00001:
break if __name__ == '__main__':
# 数据生成
N = 500
x = torch.randn(N, requires_grad=True) """
#####################################################
# 对凸二次函数进行求解,正定矩阵,求解最小值
#####################################################
# data_gen = Data_Gen(N) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
""" #####################################################
# 对非凸二次函数进行求解,非正定矩阵,求解最小值
#####################################################
data_gen = Data_Gen(N, positive_definite=False) # 随机梯度法
# sgd(x, data_gen) # bls算法
bls(x, data_gen)
运算结果:
iter_num: 1838 search_time: 6 y_old: 83.01563262939453 y_new: 82.85948181152344
iter_num: 1839 search_time: 6 y_old: 82.85948181152344 y_new: 82.74000549316406
iter_num: 1840 search_time: 6 y_old: 82.74000549316406 y_new: 82.64784240722656
iter_num: 1841 search_time: 6 y_old: 82.64784240722656 y_new: 82.57584381103516
iter_num: 1842 search_time: 6 y_old: 82.57584381103516 y_new: 82.52399444580078
iter_num: 1843 search_time: 6 y_old: 82.52399444580078 y_new: 82.48124694824219
iter_num: 1844 search_time: 6 y_old: 82.48124694824219 y_new: 82.44764709472656
iter_num: 1845 search_time: 6 y_old: 82.44764709472656 y_new: 82.42279815673828
iter_num: 1846 search_time: 6 y_old: 82.42279815673828 y_new: 82.40233612060547
iter_num: 1847 search_time: 6 y_old: 82.40233612060547 y_new: 82.38795471191406
iter_num: 1848 search_time: 6 y_old: 82.38795471191406 y_new: 82.37630462646484
iter_num: 1849 search_time: 6 y_old: 82.37630462646484 y_new: 82.36550903320312
iter_num: 1850 search_time: 6 y_old: 82.36550903320312 y_new: 82.35576629638672
iter_num: 1851 search_time: 11 y_old: 82.35576629638672 y_new: 82.35576629638672
可以看到,对于非凸优化问题,如果使用bls算法,在追求运算速度的情况下必然要舍弃最终的运算结果性能,而追求运算结果的性能必然要花费大量的运算时间,因此可以说bls算法更适合于凸优化问题,而对于非凸问题,bls算法往往难以得到很好的性能表现。
===================================================
参考:
https://zhuanlan.zhihu.com/p/590013413
https://blog.csdn.net/jianti9962/article/details/121739041
https://www.cnblogs.com/fstang/p/4192735.html
凸优化: 回溯线搜索(Backtracking line search)的更多相关文章
- 【原创】回溯线搜索 Backtracking line search
机器学习中很多数值优化算法都会用到线搜索(line search).线搜索的目的是在搜索方向上找到是目标函数\(f(x)\)最小的点.然而,精确找到最小点比较耗时,由于搜索方向本来就是近似,所以用较小 ...
- Backtracking line search的理解
使用梯度下降方法求解凸优化问题的时候,会遇到一个问题,选择什么样的梯度下降步长才合适. 假设优化函数为,若每次梯度下降的步长都固定,则可能出现左图所示的情况,无法收敛.若每次步长都很小,则下降速度非常 ...
- 重新发现梯度下降法--backtracking line search
一直以为梯度下降很简单的,结果最近发现我写的一个梯度下降特别慢,后来终于找到原因:step size的选择很关键,有一种叫backtracking line search的梯度下降法就非常高效,该算法 ...
- 线搜索(line search)方法
在机器学习中, 通常需要求某个函数的最值(比如最大似然中需要求的似然的最大值). 线搜索(line search)是求得一个函数\(f(x)\)的最值的两种常用迭代方法之一(另外一个是trust re ...
- Line Search and Quasi-Newton Methods 线性搜索与拟牛顿法
Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...
- Line Search and Quasi-Newton Methods
Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...
- 一段有关线搜索的从python到matlab的代码
在Udacity上很多关于机器学习的课程几乎都是基于python语言的,博主“ttang”的博文“重新发现梯度下降法——backtracking line search”里对回溯线搜索的算法实现也是用 ...
- Leetcode之回溯法专题-79. 单词搜索(Word Search)
Leetcode之回溯法专题-79. 单词搜索(Word Search) 给定一个二维网格和一个单词,找出该单词是否存在于网格中. 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元 ...
- [原创]用“人话”解释不精确线搜索中的Armijo-Goldstein准则及Wolfe-Powell准则
[原创]用“人话”解释不精确线搜索中的Armijo-Goldstein准则及Wolfe-Powell准则 转载请注明出处:http://www.codelast.com/ line search(一维 ...
- 用“人话”解释不精确线搜索中的Armijo-Goldstein准则及Wolfe-Powell准则
转载请注明出处:http://www.codelast.com/ line search(一维搜索,或线搜索)是最优化(Optimization)算法中的一个基础步骤/算法.它可以分为精确的一维搜索以 ...
随机推荐
- 夜莺中心端管理categraf采集规则并下发
痛点 市面上常见的采集器,比如 telegraf.grafana-agent.datadog-agent 等,通常内置了多种采集插件,比如可以采集操作系统的常规指标,也可以采集 mysql.redis ...
- Kubernetes监控手册06-监控APIServer
写在前面 如果是用的公有云托管的 Kubernetes 集群,控制面的组件都交由云厂商托管的,那作为客户的我们就省事了,基本不用操心 APIServer 的运维.个人也推荐使用云厂商这个服务,毕竟 K ...
- NFS练习
NFS练习题 1.开放/nfs/share目录,提供给 任意用户 只读(/etc/exports ro) 查询 1.任意客户端2.任意的用户 服务端 showmout exportfs system ...
- Promise 期约
Promise 期约之前 回调地狱 设想这样一个经常发生的场景,我们希望处理Ajax请求的结果,所以我们将处理请求结果的方法作为回调传入,需要将请求结果继续处理,这就导致我们陷入了回调地狱 doSom ...
- HTTP报文结构详解
HTTP/HTTPS简介HTTP 协议是 Hyper Text Transfer Protocol(超文本传输协议)的缩写,是用于从万维网( WWW:World Wide Web )服务器传输超文本到 ...
- flutter 创建第一个项目(二)
新建flutter project 项目 这样就创建出了第一个项目
- PI规划会,研发团队价值聚焦的一剂良方
随着数字化建设如火如荼地推进,中大型企业的数字化建设团队规模也越来越大,团队规模的扩大一方面带来了更多产能与可能性,另一方面,不同的角色在不同的业务场景也带来了一些现实问题,例如: 作为CIO 或产品 ...
- 『手撕Vue-CLI』自动安装依赖
开篇 经过『手撕Vue-CLI』拷贝模板,实现了自动下载并复制指定模板到目标目录.然而,虽然项目已复制,但其依赖并未自动安装,可能需要用户手动操作,这并不够智能. 正如前文所述,我们已经了解了业务需求 ...
- Vue 打包相关
Vue 打包相关 vue-cli-service build# 用法:vue-cli-service build [options] [entry|pattern] 选项: --mode 指定环境模式 ...
- XAF 属性编辑器(PropertyEditor)- 原理篇
前言 随着 DEV24.1.3 的发布,XAF Blazor 中的属性编辑器(PropertyEditor)也进行了很大的改动,在使用体验上也更接近 WinForm 了,由于进行了大量的封装,理解上没 ...
