TS实现汉诺塔算法，以及图灵完备讨论

之前在网上看到徐大佬更新的一篇文章：

用 TypeScript 类型运算实现一个中国象棋程序

在线预览地址：https://tsplay.dev/Nd4n0N 把鼠标放在最后几行的走棋结果上，惊喜的一幕出现了，有点发现新大陆的感觉，哇，炫酷。

后面就很好奇，是如何实现的呢？

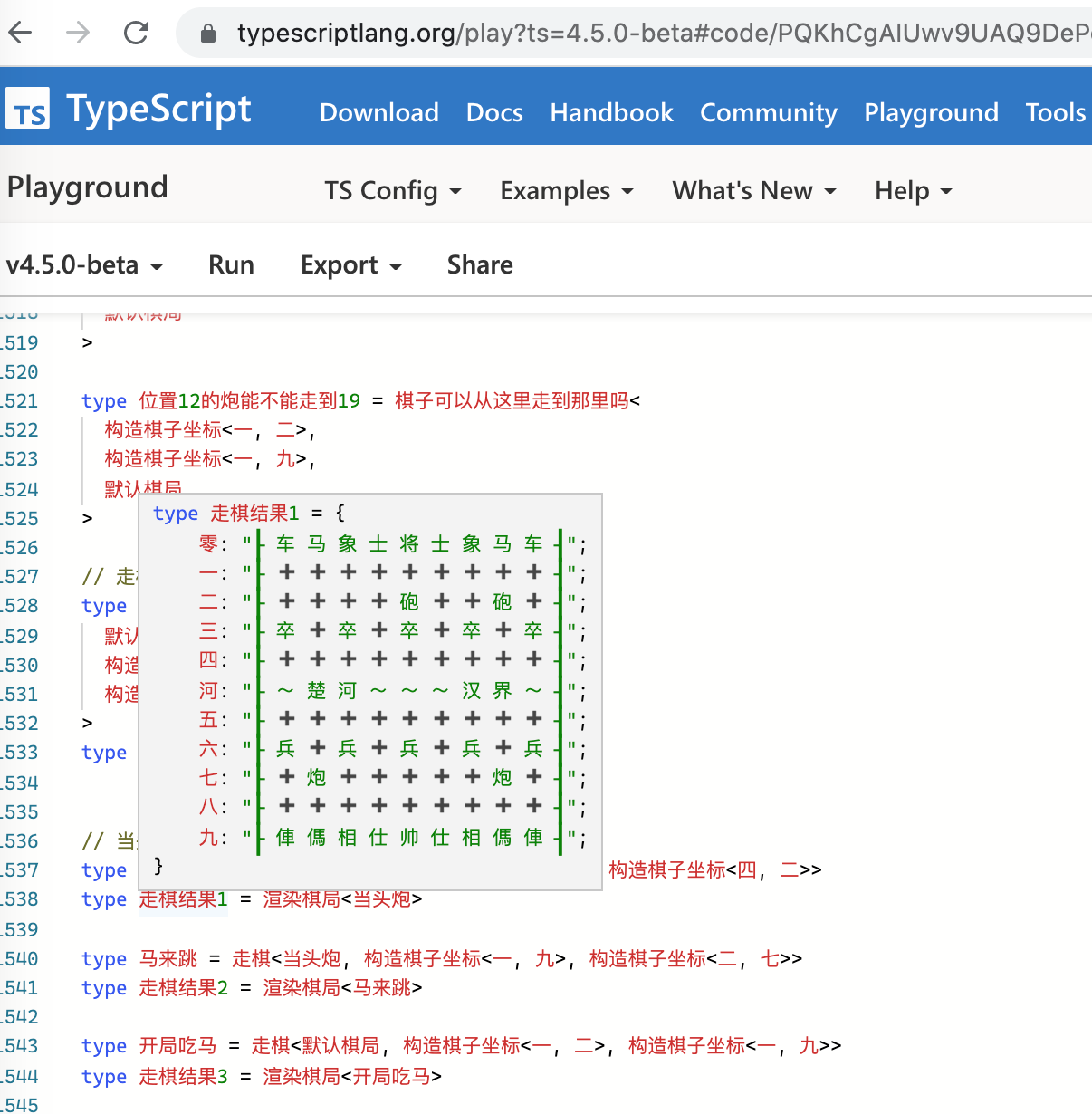
我们先看大佬说的第一句话，“众所周知，TypeScript 是图灵完备的……”为什么说ts是图灵完备的呢？下面开始了我的探索。

什么是图灵完备？

维基百科是这样定义的：

一个计算系统可以计算任何图灵-可计算函数，被称作图灵完全（或者图灵完备）。或者任何可以模拟通用图灵机的系统。

即如果一个设备可以模拟图灵机，那么它就可以执行任何种类的计算。

它意味着任何实现以下八条指令的机器都是一台计算机（因此可以执行任何种类的计算）。

• . ,: 输入或输出一个指令
• + -: 加或减内存中的值
• > <: 将当前的指针向左或向右移动。
• [ ]: 执行循环

如果某种语言可以执行以上八种指令，就可以称为是图灵完备的。

我们用以上八种指令，验证一下，狗狗是否是图灵完备的，狗狗叫小花。

1、输入/输出

我拍了拍小花的头，她看了看我，然后继续趴着。

输入：拍头

输出：抬头，趴着

完成！

2、增加/减少内存中的值

瓷砖格子很像图灵机的纸条，我把狗粮撒在瓷砖上，小花可以直接从地板吃下去，她可以吃掉，也可以吐出来。

所以她可以增加/减少内存中的值。

完成！

3、将当前记忆头指针向前或向后移动

一天，小花跟yoyo疯跑，把她的饭盒移动，狗粮撒的到处都是。

如上图，在制造这个混乱的时候，她把她的饭盒移开了。

移开她的饭盒意味着她会把她的狗粮洒在另一块瓷砖上。

这算作转移记忆头，编辑另一个记忆单元。存储指针移动啦！

完成！

4、执行循环

刚把地上打扫干净，小花一会又把地上弄乱了。

实现循环

完成！

以上，我们证明小花是图灵完备的，那如何利用她的完备性进行程序计算呢？

好吧，让小花来执行一段：

好像不行哎～

尽管她是图灵完备的，但也不是专门用来程序计算的。所以能进行程序计算的一定是图灵完备的，图灵完备的不一定能进行程序计算。

不过，既然可以实现象棋，而且是用中文写的哦，超级厉害！

那TS是可以进行计算的，我也来试试吧！

之前公众号写过python实现汉诺塔的图解递归算法，改改

//核心：每个类型可以看成一个函数，传入的泛型是函数参数，并且也是一个类型，最后再返回一个新的类型
type 塔一 = 'A'

type 塔二 = 'B'

type 塔三 = 'C'

// type 塔 = 塔一 | 塔二 | 塔三
type 得到长度<数组 extends any[]> = 数组["length"];

//exstends 和后边的 ? 构成了一个三元表达式，如果 extends 前面的类型能够赋值给 extends 后面的类型，那么表达式判断为真，否则为假。
type 转为数组<

某数 extends number,

对应数组 extends any[] = [] // 默认值赋一个空数组，外部调用的时候不需要传

> = 得到长度<对应数组> extends 某数 // 长度是否等于了需要的长度

? 对应数组 // 如果长度等于所需要的了就返回

: 转为数组<某数, [any, ...对应数组]>; // 否则再添加一个元素进入数组，然后递归调用

type 相加<某数甲 extends number, 某数乙 extends number> = 得到长度<

[...转为数组<某数甲>, ...转为数组<某数乙>]
>;

type 数组减一<某数组类型 extends any[]> = ((

...参数: 某数组类型

) => any) extends (拆一个元素: any, ...剩下的数组: infer 剩下的数组类型) => any

? 剩下的数组类型

: [];

//将数字转为对应数组，数组减去一个元素，然后恢复为数字即可。
type 减一<某数 extends number> = 得到长度<数组减一<转为数组<某数>>>;

//汉诺塔关键函数
type 汉诺塔<某数 extends number,塔一,塔二,塔三> = 某数 extends 1

? [塔一,"--->",塔三]
:
[汉诺塔<减一<某数>,塔一,塔三,塔二>,
[塔一,"--->",塔三],
汉诺塔<减一<某数>,塔二,塔一,塔三>]

//渲染
type 测试 = 汉诺塔<3,塔一,塔二,塔三>

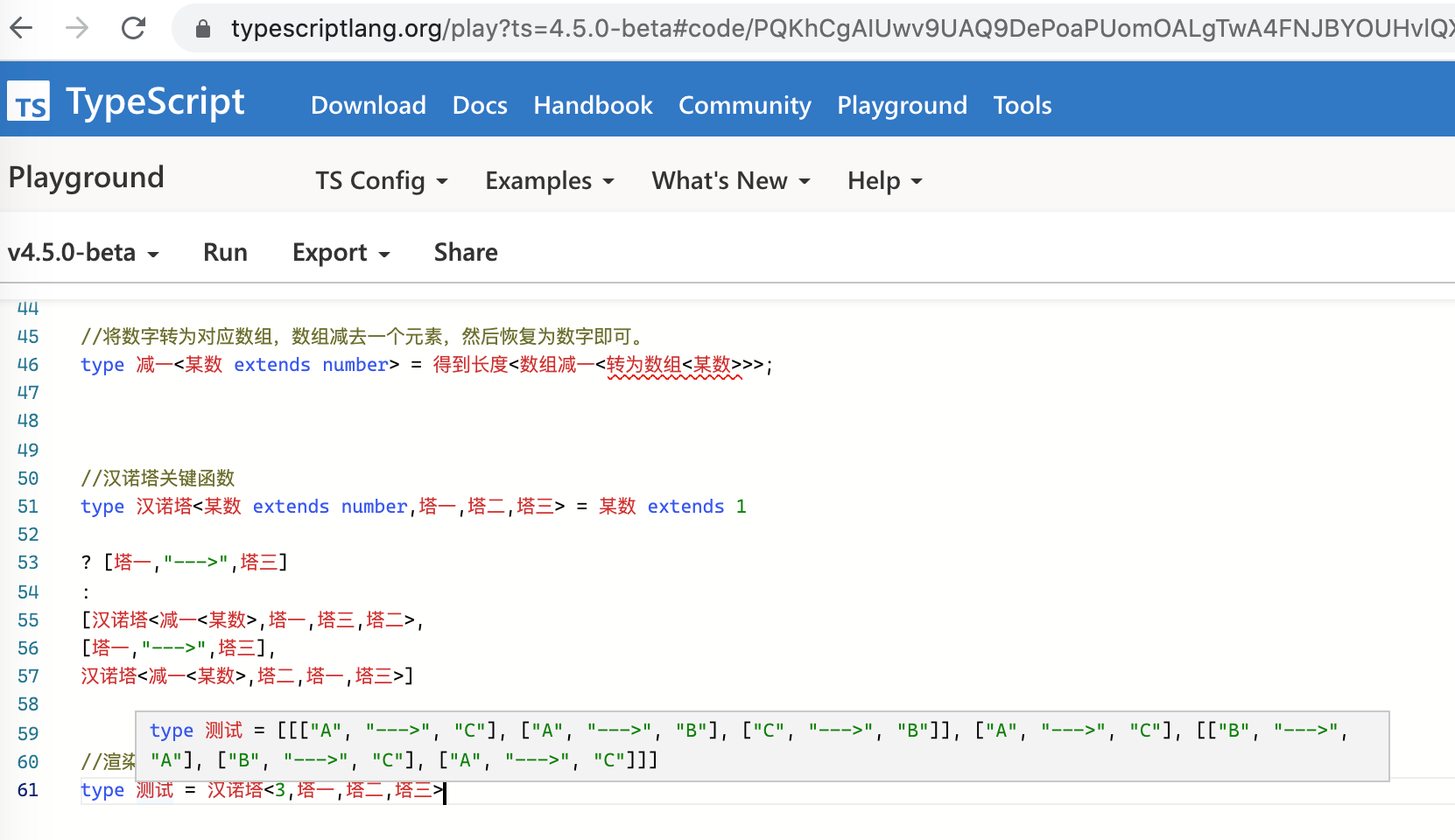
其中还涉及ts相关知识点，详细了解typeScript，不做详细展开说明了。